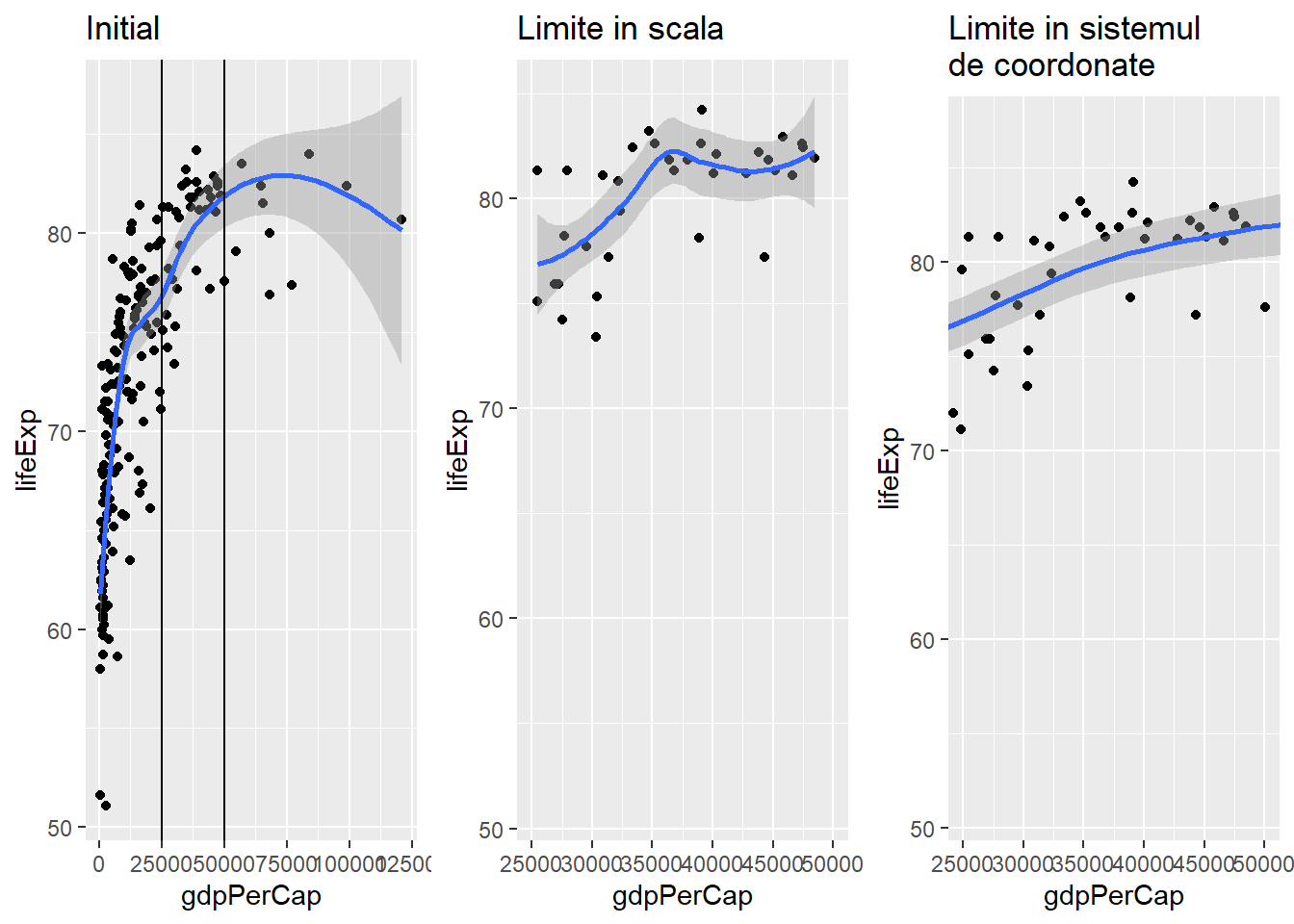
# folosind scala - fitam curba de regresie pe datele ramase
ggplot(gapminder_2018, aes(x = gdpPerCap, y = lifeExp)) +
geom_point() +
geom_smooth() +
scale_x_continuous(limits = c(25000, 50000))
# folosind sistemul de coordonate - fitam curba de regresie
# pe toate datele si evidentiem doar zona de interes
ggplot(gapminder_2018, aes(x = gdpPerCap, y = lifeExp)) +
geom_point() +
geom_smooth()+
coord_cartesian(xlim = c(25000, 50000))Sisteme de coordonate (coordinate systems)
Pachetul ggplot2 pune la dispoziție și o serie de funcții care fac referire la sistemul de coordonate în care sunt trasate elementele grafice. Sistemele de coordonate sunt specificate prin funcții care încep prin coord_ și sunt adăugate ca straturi la graficul existent. Pachetul dispune de mai multe sisteme de coordonate printre care enumerăm:
coord_cartesian- sistemul cartezian care este și cel de default și în care trebuie specificare valorile pe x și ycoord_flip- sistemul cartezian în care axele sunt schimbate între elecoord_fixed- un sistem cartezian care păstrează fixat aspectul (aspect ratio - numărul de unități pe axa y care corespund unei unități pe axa x) cu raportul de bază de 1coord_polar- sistemul de coordonate polarcoord_quickmap- un sistem de coordonate care aproximează sistemul sferic al planeti în vederea trasării hărților
Folosind sistemul cartezian cu opțiunea xlim (respectiv ylim) putem vizualiza doar acea regiune a graficului care ne interesează (putem face zoom). Diferența majoră dintre utilizarea limitelor în interiorul funcției coord_cartesian și utilizarea limitelor în funcțiile de scală (e.g. scale_x_continuous) este că în primul caz utilizăm tot setul de date pe când în cel de al doilea caz sunt folosite doar observațiile care se află între limitele setate, toate celelalte puncte fiind excluse.
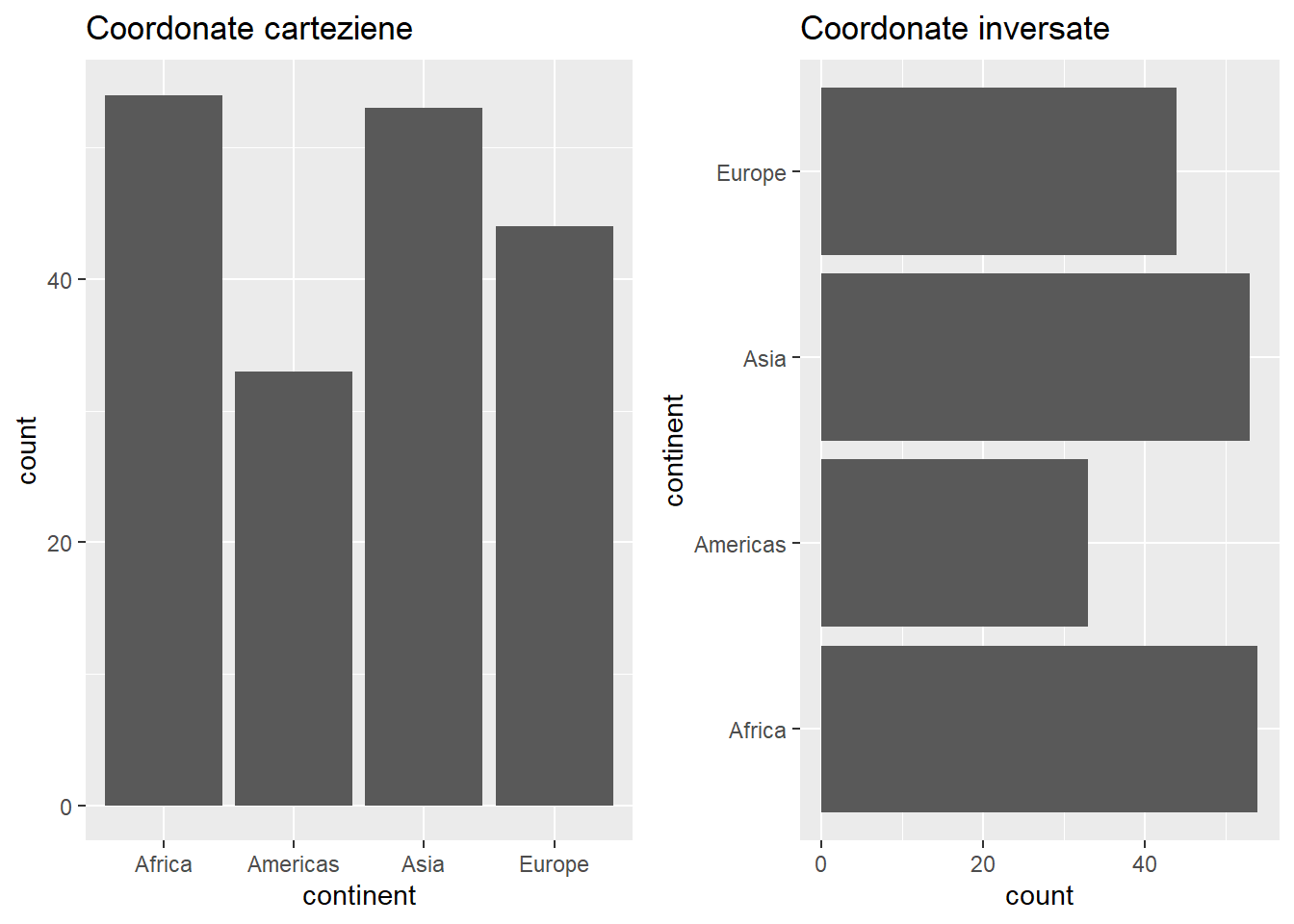
Sunt multe situațiile în care suntem interesați de valorile variabilei de pe axa x condiționate la variabila de pe axa y și în acest caz este recomandată schimbarea (întoarcerea) sistemului de coordonate prin apelarea funcției coord_flip(). De asemenea, o altă situație în care se recomandă rotirea coordonatelor cu 90 de grade este în cazul trasării unei diagrame cu bare sau a unui boxplot în funcție de o variabilă calitativă cu un număr mare de categorii sau cu categorii a căror denumire este lungă. Vom ilustra această transformare a sistemului de coordonate folosind diagrama cu bare pentru a evidenția numărul țărilor din setul de date gapminder_2018 de pe fiecare continent.
# coordonate carteziene
gapminder_2018 %>%
ggplot(aes(x = continent)) +
geom_bar()
# coordonate flip
gapminder_2018 %>%
ggplot(aes(x = continent)) +
geom_bar() +
coord_flip()În mod similar putem vizualiza prin intermediul unui boxplot diferențele dintre duratele medii de viață de pe fiecare continent:
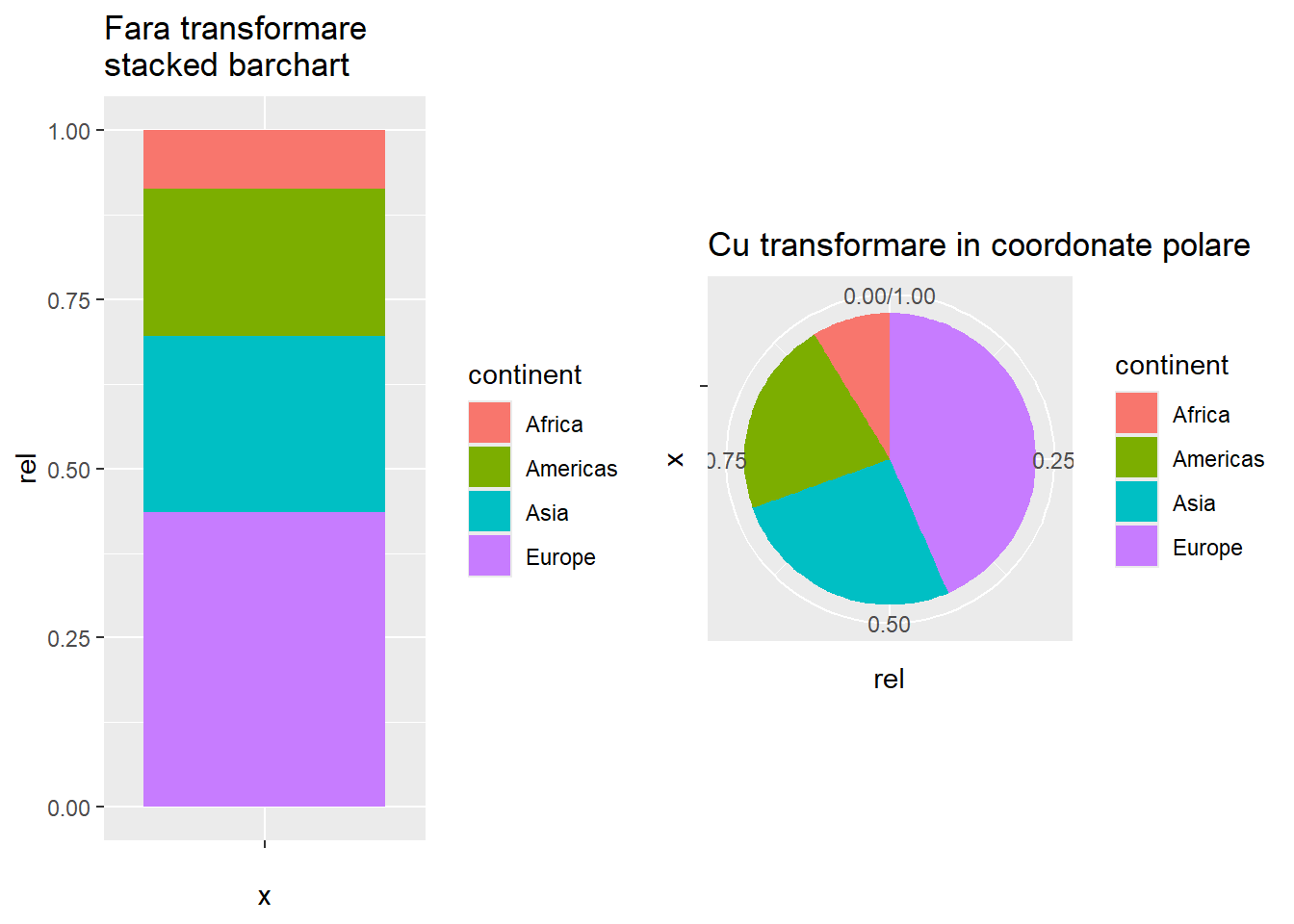
Un alt mod de vizualizare a datelor calitative (categoriale), frecvent utilizat în practică, este reprezentat de diagrama circulară (pie chart). Trebuie menționat că acest tip de grafic nu este recomandat având în vedere că oamenii tind să supraestimeze unghiurile mai mari de 90 de grade și să subestimeze unghiurile mai mici de 90 de grade astfel fiind dificilă compararea mărimii relative a două sectoare din diagrama circulară (robbins2013?). Pentru a crea o diagramă circulară în ggplot2 vom folosi transformarea în coordonate polare coord_polar. Ideea este de a pleca de la o diagramă cu bare suprapuse (stacked barchart) și apoi să o transpunem în coordonate polare.
Figura de mai jos prezintă o diagramă circulară pentru proporția țărilor de pe fiecare continent care depășesc produsul intern brut median global.
gapminder_2018 %>%
mutate(gdp_avg = median(gdpPerCap)) %>%
filter(gdpPerCap > gdp_avg) %>%
mutate(n_all = n()) %>%
group_by(continent) %>%
summarize(rel = n() / unique(n_all)) %>%
ggplot(aes(x = "", y = rel)) +
geom_col(aes(fill = continent)) +
coord_polar("y")Mai multe detalii despre sistemele de coordonate se pot găsi în lucrarea de referință (Wickham 2016).