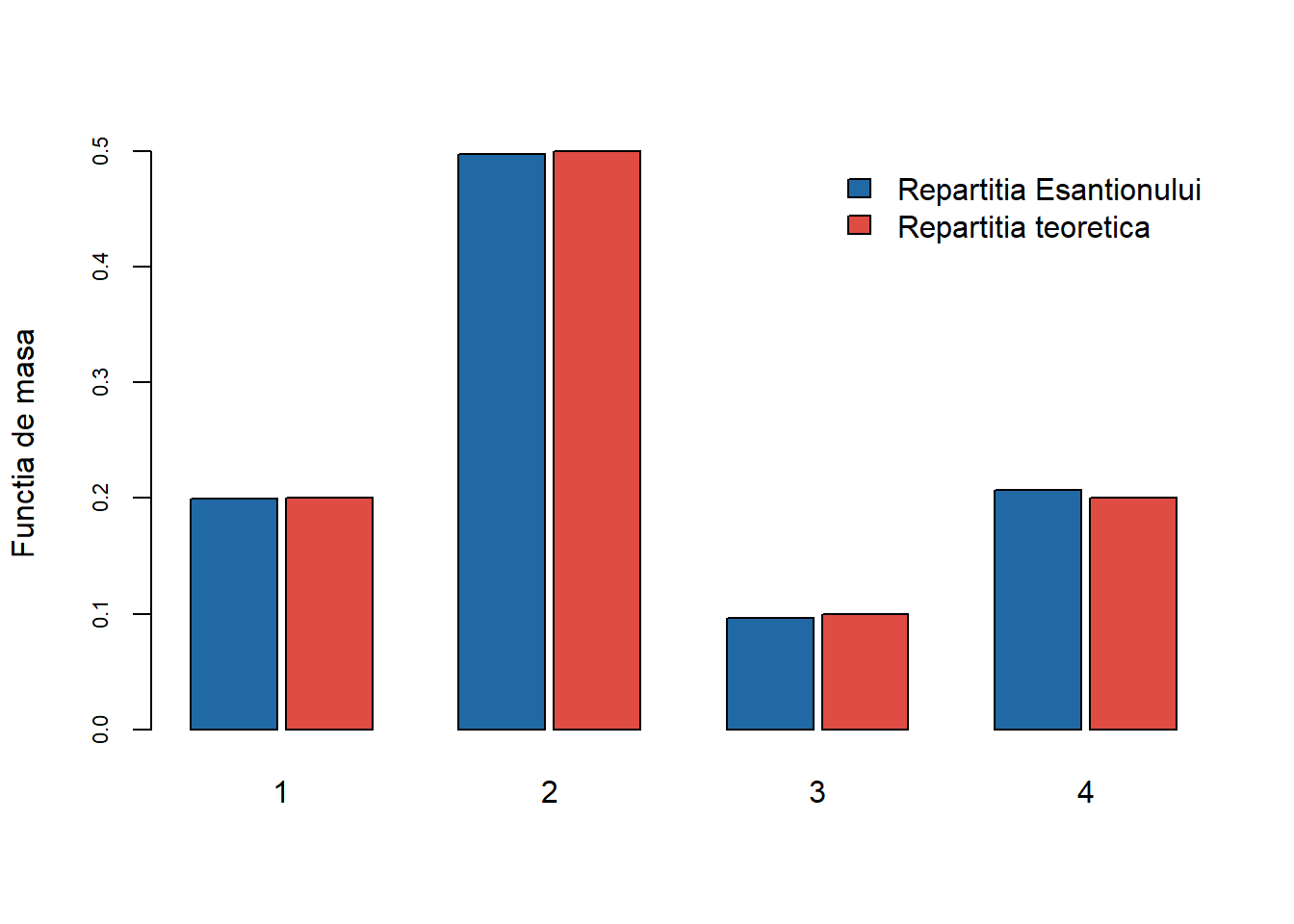l <- seq(10,10000,10)
ll <- length(l)
dat <- data.frame(a = 1:length(l), pi1 = 1:length(l), pi2 = 1:length(l))
for (i in 1:length(l)){
u1 <- runif(l[i])
u2 <- runif(l[i])
v <- runif(l[i])
x <- ifelse(sqrt(u1^2+u2^2)<1,1,0)
y <- sqrt(1-v^2)
dat$pi1[i] <- 4*sum(x)/l[i]
dat$pi2[i] <- 4*sum(y)/l[i]
}
plot(dat$a, dat$pi1,
col = myblue,
xlab = "Volumul esantionului",
ylab = TeX("$\\hat{\\pi}_1$ (albastru) si $\\hat{\\pi}_2$ (rosu)"),
bty = "n",
pch = 16)
points(dat$a, dat$pi2,
col = mygreen,
pch = 16)
abline(h = pi,
lty = 2,
lwd = 3,
col = myred)Scopul acestor note de laborator este de a prezenta succint metodele de simulare introduse la curs și de a le ilustra printr-o serie de exemple în R.
Elemente de simulare
În acest capitol vom prezenta o serie de exemple de generare a observațiilor dintr-o repartiție dată, folosind două metode generale de generare: metoda inversă și metoda respingerii. Înainte de a prezenta metodele de simulare vom ilustra cum putem estima valorile constantelor \(\pi\) și \(e\) aplicând Legea Numerelor Mari (a se vedea Legea Numerelor Mari).
Estimarea constantelor \(\pi\) și \(e\)
În exercițiul de mai jos sunt prezentate două metode de estimare a lui \(\pi\) prin simulare.
Exercițiul 1 Fie \(U_{i1}, U_{i2}, V_{i}\), \(i\in\{1,2,\dots,n\}\), variabile aleatoare independente repartizate uniform \(\mathcal{U}([0,1])\). Definim variabilele aleatoare
\[ X_i=\left\{\begin{array}{ll} 1, & U_{i1}^2+U_{i2}^2<1\\ 0, & \text{altfel} \end{array}\right.\;\;\;\text{și}\;\;\; Y_i=\sqrt{1-V_i^2},\;\; i\in\{1,2,\dots,n\} \]
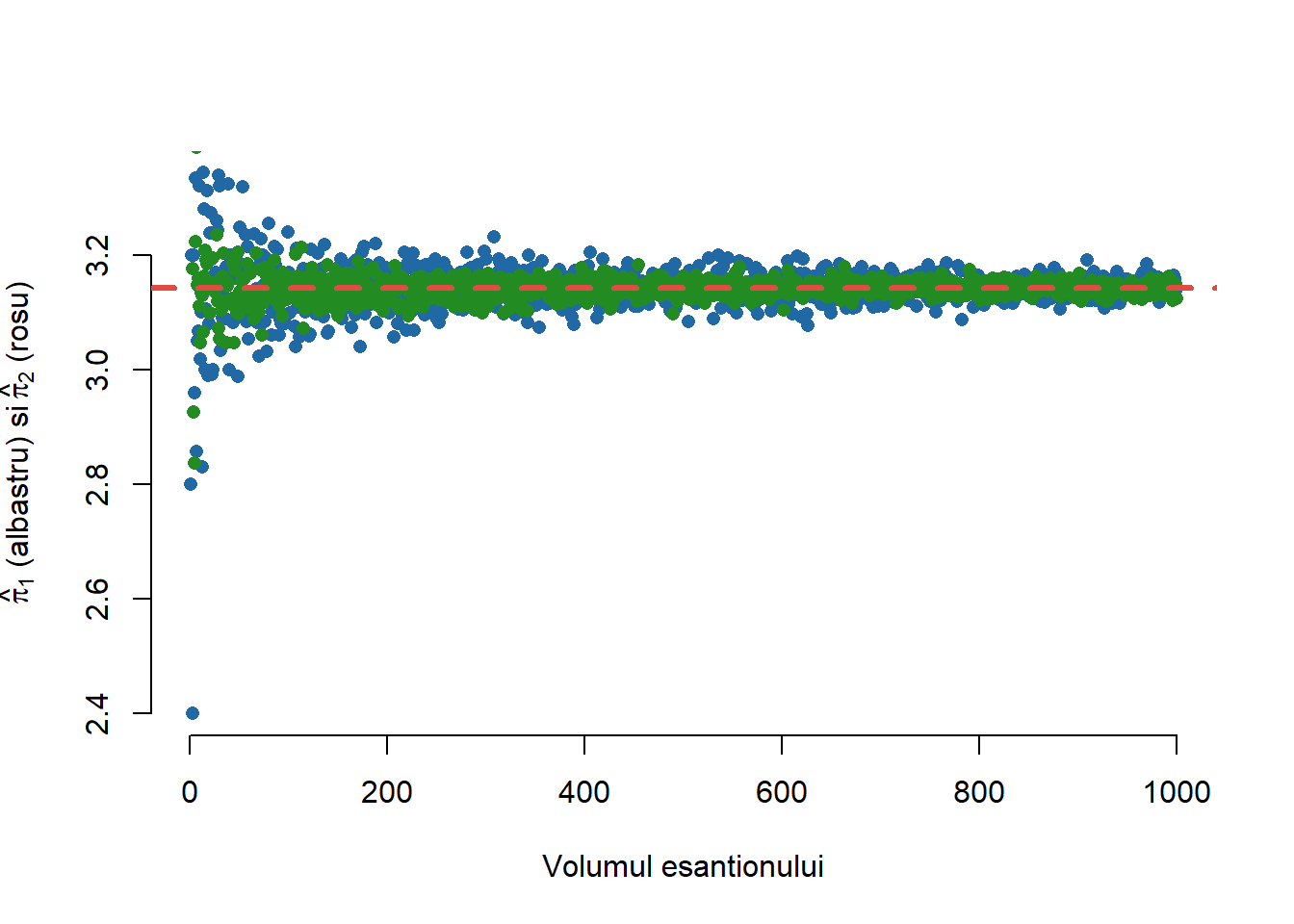
Considerăm variabilele aleatoare \(\hat{\pi}_1=\frac{4}{n}\sum_{i=1}^{n}X_i\) și \(\hat{\pi}_2=\frac{4}{n}\sum_{i=1}^{n}Y_i\). Calculați media și varianța acestor variabile și stabiliți care este mai eficientă1 în estimarea lui \(\pi\).
Soluție. Pentru \(\hat{\pi}_1\): observăm că v.a. \(X_i\) sunt v.a. de tip Bernoulli cu
\[ \begin{aligned} \mathbb{P}(X_i=1)&=\mathbb{P}\left(U_{i1}^2+U_{i2}^2<1\right)=\iint_{\{u^2+v^2<1\}\cap[0,1]^2}f_{(U_{i1},U_{i2})}(u,v)\,dudv \\ &\overset{indep.}{=}\iint_{\{u^2+v^2<1\}\cap[0,1]^2}f_{U_{i1}}(u)f_{U_{i2}}(v)\,dudv\\ &=\int_{0}^{1}\int_{0}^{\sqrt{1-u^2}}1\,dvdu = \int_{0}^{1}\sqrt{1-u^2}\,du\\ &\overset{u=\sin\alpha}{=}\int_{0}^{\frac{\pi}{2}}\cos^2\alpha\,d\alpha=\int_{0}^{\frac{\pi}{2}}\frac{\cos2\alpha+1}{2}\,d\alpha\\ &=\frac{\pi}{4}+\frac{1}{2}\int_{0}^{\frac{\pi}{2}}\cos2\alpha\,d\alpha=\frac{\pi}{4} \end{aligned} \]
O altă variantă de calcul pentru \(\mathbb{P}(X_i=1)\) era să observam că această probabilitate se exprima și ca raportul dintre aria mulțimii \(\{(u,v)\in[0,1]^2\,|,u^2+u^2<1\}\) și cea a pătratului \([0,1]^2\), deci tot \(\frac{\pi}{4}\).
Dacă \(T=\sum_{i=1}^{n}X_i\) atunci \(T\sim\mathcal{B}\left(n,\frac{\pi}{4}\right)\) de unde avem că media este \(\mathbb{E}[T]=\frac{n\pi}{4}\) iar varianța
\[ Var[T]=n\frac{\pi}{4}\left(1-\frac{\pi}{4}\right). \]
Cum \(\hat{\pi}_1=\frac{4}{n}T\) deducem că \(Var[\hat{\pi}_1]=\frac{4\pi-\pi^2}{n}\). Din Legea Numerelor Mari obținem că \(\hat{\pi}_1=\frac{4}{n}\sum_{i=1}^{n}X_i\overset{a.s.}{\to}4\mathbb{E}[X_1]=4\mathbb{P}(X_1=1)=\pi\).
Pentru \(\hat{\pi}_2\), să observăm pentru început că media lui \(Y_1\) este
\[ \mathbb{E}[Y_1] = \int_{0}^{1}\sqrt{1-u^2}\,du = \frac{\pi}{4} \]
iar varianța lui \(Y_1\) este
\[ Var[Y_1] = \mathbb{E}[Y_1^2]-\mathbb{E}^2[Y_1] = \int_{0}^{1}1-u^2\,du -\frac{\pi^2}{16} = \frac{2}{3}-\frac{\pi^2}{16}. \]
Prin aplicarea Legii Numerelor Mari rezultă că
\[ \hat{\pi}_2=\frac{4}{n}\sum_{i=1}^{n}Y_i\overset{a.s.}{\to}4\mathbb{E}[Y_1]=\pi \]
iar varianța lui \(\hat{\pi}_2\) este
\[ Var[\hat{\pi}_2] = \frac{16}{n^2}\sum_{i=1}^{n}Var[Y_i] = \frac{16}{n}\left(\frac{2}{3}-\frac{\pi^2}{16}\right). \]
Pentru a vedea care dintre cei doi estimatori este mai eficient trebuie să verificăm care are varianța mai mică. Cum \(\frac{32}{3}<12<4\pi\) rezultă că \(Var[\hat{\pi}_2]<Var[\hat{\pi}_1]\) deci al doilea estimator este mai eficient.
Figura 1 de mai jos ilustrează acest fenomen:
Următorul exercițiu prezintă o metodă de estimare a lui \(e\) prin simulare și are la bază articolul (Russell 1991).
Exercițiul 2 Fie \(U_1, U_2,\dots, U_n\) variabile aleatoare independente și repartizate \(\mathcal{U}([0,1])\) și \(S_n=\sum_{i=1}^{n}U_i\). Dacă variabila aleatoare \(N\) este definită prin
\[ N = \min\{k\,|\,S_k>1\} \]
atunci:
Arătați că dacă \(0\leq t\leq 1\) atunci \(\mathbb{P}(S_k\leq t) = \frac{t^k}{k!}\).
Determinați \(\mathbb{E}[N]\) și \(Var[N]\).
Soluție. Avem:
- Pentru a calcula probabilitatea \(\mathbb{P}(S_k\leq t)\) cu \(0<t<1\) să ne reamintim că dacă \(X\) și \(Y\) sunt două variabile aleatoare independente cu densitățile \(f_X\) și \(f_Y\) atunci densitatea sumei \(Z = X+Y\) (convoluția) este dată de
\[ f_Z(z) = \int f_X(z-t)f_Y(t)\, dt. \]
Fie \(f_n\) densitatea variabilei aleatoare \(S_n\) pentru \(n\geq1\). Avem, pentru \(0<x<1\), că \(f_1(x) = 1\) și pentru a calcula densitatea \(f_{n+1}\) a variabilei aleatoare \(S_{n+1}\) să observăm că \(S_{n+1} = S_{n} + U_{n+1}\) cu \(S_n\) și \(U_{n+1}\) variabile aleatoare independente, de unde aplicând formula pentru densitatea sumei deducem că
\[ f_{n+1}(x) = \int_{0}^xf_n(t)\,dt, \quad n\geq 1. \]
Prin inducție rezultă că \(f_n(x) = \frac{x^{n-1}}{(n-1)!}\) pentru \(0<x<1\) de unde
\[ \mathbb{P}(S_n\leq t) = \int_{0}^{t}f_n(x)\,dx = \int_{0}^{t}\frac{x^{n-1}}{(n-1)!}\,dx = \frac{t^{n}}{n!}. \]
- Pentru \(n\geq 2\) să observăm că \(\mathbb{P}(N = n) = \mathbb{P}(S_{n-1}<1\leq S_n)\) de unde
\[ \mathbb{P}(N = n) = \mathbb{P}(S_{n-1}<1) - \mathbb{P}(S_n<1) = \frac{1}{(n-1)!} - \frac{1}{n!} = \frac{n-1}{n!}. \]
Pentru medie avem
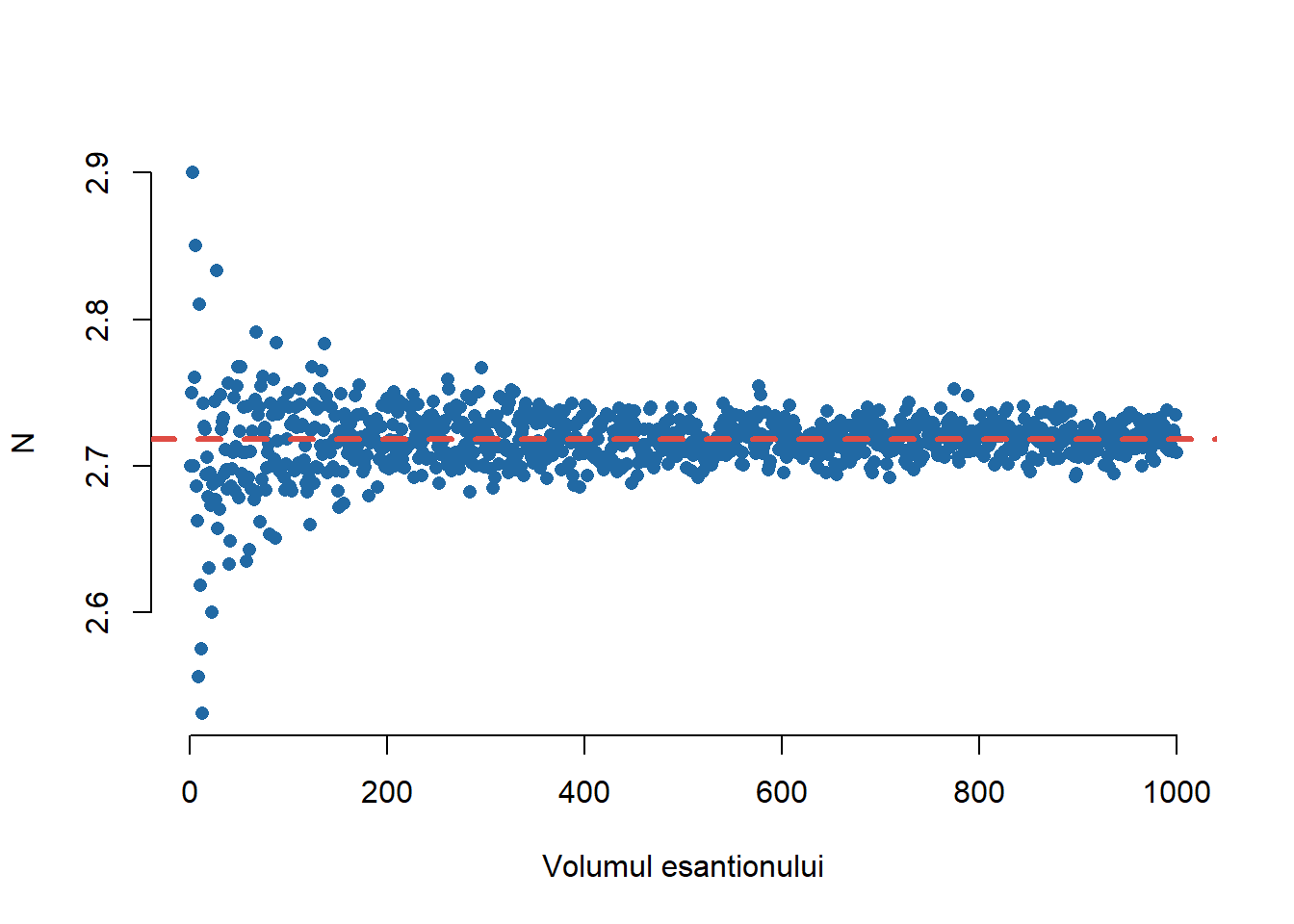
\[ \mathbb{E}[N] = \sum_{n = 2}^{\infty}n\mathbb{P}(N = n) = \sum_{n = 2}^{\infty}n\frac{n-1}{n!} = \sum_{n = 2}^{\infty}\frac{1}{(n-2)!} = e. \]
În mod similar se poate arăta că \(Var[N] = e(3-e)\).2
l <- seq(10,10000,10)
ll <- length(l)
dat <- data.frame(a = 1:length(l), e1 = 1:length(l))
Sime <- function(n){
# genereaza observatii din repartitia N
y <- rep(0, n)
for (i in 1:n){
k <- 1
u <- runif(1)
while(u<1){
u <- u + runif(1)
k <- k+1
}
y[i] <- k
}
return(y)
}
Simev <- Vectorize(Sime, vectorize.args = "n") # vectorize
for (i in 1:length(l)){
x <- Simev(l[i])
dat$e1[i] <- sum(x)/l[i]
}
plot(dat$a, dat$e1,
col = myblue,
xlab = "Volumul esantionului",
ylab = TeX("$N$"),
pch = 16,
bty = "n")
abline(h = exp(1),
lty = 2,
lwd = 3,
col = myred)Generarea variabilelor aleatoare prin metoda inversă
Metoda de simulare prezentată în această secțiune se bazează pe Teorema de universalitate a repartiției uniforme. În esență, rezultatul afirmă că putem genera (cel puțin din punct de vedere teoretic) o observație dintr-o repartiție dată plecând de la o observație uniformă pe \([0,1]\). În practică, acest rezultat este ușor de aplicat atunci când putem determina funcția cuantilă sub formă compactă.
Teorema 1 (Universalitatea Repartiției Uniforme) Fie \(X\) o variabilă aleatoare reală cu funcția de repartiție \(F\), \(U\) o variabilă aleatoare repartizată uniform pe \([0,1]\) și fie funcția cuantilă (inversa generalizată) asociată lui \(F\), \(F^{-1}:(0,1)\to\mathbb{R}\) definită prin
\[ F^{-1}(u) = \inf\{x\in\mathbb{R}\,|\,F(x)\geq u\}, \quad \forall u\in(0,1). \]
Atunci
- Variabilele aleatoare \(X\) și \(F^{-1}(U)\) sunt repartizate la fel.
- Dacă \(F\) este continuă atunci variabila aleatoare \(F(X)\) este repartizată uniform \(\mathcal{U}(0,1)\).
Demonstrație. Avem
- Vom presupune că \(U\sim\mathcal{U}(0,1)\). Cum mulțimile \(\{0\}\) și \(\{1\}\) sunt de măsură Lebesgue nulă, repartiția \(\mathcal{U}(0,1)\) este aceeași cu \(\mathcal{U}((0,1])\), \(\mathcal{U}([0,1))\) sau \(\mathcal{U}([0,1])\). Vrem să arătăm că
\[ \mathbb{P}\left(F^{-1}(U) \leq x\right)=F(x) \]
și ținând cont de funcția de repartiție a variabilei uniforme \(U\sim\mathcal{U}(0,1)\) (\(\mathbb{P}(U \leq F(x))=F(x)\)), aceasta revine la
\[ \mathbb{P}\left(F^{-1}(U) \leq x\right)=\mathbb{P}(U \leq F(x)). \]
Cu alte cuvinte, este suficient să arătăm că evenimentele \(\left\{F^{-1}(U) \leq x\right\}=\{U \leq F(x)\}\) ceea ce este echivalent cu
\[ \forall u \in (0,1), \forall x \in \mathbb{R}, \quad F^{-1}(u) \leq x \Leftrightarrow u \leq F(x). \] Fie \(u \in (0,1)\) și să definim mulțimea \(I_u=\{x \in \mathbb{R} \mid u \leq F(x)\}\). Observăm că \(F^{-1}(u) = \inf I_u\).
Cum \(u<1\) și \(\lim _{x \rightarrow \infty} F(x)=1\) (deoarece \(F\) este funcție de repartiție) deducem că pentru \(x\) suficient de mare avem \(F(x)>u\) prin urmare \(x\in I_u\) de unde \(I_u\neq\emptyset\). Mai mult, dacă \(x\in I_u\) atunci \(F(x)\geq u\) și pentru \(y>x\) avem, din proprietatea de monotonie a funcției de repartiție, că \(F(y)\geq F(x)\) de unde \(y\in I_u\). Astfel obținem că \([x, \infty) \subseteq I_u, \forall x \in I_u\) ceea ce implică că \(I_u\) este un interval de forma \((b, \infty)\) sau \([b,\infty)\).
Presupunem prin absurd că \(b=-\infty\) atunci \(I_u = \mathbb{R}\) și cum \(u>0\) și \(\lim_{x \rightarrow -\infty} F(x)=0\) deducem că pentru \(x\) suficient de mic avem că \(F(x)<u\) de unde \(x \notin I_u\), adică \(I_u \neq \mathbb{R}\), contradicție. Fie acum \(x>b\) atunci \(x \in I_u\) și avem \(F(x)\geq u,\forall x>b\). Cum \(F\) este continuă la dreapta rezultă că
\[ F(b)=\lim _{\substack{x \rightarrow b \\ x>b}} F(x) \geqslant u \Rightarrow b \in I_u \Rightarrow I_u=[b,+\infty) \]
adică \(\inf I_u = b\), dar \(F^{-1}(u) = \inf I_u\) de unde concluzionăm că \(F^{-1}(u) = b\). Astfel am găsit că
\[ F(x) \geqslant u \Leftrightarrow x \in I_{ u } \Leftrightarrow x \geqslant F^{-1}(u). \]
- Fie \(u \in [0,1]\). Vrem să arătăm că \(\mathbb{P}(U\le u)=u\). Observăm că \(F\) este monoton crescătoare, deci pentru orice \(x\) avem \(\{F(x)\le u\} \iff \{x \le F^{-1}(u)\}\) din punctul precedent. Atunci
\[ \mathbb{P}(U\le u)=\mathbb{P}\big(F(X)\le u\big)=\mathbb{P}\big(X\le F^{-1}(u)\big)=F\!\big(F^{-1}(u)\big). \]
Dacă \(F\) este continuă, avem că \(F\!\big(F^{-1}(u)\big)=u\) de unde rezultă
\[ \mathbb{P}(U\le u)=u, \quad u\in[0,1]. \]
Generarea variabilelor aleatoare discrete
În cazul în care \(X\) este o variabilă aleatoare discretă ce ia valori într-o mulțime finită \(X(\Omega)=\{x_1,x_2,\ldots,x_n\}\), unde \(x_1\leq\cdots\leq x_n\), și are funcția de masă \(p_k=\mathbb{P}(X = x_k)\), \(k\in\{1,\ldots,n\}\), putem aplica metoda inversă.
Funcția de repartiție este
\[ F(x) = \left\{\begin{array}{lllll} 0 &,\, x<x_1\\ p_1 &,\, x_1\leq x < x_2\\ p_1 + p_2 &,\, x_2\leq x < x_3\\ & \vdots\\ p_1 + \cdots + p_{n-1} &,\, x_{n-1}\leq x < x_n\\ 1 &,\, x\geq x_n \end{array}\right. = \sum_{i = 1}^{n}(p_1+\cdots+p_{i-1})\mathbf{1}_{[x_{i-1},x_i)}(x), \]
unde \(x_0 = -\infty\) iar \(p_0 = 0\), de unde deducem că funcția cuantilă este
\[ F^{-1}(u) = \left\{\begin{array}{lllll} x_1 &,\, 0 < u \leq p_1\\ x_2 &,\, p_1 < u \leq p_1 + p_2\\ & \vdots\\ x_n &,\, p_1+\cdots+p_{n-1}\leq x \leq 1 \end{array}\right. = \sum_{i=1}^{n}x_i\mathbf{1}_{(p_1+\cdots+p_{i-1}, p_1+\cdots+p_i]}(u). \]
În acest caz putem genera o observație cu repartiția lui \(X\) (\(\mathbb{P}\circ X^{-1}\)) plecând de la \(U(\omega)\), o observație \(\mathcal{U}(0,1)\), și considerând \(Y(\omega) = F^{-1}(U(\omega))\). În practică, este suficient să determinăm indicele unic \(i\) pentru care \(p_1+\cdots+p_{i-1}< U(\omega) \leq p_1+\cdots+p_i\) și să luăm \(Y(\omega) = x_i\).
Trebuie menționat că timpul necesar pentru generarea unei observații este proporțional cu numărul de intervale de tipul \((F(x_{i-1}), F(x_i))]\) pe care le căutăm prin urmare este indicat să ordonăm valorile variabilei aleatoare \(X\) după ordinea descrescătoare a funcției de masă, i.e. după \(p_i\).
În cazul în care \(X(\Omega)\) este numărabilă, rezultatele rămân adevărate numai că trebuie să schimbăm sumele finite cu serii.
Exercițiul 3 Fie \(X\) o variabilă aleatoare cu valori în mulțimea \(\{1,2,3,4\}\). Repartiția \(\nu\) a lui \(X\) este
\[ \mathbb{P}(X = 1) = 0.2, \quad \mathbb{P}(X = 2) = 0.5, \quad \mathbb{P}(X = 3) = 0.1, \quad \mathbb{P}(X = 4) = 0.2. \]
Simulați un eșantion \(u\) de volum \(10000\) de variabile aleatoare i.i.d. repartizate \(\mathcal{U}([0,1])\).
Plecând de la acest eșantion, construiți un eșantion de volum \(10000\), \(x\), de variabile aleatoare i.i.d. repartizate conform \(\nu\).
Comparați, cu ajutorul diagramei cu bare verticale (
barplot), repartiția eșantionului \(x\) și cea teoretică \(\nu\).
Soluție. Avem:
- Pentru a genera observații independente repartizate uniform vom folosi funcția
runif:
n <- 10000
u <- runif(n)- În primul rând să observăm că pentru a genera o variabilă Bernoulli \(\mathcal{B}(1-p)\) este suficient să considerăm variabila \(Y=\mathbf{1}_{\{U>p\}}\) unde \(U\sim\mathcal{U}(0,1)\) care în
Rse scrieas.integer(runif(1)>p)(folosim funcțiaas.integerpentru a transforma un vector logic,runif(1)>p, într-un vector de numere întregi).
Astfel, pentru variabila noastră \(X\) putem scrie
x <- 1 + (u > 0.2) + (u > 0.7) + (u > 0.8)Trebuie remarcat că funcția sample din R permite simularea repartițiilor discrete (e.g. repartiția uniformă pe o mulțime discretă). Pentru exemplul nostru putem să extragem, cu întoarcere, \(n\) numere din mulțimea \(\{1,2,3,4\}\) urmând un vector de probabilități prob:
x <- sample(1:4, n, replace = TRUE,
prob = c(0.2, 0.5, 0.1, 0.2))- Pentru început trebuie să determinăm câte observații sunt din fiecare valoare unică a lui \(x\). Putem face acest lucru folosind funcția
table:
Observăm că eșantionul este repartizat conform \(\nu\).
Următorul exercițiu generalizează rezultatul anterior.
Exercițiul 4 Definiți o funcție care să genereze un eșantion de volum \(n\) dintr-o repartiție discretă definită pe mulțimea \(x=\{x_1,\dots,x_N\}\) (vector numeric sau de caractere) cu probabilitatea \(p=\{p_1,\dots,p_N\}\) pe \(x\).
Soluție. Din punct de vedere practic, pentru a implementa metoda inversă va trebui să reordonăm valorile pe care le poate lua \(X\) în așa fel încât vectorul de probabilități \(p\) să fie descrescător.
Avem următoarea funcție:
GenerateDiscrete <- function(n = 1, x, p, err = 1e-15){
# talia esantionului
# x alfabetul
# p probabilitatile
lp <- length(p)
lx <- length(x)
if(abs(sum(p)-1)>err | sum(p>=0)!=lp){
stop("suma probabilitatilor nu este 1 sau probabilitatile sunt mai mici decat 0")
}else if(lx!=lp){
stop("x si p ar trebui sa aiba aceeasi marime")
}else{
out <- rep(0, n)
indOrderProb <- order(p, decreasing = TRUE) # index
pOrdered <- p[indOrderProb] # rearanjarea probabilitatilor
xOrdered <- x[indOrderProb] # rearanjarea valorilor lui x
u <- runif(n) # generam n uniforme
pOrderedCS <- cumsum(pOrdered)
for (i in 1:n){
# determinam indicele
k <- min(which(u[i]<=pOrderedCS))
out[i] <- xOrdered[k]
}
}
return(out)
}Pentru a testa această funcție să considerăm următoarele două exemple:
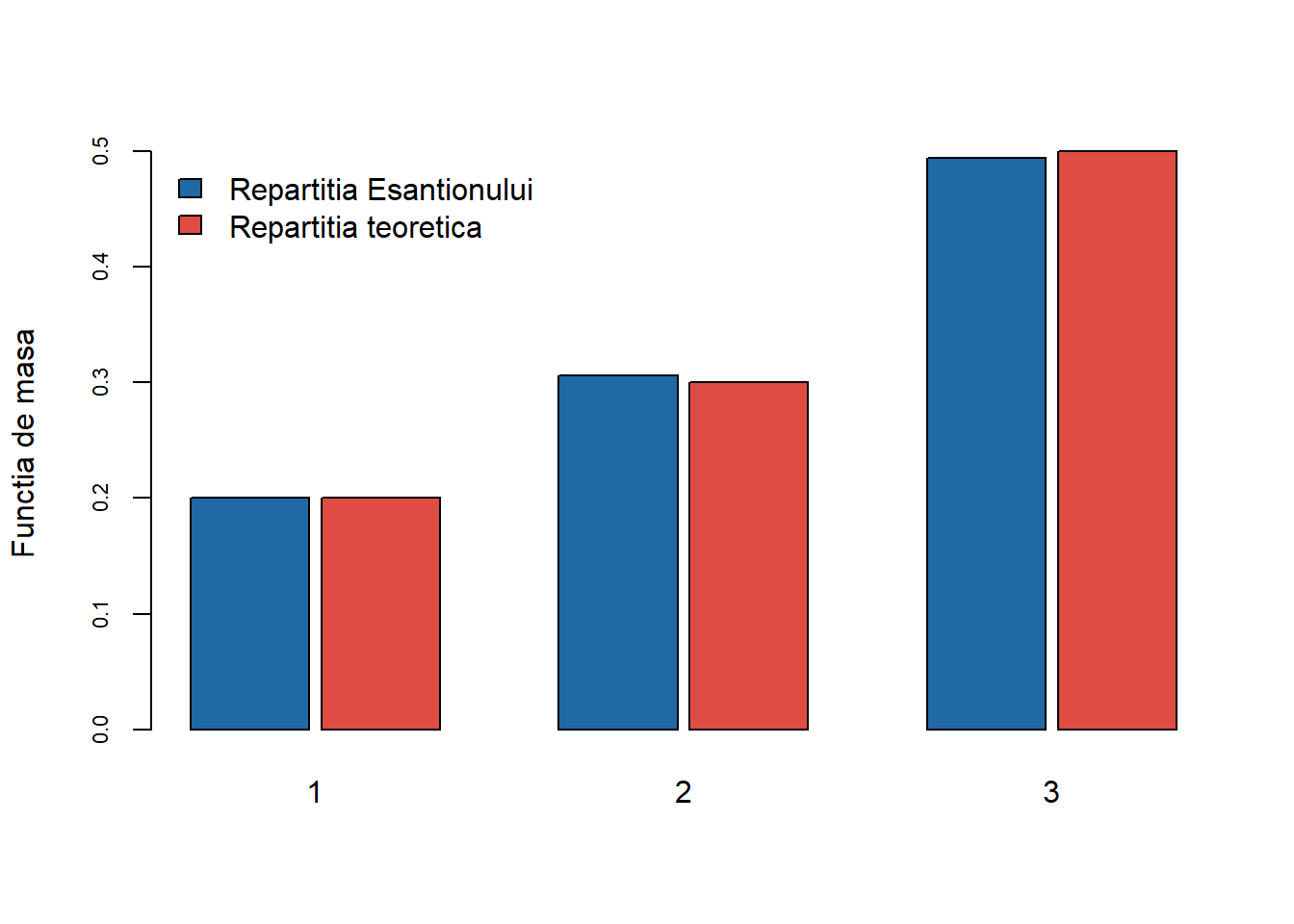
- Ne propunem să generăm observații din \(X\sim\begin{pmatrix}1 & 2 & 3\\ 0.2 & 0.3 & 0.5\end{pmatrix}\), în acest caz: \(x=[1,2,3]\) și \(p=[0.2,0.3,0.5]\). Începem prin generarea a \(n = 10\) observații din repartiția lui \(X\)
GenerateDiscrete(10, c(1,2,3), c(0.2,0.3,0.5)) [1] 1 2 2 1 3 1 3 1 3 3Plecând de la un eșantion de \(n = 10000\) de observații vrem să comparăm, cu ajutorul diagramei cu bare verticale (barplot), repartiția eșantionului cu cea teoretică. Pentru aceasta considerăm următoarea funcție generică:
Compar_diag_bare <- function(pX, pT, legend.loc = "topright",
inset.legend = 0, cex.legend = 1, ...){
indX <- names(pX)
barplot(rbind(pX, pT),
beside = TRUE,
space = c(0.1, 1),
col = c(myblue, myred),
names.arg = indX,
ylab = "Functia de masa",
cex.axis = 0.7,
legend.text = c("Repartitia Esantionului", "Repartitia teoretica"),
args.legend = list(x = legend.loc, bty = "n",
inset = inset.legend, cex = cex.legend), ...)
}Pentru un eșantion de \(n = 10000\) de observații avem:
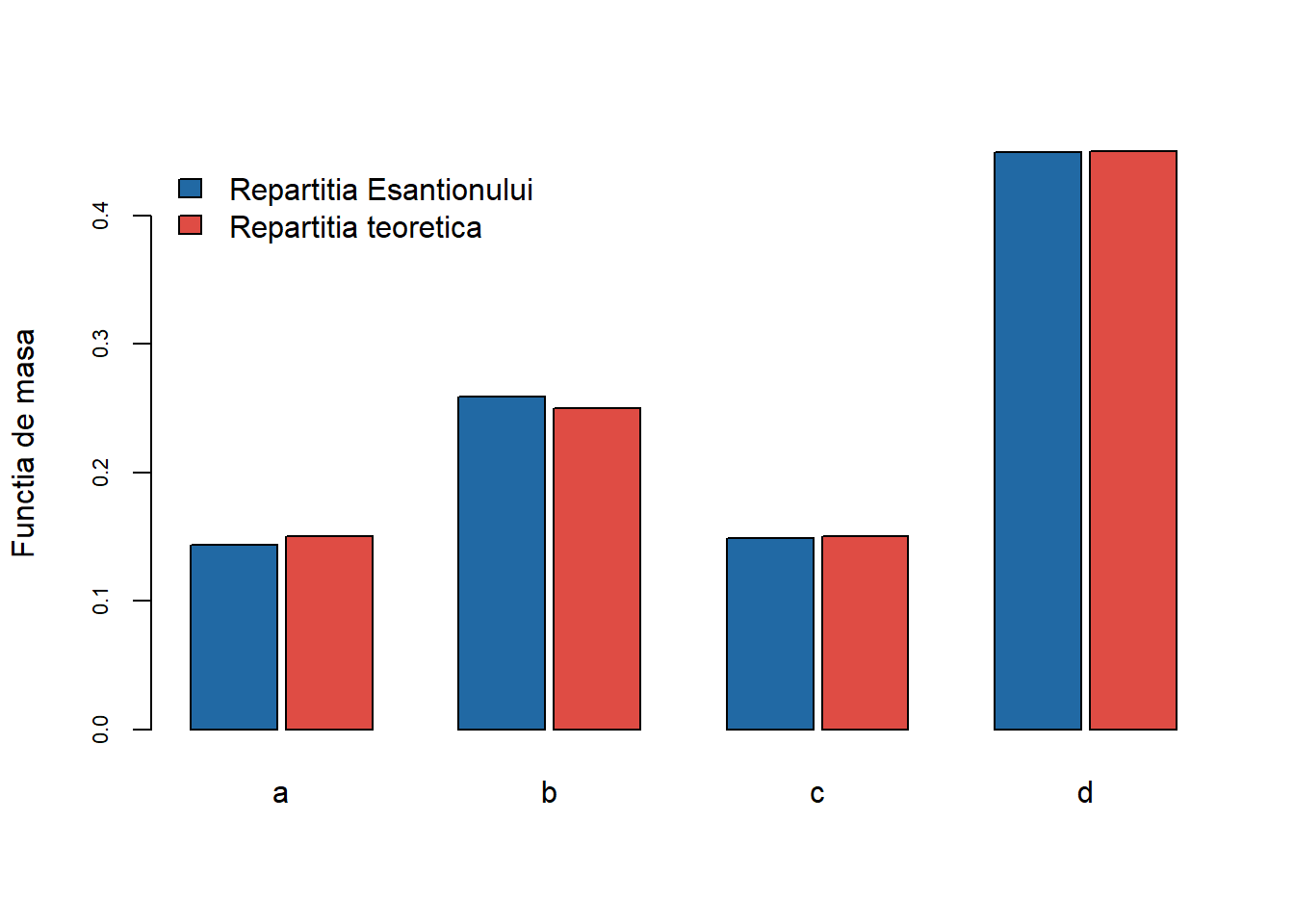
- În acest caz considerăm variabila aleatoare \(X\sim\begin{pmatrix}a & b & c & d\\ 0.15 & 0.25 & 0.15 & 0.45\end{pmatrix}\), deci \(x=[a,b,c,d]\) și \(p=[0.15,0.25,0.15,0.45]\). Mai jos generăm \(n = 15\) observații din repartiția variabilei aleatoare \(X\):
GenerateDiscrete(15, c('a','b','c','d'), c(0.15,0.25,0.15,0.45)) [1] "d" "b" "a" "c" "d" "c" "c" "d" "b" "d" "d" "c" "b" "b" "b"Ca și în cazul primului exemplu, vom compara repartiția teoretică cu cea a unui eșantion de \(n = 10000\) de observații:
În subsecțiunile de mai jos vom testa funcția și pentru o parte din repartițiile discrete de bază: uniformă (discretă), binomială, geometrică, hipergeometrică sau Poisson.
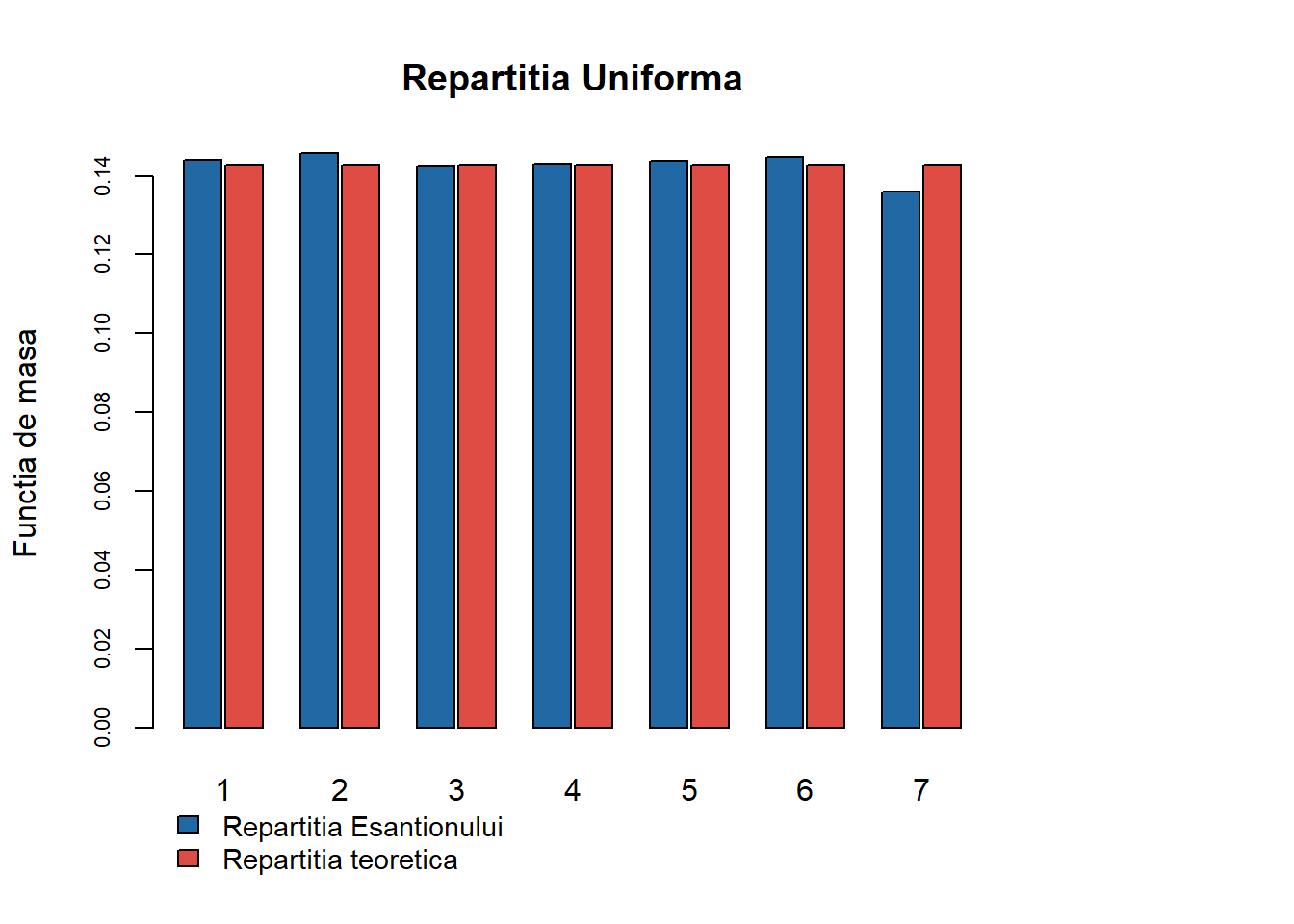
Repartiția Uniformă
În cazul repartiției uniforme pe \(\{1, 2, \ldots, N\}\) (ilustrat mai jos pentru \(N = 7\)) funcția generică conduce la:
Pentru acest caz putem să particularizăm și să găsim un algoritm mai eficient. Ținând cont că funcția de repartiție pentru uniforma pe \(\{1, 2, \ldots, N\}\) este \(F(i) = \frac{i}{N}\) și folosind Teorema de universalitate deducem că
\[ F(i-1) < u \leq F(i) \iff i-1< Nu \leq i \]
cu alte cuvinte \(X\) ia valoarea \(i\) dacă \(i-1< Nu \leq i\) sau altfel spus, dat fiind că \(i\) este întreg, \(i = [Nu] + 1\) adică
\[ X = [Nu] + 1 \]
unde \([x]\) este partea întreagă a lui \(x\). Următoarea funcție implementează această relație:
sim_discrete_unif <- function(n = 100, N = 7){
# n - nr de observatii
# N - uniforme pe 1, 2, ..., N
u <- runif(n)
x <- floor(N*u) + 1
return(x)
}În R putem utiliza funcția sample(1:N, n, replace = TRUE) pentru a genera un eșantion de volum \(n\) din repartiția uniformă pe \(\{1, 2, \ldots, N\}\).
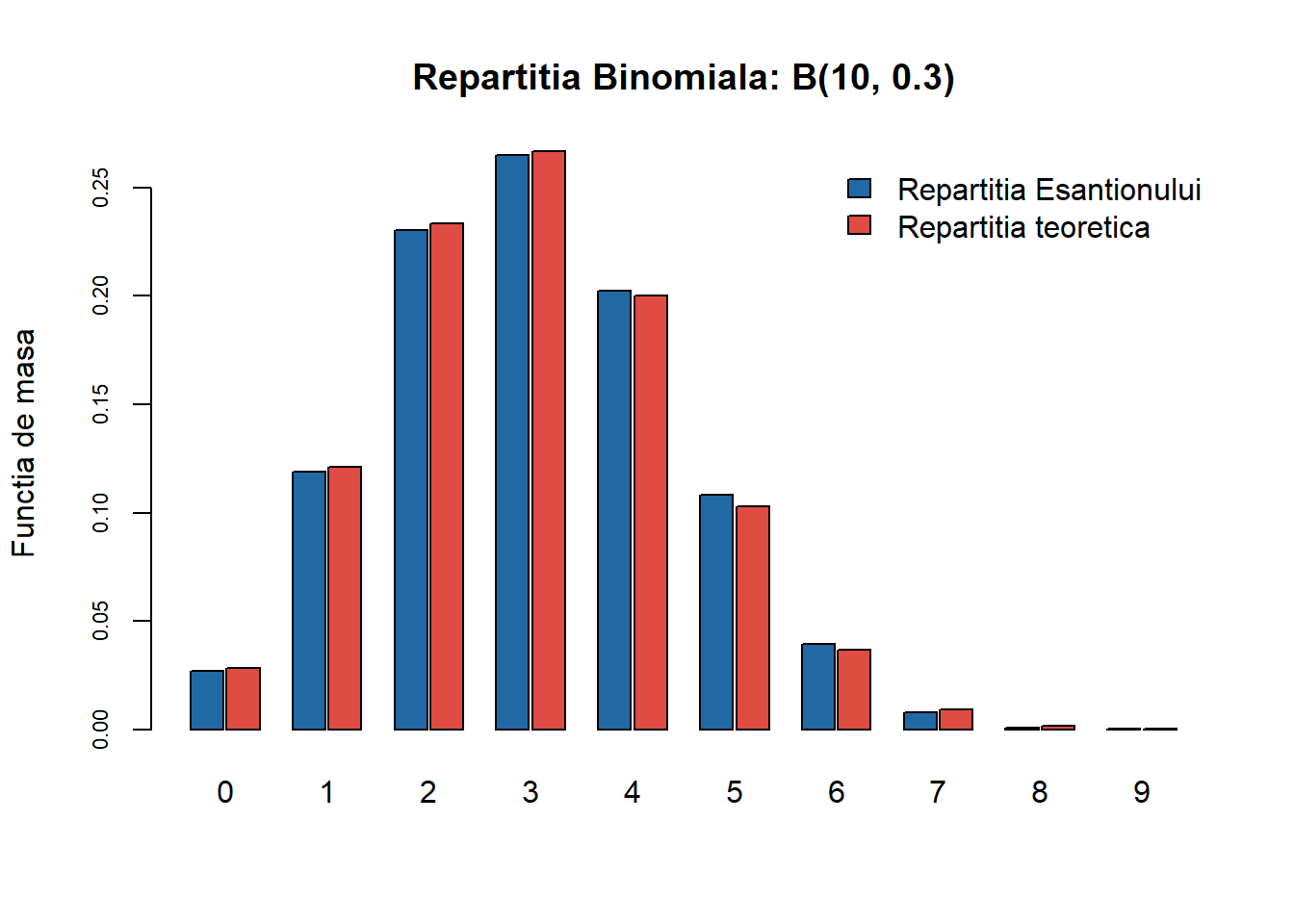
Repartiția Binomială
Vom aplica funcția generică pentru \(\mathcal{B}(10, 0.3)\):
O altă variantă de simulare are la bază calculul funcției de repartiție a \(\mathcal{B}(n,p)\). Ținând cont de relația de recurență
\[ \mathbb{P}(X = i+1) = f(i+1) = \frac{n-i}{i+1}\frac{p}{1-p} f(i), \quad i\geq 1 \]
dintre funcția de masă a \(\mathcal{B}(n,p)\) în \(i+1\) și \(i\), unde \(f(0) = (1-p)^n\) atunci pentru \(u\) o observație uniformă pe \([0,1]\), o observație \(i\) din repartiția \(\mathcal{B}(n,p)\) verifică
\[ \mathbb{P}(X\leq i-1) = F(i-1) < u\leq F(i) = \mathbb{P}(X\leq i) \]
ceea ce conduce la algoritmul
sim_discrete_binom <- function(n = 100, size = 10, p = 0.5){
# n - nr de observatii
# size, p - parametrii binomialei
x <- rep(0, n)
r <- p/(1-p)
for (j in 1:n){
u <- runif(1)
x[j] <- 0
pb <- (1-p)^size
Fr <- pb
while(u >= Fr){
pb <- (size - x[j])/(x[j] + 1) * r * pb
Fr <- Fr + pb
x[j] <- x[j] + 1
}
}
return(x)
}În R putem folosi funcția rbinom() pentru a genera observații repartizate binomial.
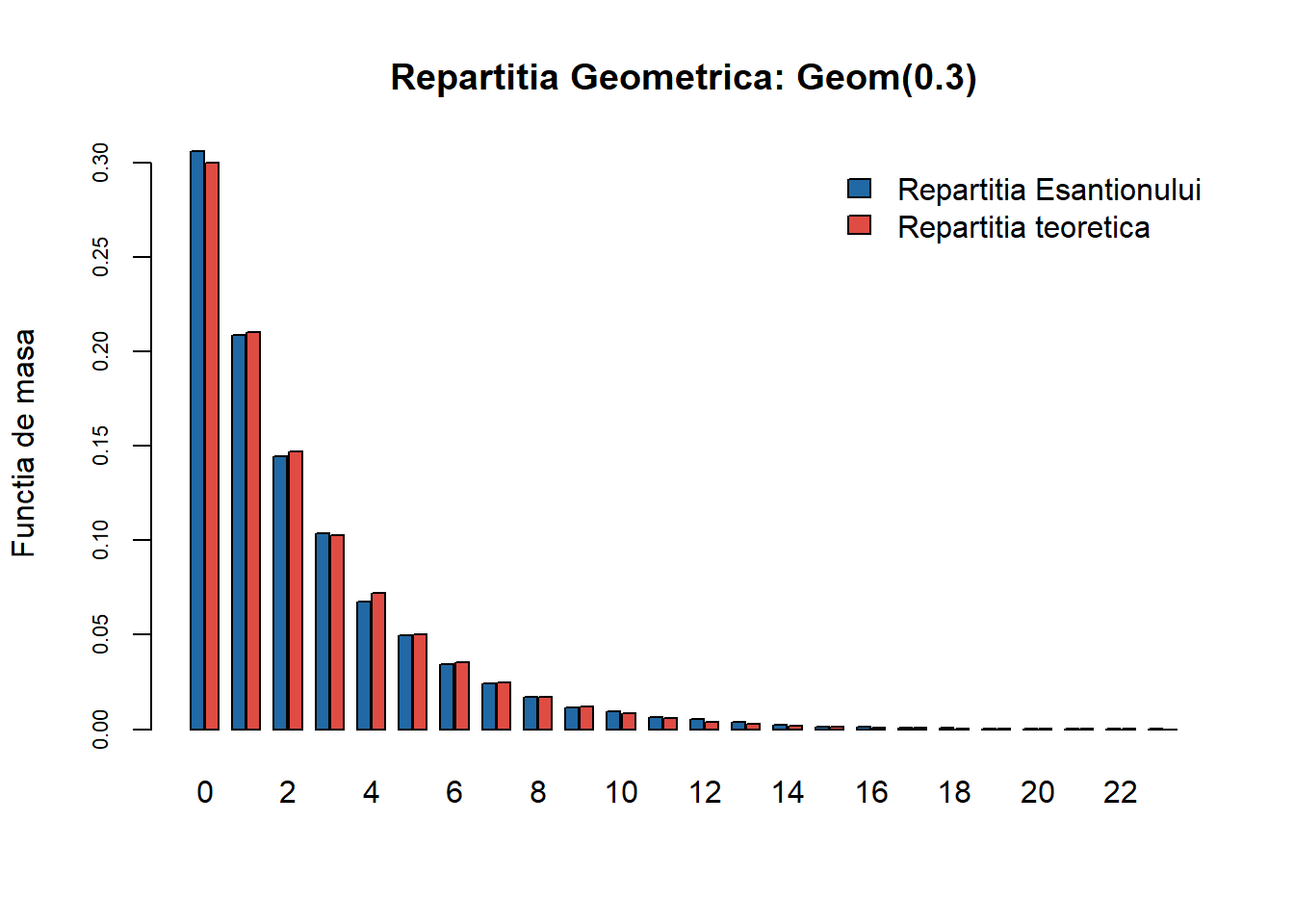
Repartiția Geometrică
Aplicăm funcția GenerateDiscrete pentru \(\mathrm{Geom}(0.3)\) și obținem:
Pentru a îmbunătății algoritmul putem să observăm că în cazul repartiției \(\mathrm{Geom}(p)\) funcția de masă este
\[ \mathbb{P}(X = i) = f(i) = p(1-p)^{i-1}, \quad i\in\{1, 2, \ldots\} \]
ceea ce implică că funcția de repartiție este
\[ F(i) = \sum_{j = 1}^{i}f(j) = 1 - (1-p)^{i-1}. \]
Dacă \(U\sim\mathcal{U}([0,1])\) atunci \(X\) ia valoarea \(i\) care verifică relația \(F(i-1)\leq U< F(i)\) de unde
\[ 1 - (1-p)^{i-1} < U \leq 1 - (1-p)^{i} \iff i< \frac{\log(1-U)}{\log(1-p)} \leq i + 1 \]
ceea ce conduce la \(X = \left[\frac{\log(1-U)}{\log(1-p)}\right]\). Mai mult, pentru \(U\sim\mathcal{U}([0,1])\) avem \(1-U\sim\mathcal{U}([0,1])\) prin urmare \(X = \left[\frac{\log(U)}{\log(1-p)}\right]\). Următoarea funcție implementează acest algoritm:
sim_discrete_geom <- function(n = 100, p = 0.5){
# n - nr de observatii
# p - probabilitatea de succes
u <- runif(n)
x <- floor(log(u)/log(1-p))
return(x)
}În R putem folosi funcția rgeom() pentru a genera observații repartizate geometric.
Repartiția Hipergeometrică
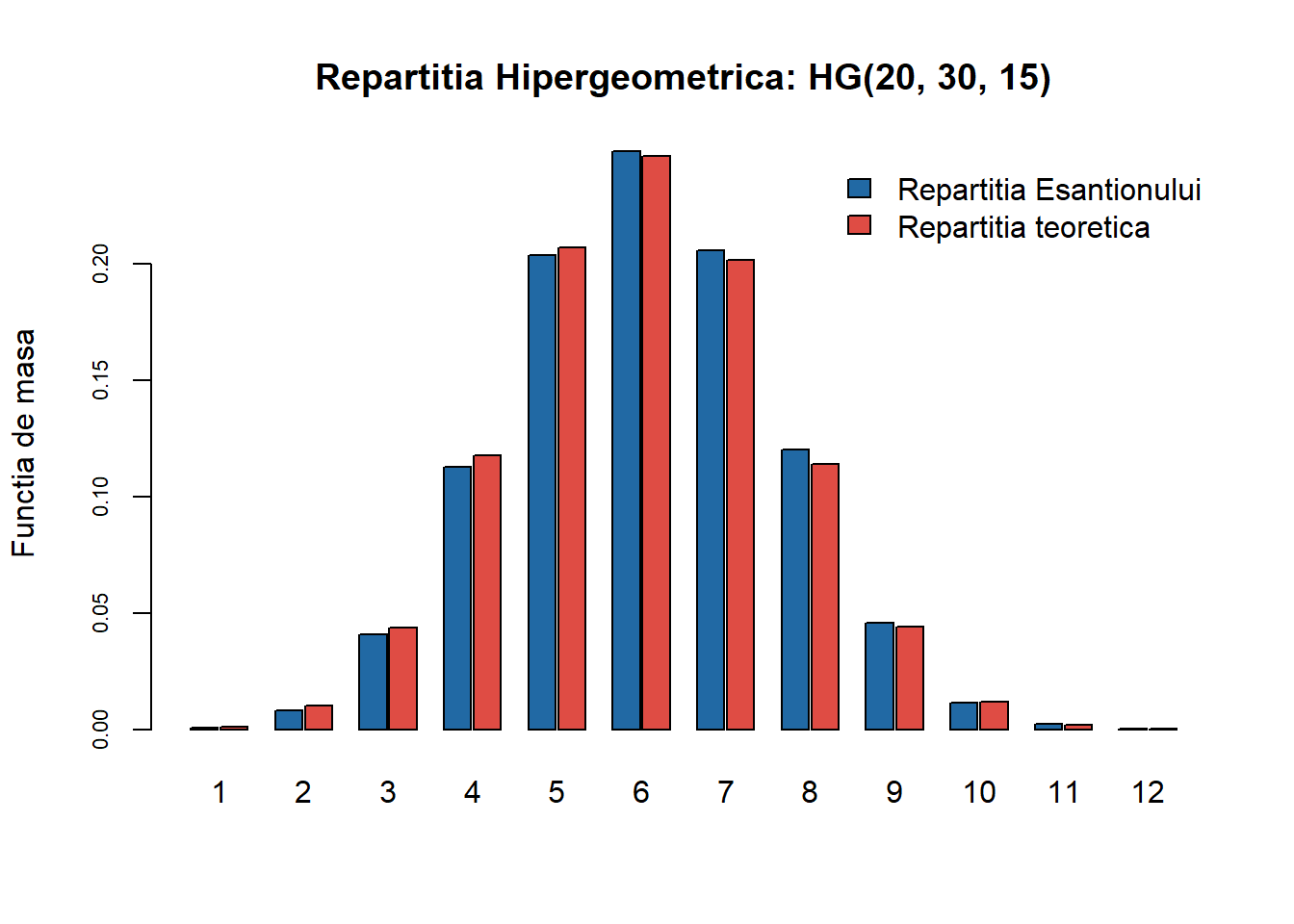
Funcția generică GenerateDiscrete aplicată pentru \(\mathrm{HG}(20,30,15)\) conduce la:
Ca și în cazul repartiției binomiale și după cum vom vedea mai jos a repartiției Poisson, și în cazul repartiției hipergeometrice putem utiliza relația de recurență pentru funcția de masă a \(\mathrm{HG}(n, N, M)\) în punctele \(i+1\) și \(i\). Pentru aceasta trebuie să ținem cont că în R repartiția hipergeometrică primește ca argumente de intrare \(N\) numărul de bile albe (nu numărul total de bile cum am văzut la curs!), \(M\) numărul de bile negre și \(n\) numărul de bile extrase cu întoarcere, i.e. \(\mathrm{HG}(n, N+M, M)\). Astfel funcția de masă devine
\[ \mathbb{P}(X = i) = f(i) = \frac{\binom{M}{i}\binom{N}{n-i}}{\binom{N+M}{n}} \]
iar între \(f(i)\) și \(f(i+1)\) există relația
\[ f(i+1) = \frac{M-i}{i+1}\frac{n-i}{N-n+i+1}f(i), \quad i\geq 0 \]
cu \(f(0)=\frac{\binom{N}{n}}{\binom{N+M}{n}}\). Folosind Teorema de universalitate deducem că pentru \(u\) uniform în \([0,1]\), \(X\) ia valoarea \(i\) care verifică
\[ F(i-1) < u \leq F(i), \]
de unde găsim următorul algoritm:
sim_discrete_hyper <- function(nn = 100, n = 1, N = 10, M = 5){
# nn - nr de observatii generate
# n - nr de bile extrase fara intoarcere
# N - nr de bile albe in urna
# M - nr de bile negre in urna
x <- rep(0, nn)
for (j in 1:nn){
u <- runif(1)
x[j] <- 0
pb <- dhyper(0, M, N, n)
Fr <- pb
while(u >= Fr){
pb <- (M - x[j])/(x[j] + 1) * (n - x[j])/(N - n + x[j] + 1) * pb
Fr <- Fr + pb
x[j] <- x[j] + 1
}
}
return(x)
}În R putem folosi și funcția rhyper() pentru a genera observații repartizate hipergeometric.
Repartiția Poisson
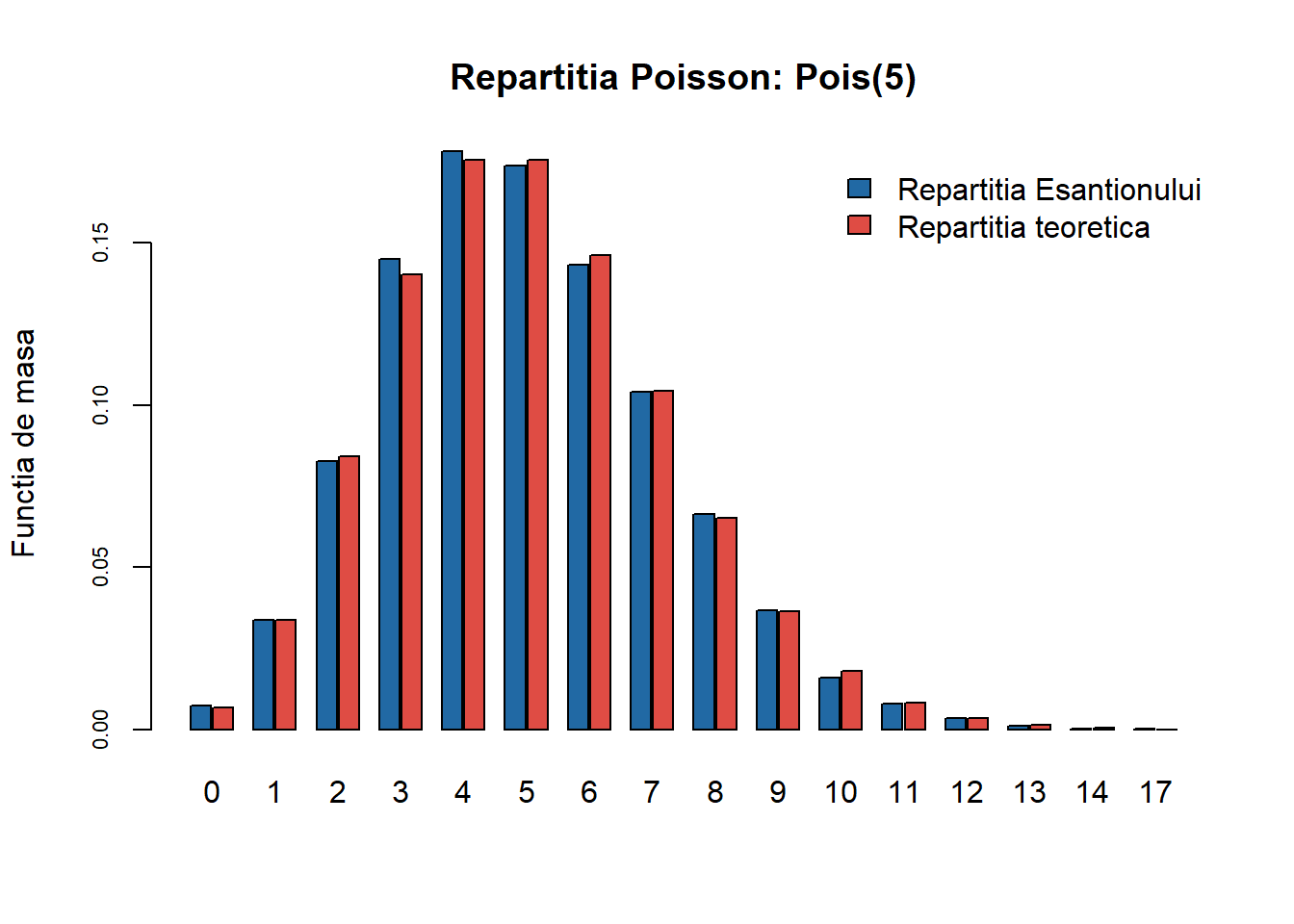
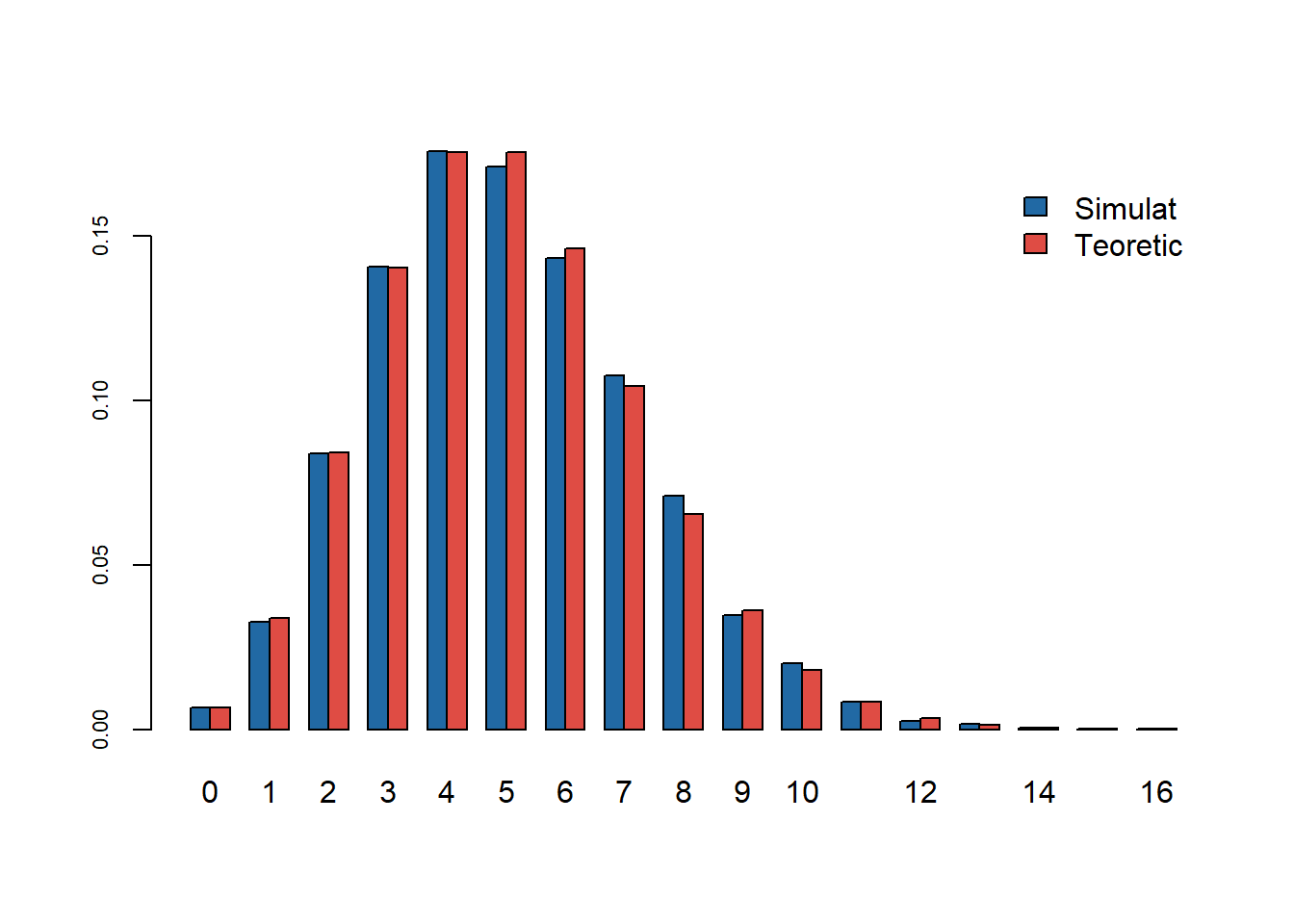
Aplicând funcția GenerateDiscrete pentru \(\mathrm{Pois}(5)\) găsim că:
Reamintim că o variabilă repartizată \(\mathrm{Pois}(\lambda)\) are funcția de masă dată de
\[ \mathbb{P}(X = i) = f(i) = e^{-\lambda}\frac{\lambda^i}{i!},\quad i\geq 0. \]
O metodă mai eficientă de simulare combină rezultatul din Teorema de universalitate și relația de recurență pentru funcția de masă următoare
\[ f(i+1) = \frac{\lambda}{i+1}f(i),\quad i\geq 0, \quad f(0) = e^{-\lambda}. \]
Astfel, pentru \(u\) o observație uniformă pe \([0,1]\), o observație \(i\) din repartiția \(\mathrm{Pois}(\lambda)\) verifică
\[ \mathbb{P}(X\leq i-1) = F(i-1) < u \leq F(i) = \mathbb{P}(X\leq i) \]
ceea ce conduce la algoritmul
sim_discrete_pois1 <- function(n = 100, lambda = 1){
# n - nr de observatii
# lambda - media Poisson
x <- rep(0, n)
for (j in 1:n){
u <- runif(1)
x[j] <- 0
p <- exp(-lambda)
Fr <- p
while(u >= Fr){
p <- p*lambda/(x[j] + 1)
Fr <- Fr + p
x[j] <- x[j] + 1
}
}
return(x)
}O altă modalitate de generare a observațiilor din repartiția \(\mathrm{Pois}(\lambda)\) este dată în Secțiunea 0.5.1. Totodată, în R putem folosi și funcția rpois() pentru a genera observații repartizate Poisson.
Generarea variabilelor aleatoare continue
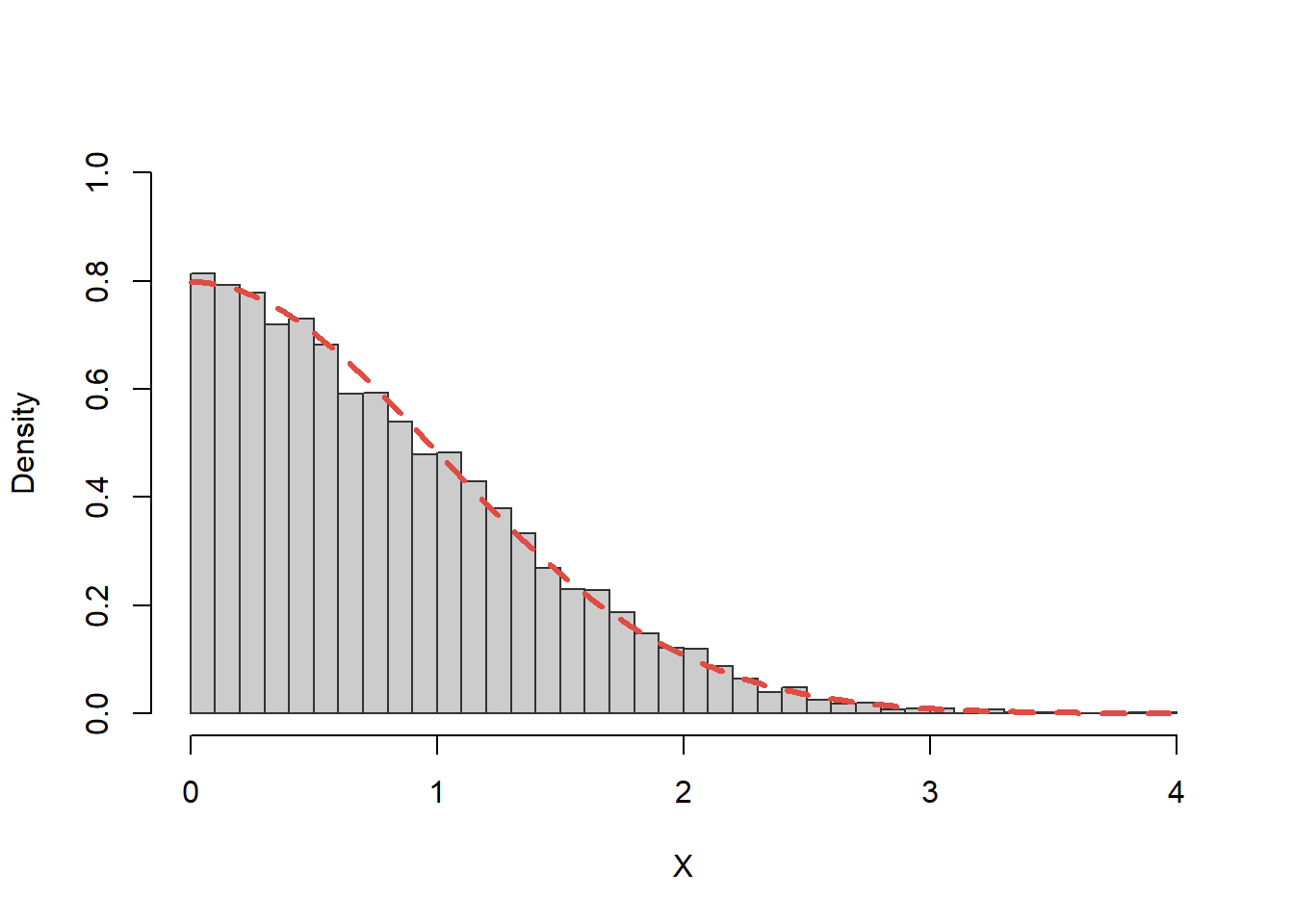
Exercițiul 5 Scrieți un program care să folosească metoda transformării inverse pentru a genera \(n\) observații din densitatea
\[ f(x) = \left\{\begin{array}{ll} \frac{1}{x^2}, & x\geq 1\\ 0, & \text{altfel} \end{array}\right. \]
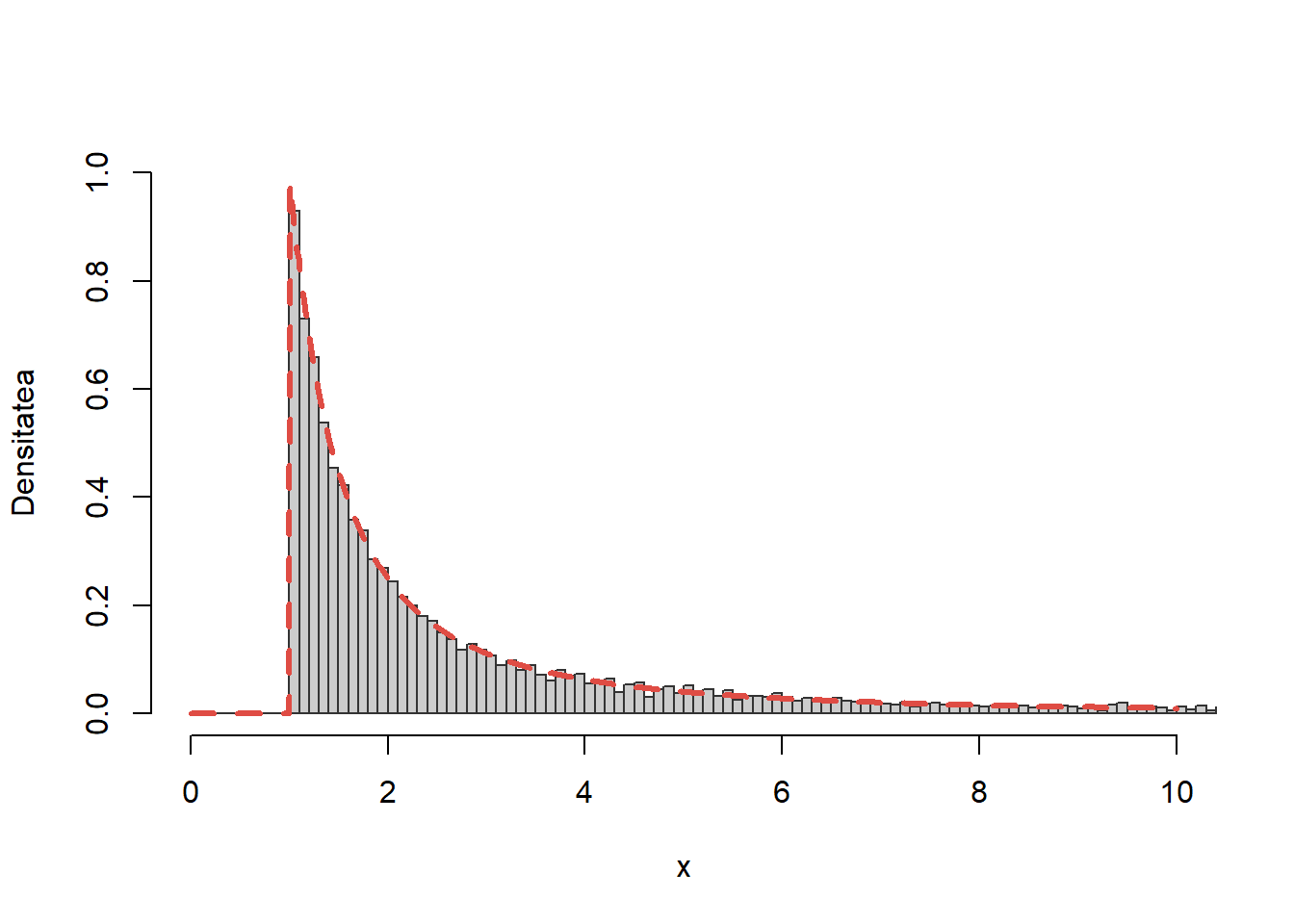
Testați programul trasând o histogramă a \(10000\) de observații aleatoare împreună cu densitatea teoretică \(f\).
Soluție. Primul pas este să determinăm funcția de repartiție \(F\) corespunzătoare acestei densități. Pentru \(x<1\) avem că \(f(x)=0\) deci \(F(x)=0\) iar pentru \(x\geq 1\) avem
\[ F(x) = \int_{1}^{x}\frac{1}{t^2}\, dt = 1 - \frac{1}{x}. \]
Cum \(F\) este continuă putem să determinăm \(F^{-1}\) rezolvând ecuația \(F(x)=u\). Un calcul direct conduce la \(F^{-1}(u)=\frac{1}{1-u}\) și aplicând Teorema de universalitate găsim că \(X = \frac{1}{1-U}\) cu \(U\sim \mathcal{U}([0,1])\).
Astfel putem simula un eșantion de volum \(n\) din populația \(f\) construind funcția
sim_f <- function(n){
u <- runif(n)
return(1/(1-u))
}Pentru a testa comparăm valorile simulate cu densitatea teoretică
Repartiția Exponențială
Exercițiul 6 Scrieți o funcție care să folosească metoda transformării inverse pentru a genera \(n\) observații dintr-o repartiție \(\mathrm{Exp}(\lambda)\).
Soluție. Reamintim că o variabilă aleatoare \(X\sim\mathrm{Exp}(\lambda)\) dacă admite o densitate de repartiție de forma
\[ f(x) = \lambda e^{-\lambda x}\mathbb{1}_{\mathbb{R}_+}(x),\quad \forall x\in\mathbb{R}. \]
Pentru a aplica Teorema de uniersalitate va trebui să determinăm funcția cuantilă. Știm că funcția de repartiție a repartiției exponențiale este
\[ F(x) = (1 - e^{-\lambda x})\mathbb{1}_{\mathbb{R}_+}(x), \quad x\in \mathbb{R} \]
ceea ce conduce la
\[ F^{-1}(u) = -\frac{1}{\lambda}\log(1-u), \quad u\in [0,1]. \]
Astfel putem genera o variabilă aleatoare \(X\) repartizată \(\mathrm{Exp}(\lambda)\), generând \(U\sim\mathcal{U}([0,1])\) și, ținând seama că și \(1-U\sim\mathcal{U}([0,1])\), luând
\[ X = -\frac{1}{\lambda}\log(U). \]
Următorul cod implementează funcția din enunțul exercițiului:
sim_cont_exp <- function(n, lambda){
# n - nr de observatii
# lambda - parametrul repartitiei Exponentiale
u <- runif(n)
x <- -log(u)/lambda
return(x)
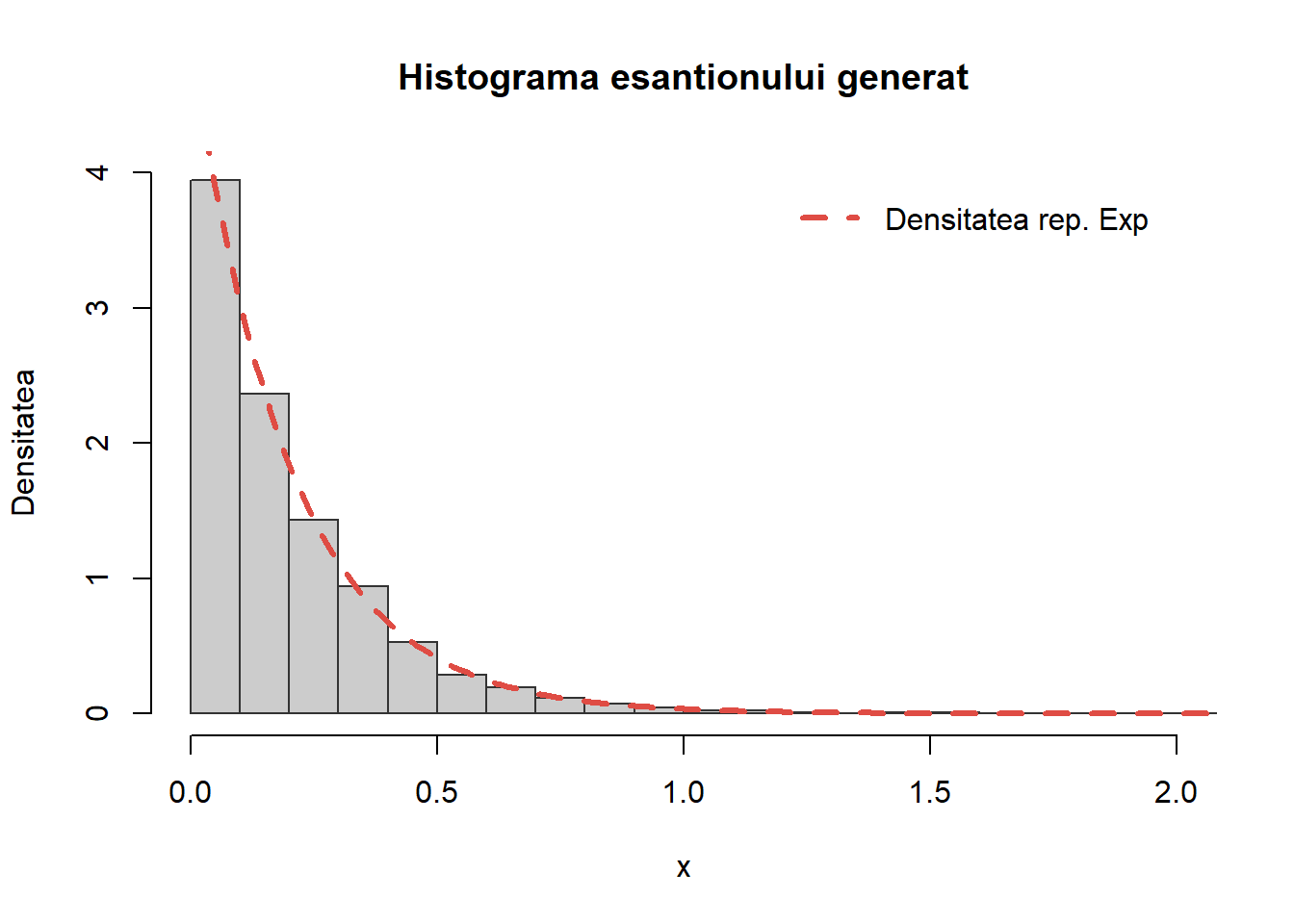
}Pentru a testa comparăm valorile simulate cu densitatea teoretică
Să observăm că în R putem folosi funcția rexp(n, rate = ...) pentru generarea de observații repartizate exponențial.
Repartiția Gamma
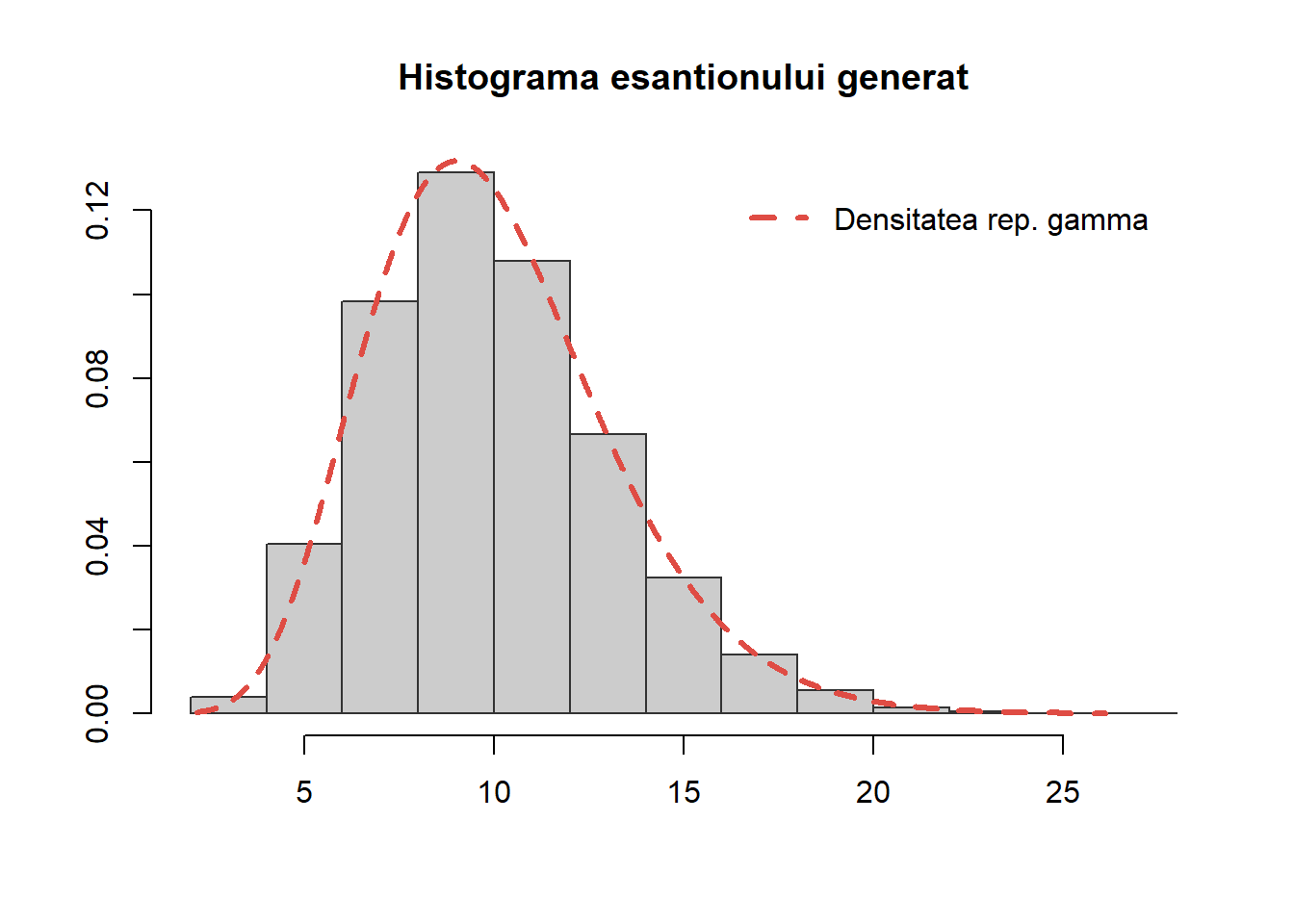
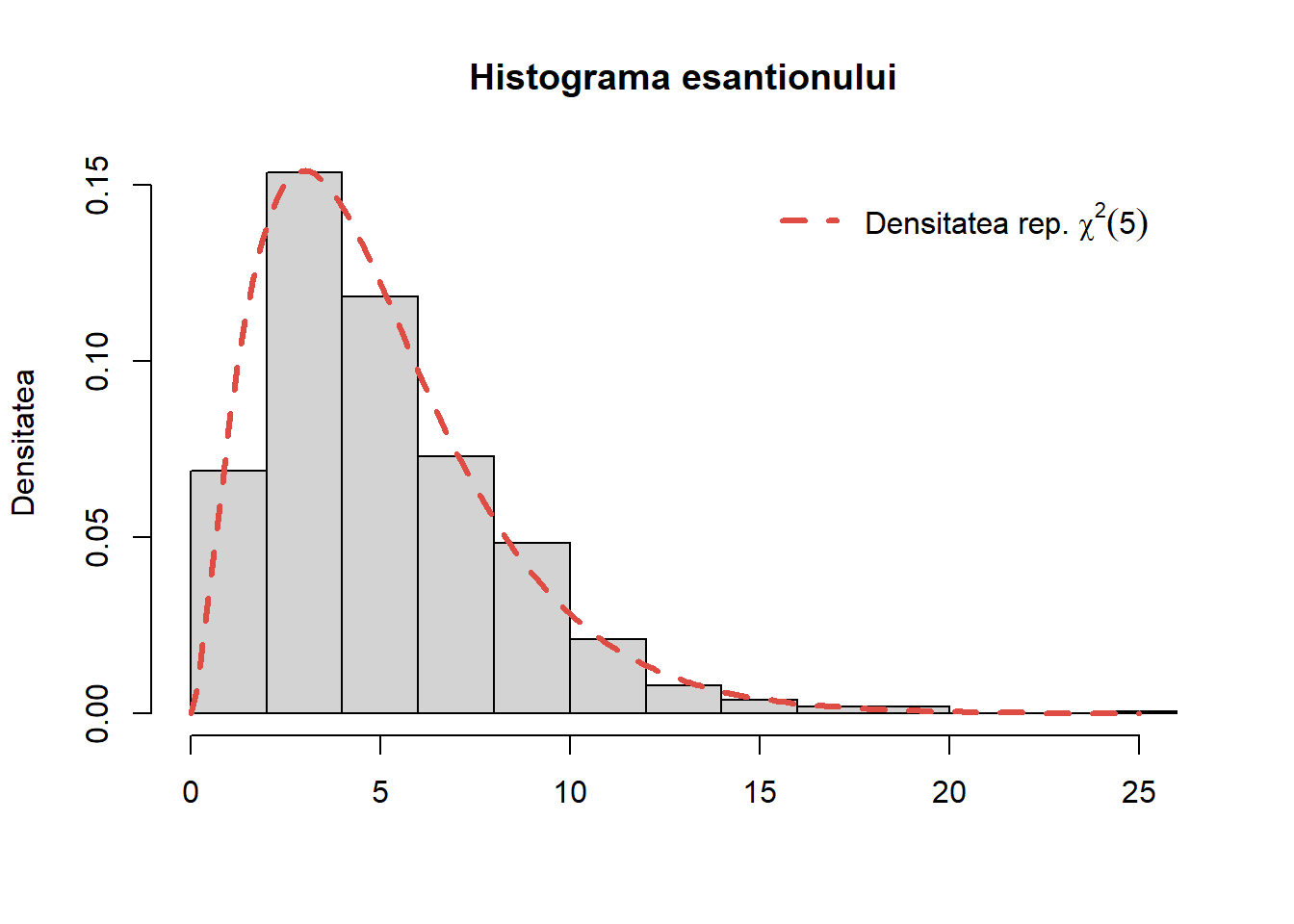
Exercițiul 7 Fie \(X_1, \ldots, X_n\), \(n\) variabile aleatoare i.i.d. repartizate \(\mathcal{E}(\lambda)\). Atunci variabila aleatoare \(S_n = X_1 + X_2 +\cdots+ X_n\) este repartizată \(\Gamma(n, \lambda)\). Plecând de la acest rezultat, generați \(10000\) de observații din repartiția \(\Gamma(n, \lambda)\) (\(n = 10\)). Trasați histograma acestui eșantion și comparați cu densitatea repartiției.
Soluție. Faptul că \(X_1 + X_2 +\cdots+ X_n\sim\Gamma(n, \lambda)\) este arătat în Exercițiul 20. Pentru generarea a \(m\) variabile aleatoare i.i.d. repartizate \(\Gamma(n, \lambda)\), simulăm \(m\times n\) variabile repartizate exponențial pe care le stocăm într-o matrice cu \(m\) linii și \(n\) coloane. Suma elementelor de pe o linie reprezintă o realizare a repartiției \(\Gamma(n, \lambda)\).
sim_cont_gamma <- function(m, n, lambda = 1){
out <- rowSums(matrix(sim_cont_exp(m * n, lambda), m, n))
return(out)
}Din punct de vedere al costului de memorie, această metodă poate să nu fie optimă. Putem folosi o abordare mai simplă folosind bucla for:
sim_cont_gamma2 <- function(m, n, lambda = 1){
out <- numeric(m)
for (i in 1:m){
out[i] <- sum(sim_cont_exp(n, lambda))
}
return(out)
}Pentru verificare considerăm repartiția \(\Gamma(10,1)\) și avem
În R putem folosi funcția rgamma(n, ...) pentru generarea de observații repartizate Gamma.
Repartiția Weibull
Exercițiul 8 Scrieți o funcție care să folosească metoda transformării inverse pentru a genera \(n\) observații dintr-o repartiție Weibull \(\mathrm{Weib}(\alpha, \beta)\).
Soluție. Spunem că o variabilă aleatoare \(X\) este repartizată Weibull de parametrii \(\alpha>0\) și \(\beta>0\), notat \(X\sim\mathrm{Weib}(\alpha, \beta)\), dacă admite ca densitate de repartiție pe
\[ f(x) = \frac{\alpha}{\beta}\left(\frac{x}{\beta}\right)^{\alpha-1}e^{-\left(\frac{x}{\beta}\right)^{\alpha}}\mathbf{1}_{[0,\infty)}(x). \]
Funcția de repartiție este dată de
\[ F(x) = \int_0^x \frac{\alpha}{\beta}\left(\frac{x}{\beta}\right)^{\alpha-1} \exp \left(-\left(\frac{t}{\beta}\right)^\alpha\right) \mathrm{d} t = 1-e^{ -\left(\frac{x}{\beta}\right)^\alpha}\mathbf{1}_{[0,\infty)}(x) \]
iar un calcul simplu conduce la funcția cuantilă
\[ F^{-1}(u) = \beta(-\log (1-u))^{1 / \alpha}. \]
Astfel pentru a genera \(X\sim\mathrm{Weib}(\alpha, \beta)\), considerăm \(U\sim\mathcal{U}([0,1])\) și, ținând cont de \(1-U\sim\mathcal{U}([0,1])\), luăm
\[ X = \beta(-\log (U))^{1 / \alpha}. \]
Următoarea funcție implementează această procedură:
sim_cont_weib <- function(n = 1, alpha = 1, beta = 1){
# n - nr de obs
# alpha - parametrul de forma
# beta - parametrul de scala
u <- runif(n)
x <- beta*(-log(u))^(1/alpha)
return(x)
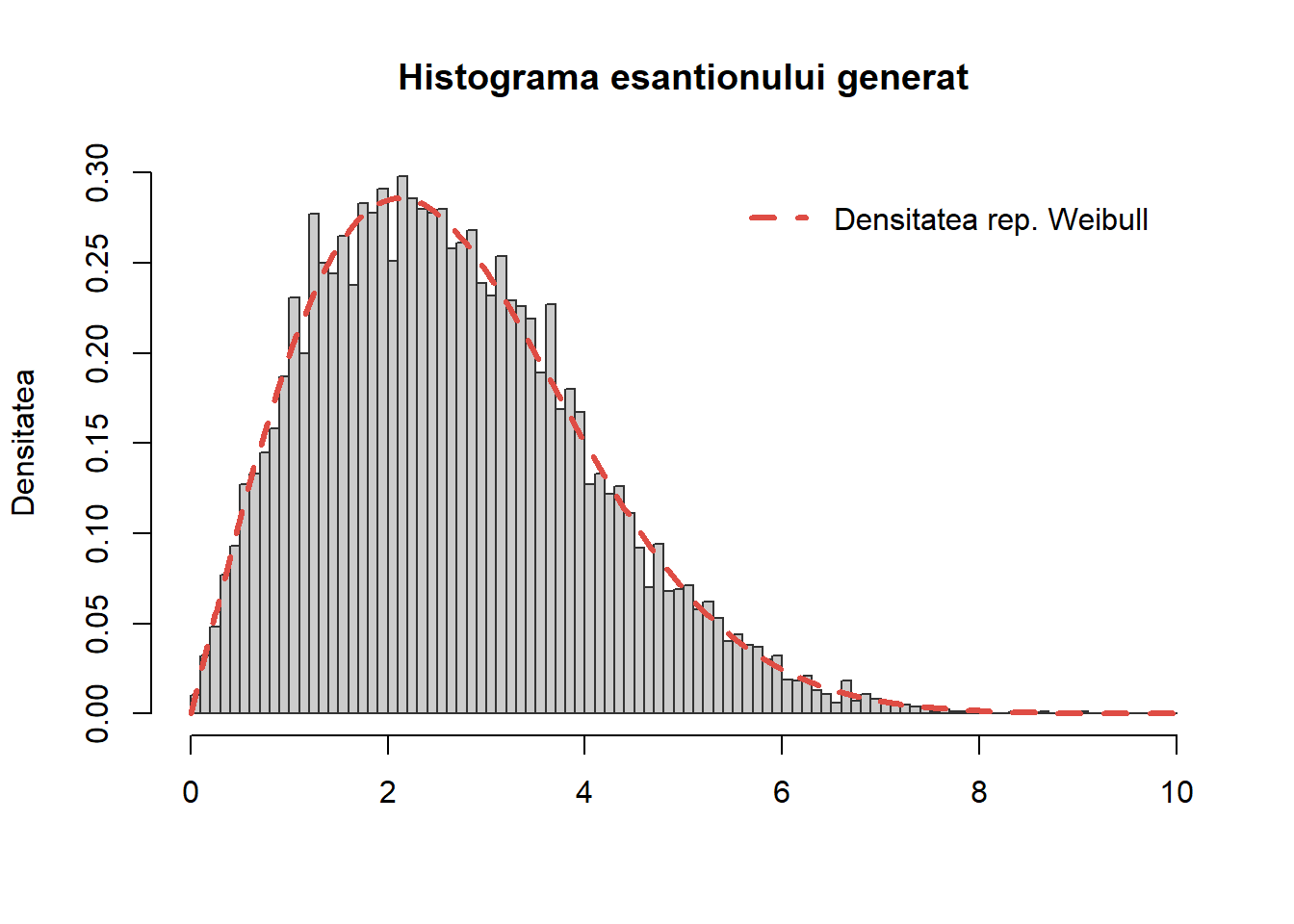
}Pentru a testa comparăm valorile simulate cu densitatea teoretică
Să observăm că pentru \(\alpha = 1\), densitatea de repartiție a repartiției Weibull coincide cu cea a repartiției Exponențiale. De asemenea, în R putem folosi funcția rweibull() pentru a genera observații din \(\mathrm{Weib}(\alpha, \beta)\).
Repartiția Cauchy
Exercițiul 9 Scrieți o funcție care să folosească metoda transformării inverse pentru a genera \(n\) observații dintr-o repartiție Cauchy de parametrii \(\alpha\) și \(\beta\) - \(\mathrm{C}(\alpha, \beta)\).
Soluție. Reamintim că variabila aleatoare \(X\) este repartizată Cauchy de parametrii \((\alpha, \beta)\), cu \(-\infty<\alpha<\infty\) și \(\beta>0\), și notăm \(X\sim \mathrm{C}(\alpha, \beta)\), dacă densitatea ei de repartiție este dată de
\[ f_X(x) = \frac{1}{\pi\beta} \frac{1}{1+\left(\frac{x-\alpha}{\beta}\right)^2},\quad \forall x\in\mathbb{R}. \]
Trebuie specificat că media și varianța variabilei aleatoare \(\mathrm{C}(\alpha, \beta)\) nu există. Funcția de repartiție este dată de
\[ F(x) = \int_{-\infty}^x \frac{1}{\beta \pi}\left(1+\frac{(t-\alpha)^2}{\beta^2}\right)^{-1} \mathrm{~d} t = \frac{1}{2}+\frac{1}{\pi} \arctan\left(\frac{x-\alpha}{\beta}\right) \]
iar funcția cuantilă devine
\[ F^{-1}(u) = \alpha+\beta \tan \left(\pi\left(u-\frac{1}{2}\right)\right). \]
Astfel din Teorema de uniersalitate, generând \(U\sim\mathcal{U}([0,1])\) avem că \(X\) definit de relația de mai sus este repartizat \(\mathrm{C}(\alpha, \beta)\). Următoarea funcție implementează acest procedeu:
sim_cont_cauchy <- function(n = 1, alpha = 0, beta = 1){
# n - nr de obs
# alpha - parametrul de locatie
# beta - parametrul de scala
u <- runif(n)
x <- alpha + beta*tan(pi*(u - 0.5))
return(x)
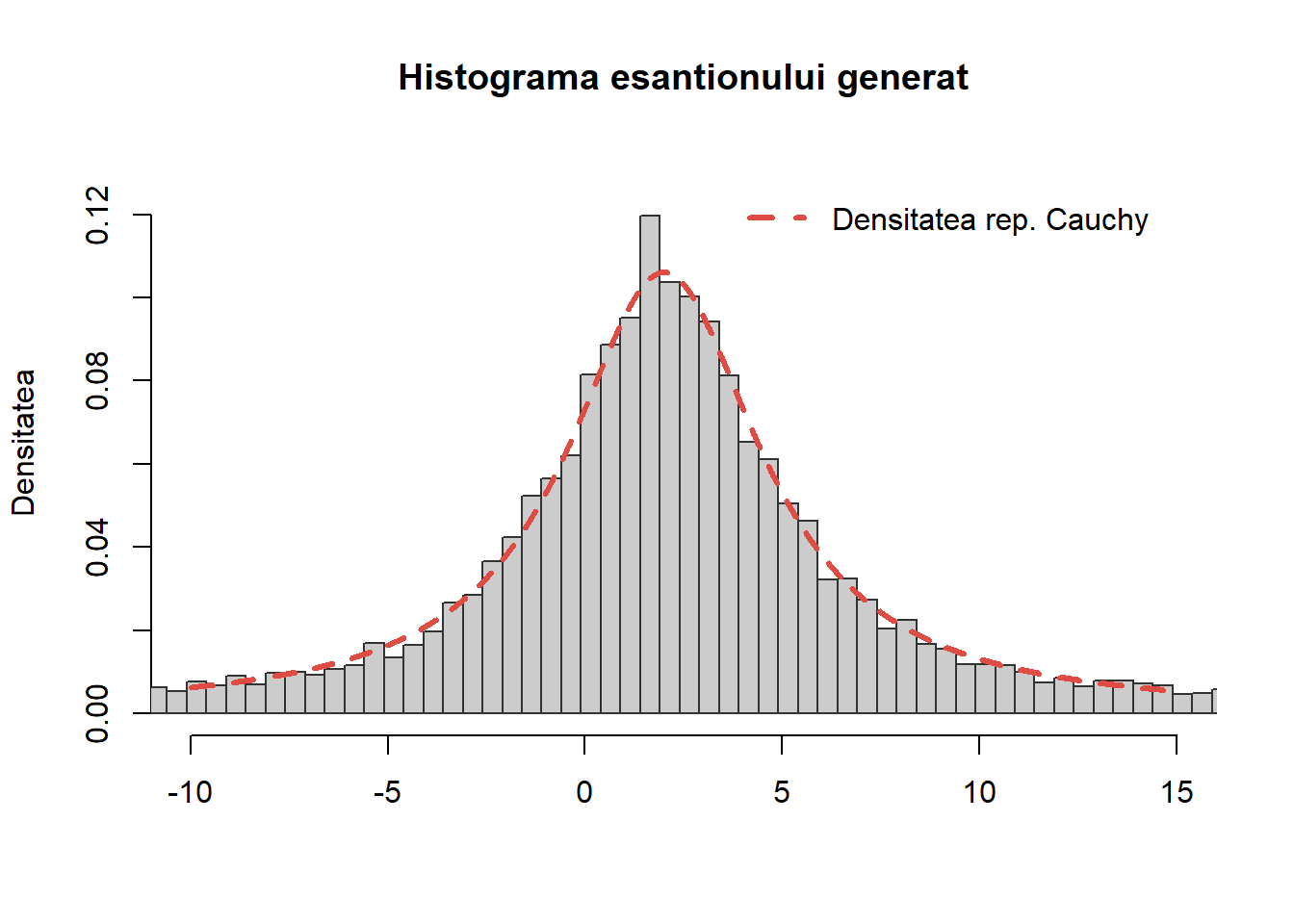
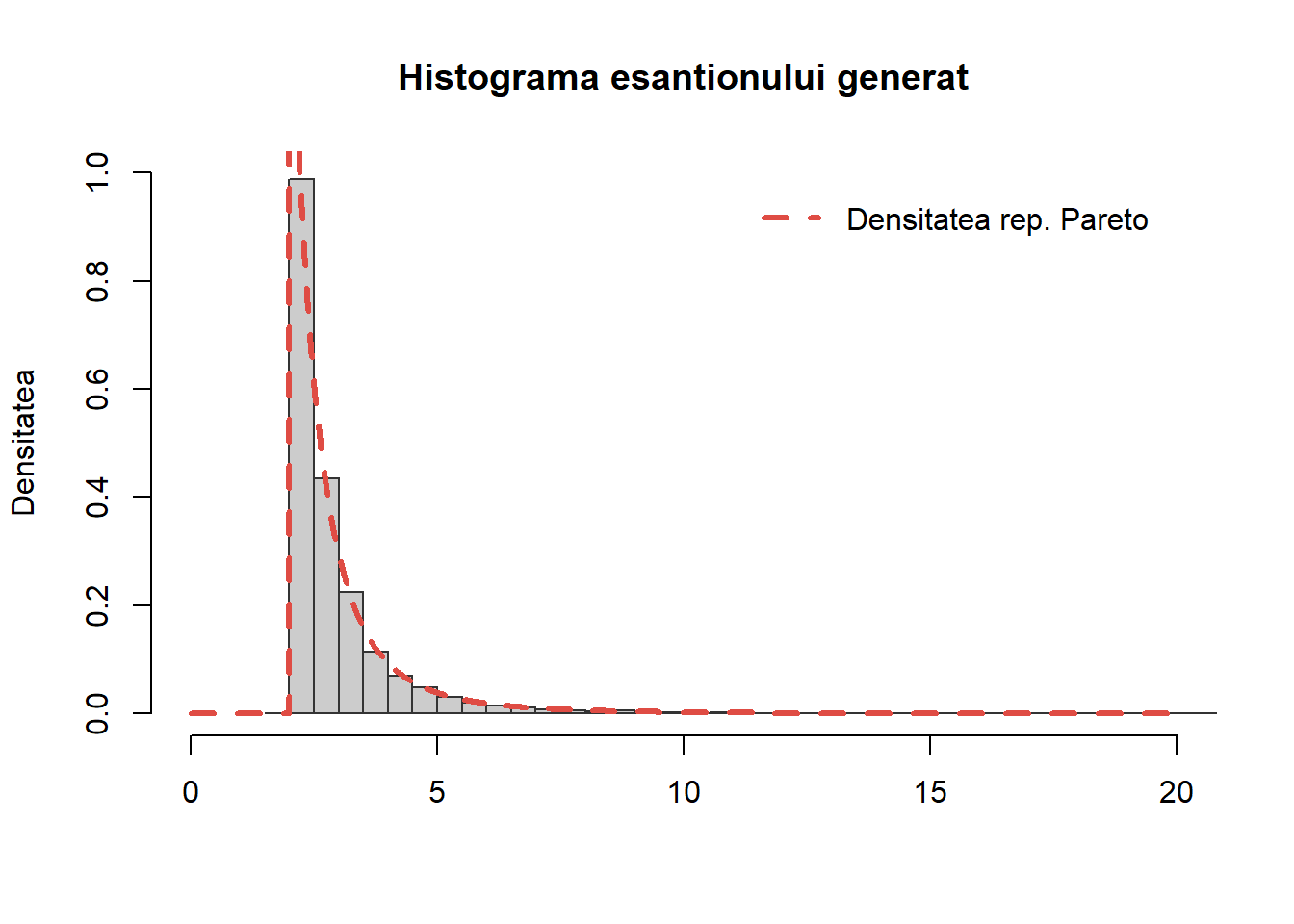
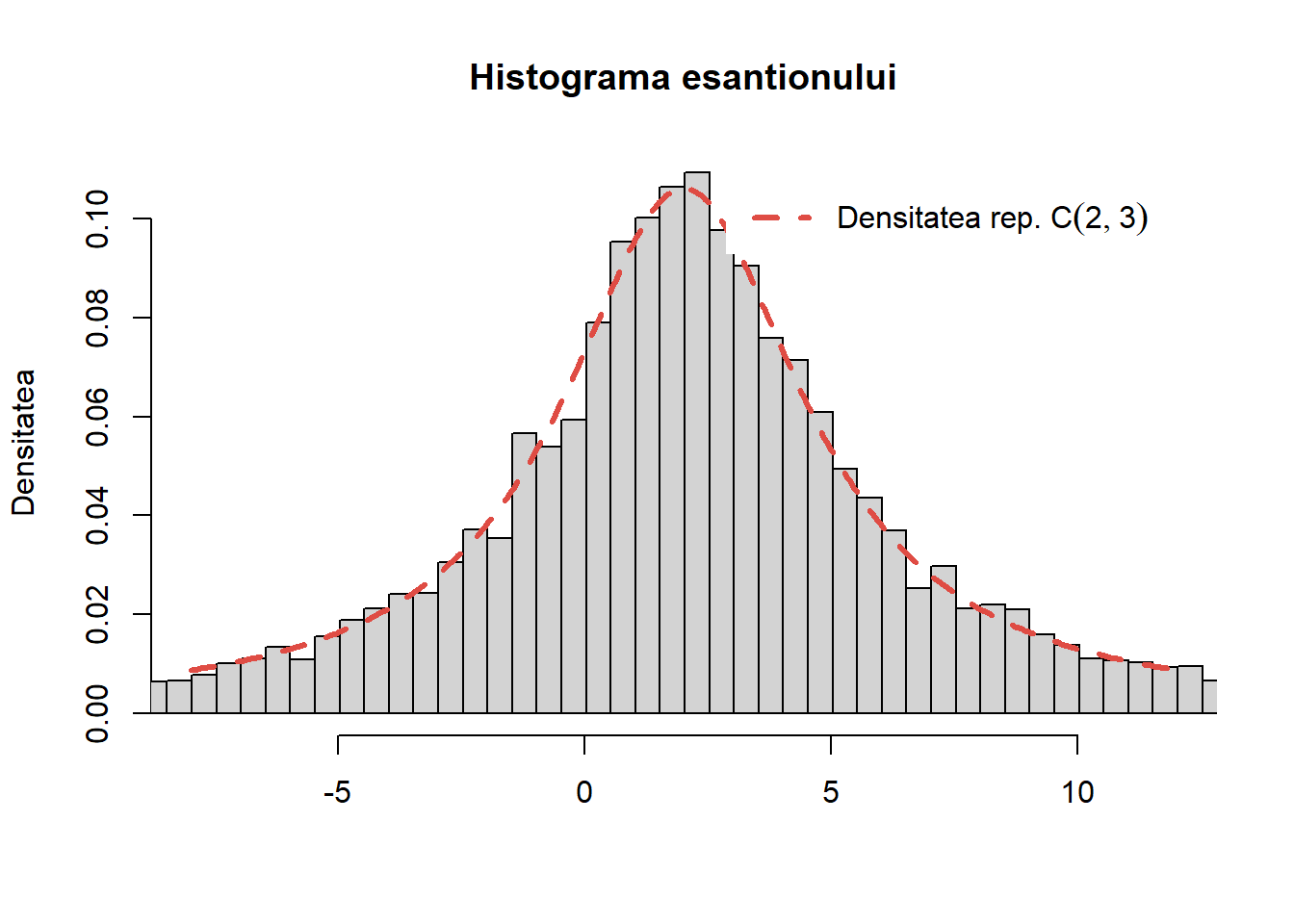
}Figura de mai jos compară histograma unui eșantion de volum \(10000\) de observații din \(\mathrm{C}(2, 3)\) cu repartiția teoretică:
În R putem folosi funcția rcauchy() pentru a simula observații din repartiția \(\mathrm{C}(\alpha, \beta)\). O altă modalitate de generare a observațiilor din repartiția Cauchy este dată în Exercițiul 25.
Repartiția Logistică
Exercițiul 10 Scrieți o funcție care să folosească metoda transformării inverse pentru a genera \(n\) observații dintr-o repartiție Logistică de parametrii \(\alpha\) și \(\beta\), \(\mathrm{Logis}(\alpha, \beta)\).
Soluție. Spunem că o variabilă aleatoare \(X\) este repartizată Logistic de parametrii \(-\infty<\alpha<\infty\) și \(\beta>0\), notat \(X\sim\mathrm{Logis}(\alpha, \beta)\), dacă admite ca densitate de repartiție pe
\[ f(x) = \frac{\exp \left(\frac{x-\alpha}{\beta}\right)}{\beta\left(1+\exp \left(\frac{x-\alpha}{\beta}\right)\right)^2}\mathbf{1}_{\mathbb{R}}(x). \]
Funcția de repartiție este dată de
\[ F(x) = \int_{-\infty}^x \frac{\exp \left(\frac{x-\alpha}{\beta}\right)}{\beta\left(1+\exp \left(\frac{x-\alpha}{\beta}\right)\right)^2} \mathrm{~d} t = \frac{1}{1+e^{-(x-\alpha) / \beta}} \]
iar un calcul direct conduce la funcția cuantilă
\[ F^{-1}(u) = \alpha+\beta \log \left(\frac{u}{1-u}\right). \]
Astfel pentru a genera \(X\sim\mathrm{Logis}(\alpha, \beta)\), considerăm \(U\sim\mathcal{U}([0,1])\) și luăm
\[ X = \alpha+\beta \log \left(\frac{U}{1-U}\right). \]
Următoarea funcție implementează această procedură:
sim_cont_logis <- function(n = 1, alpha = 0, beta = 1){
# n - nr de obs
# alpha - parametrul de locatie
# beta - parametrul de scala
u <- runif(n)
x <- alpha + beta*log(u/(1-u))
return(x)
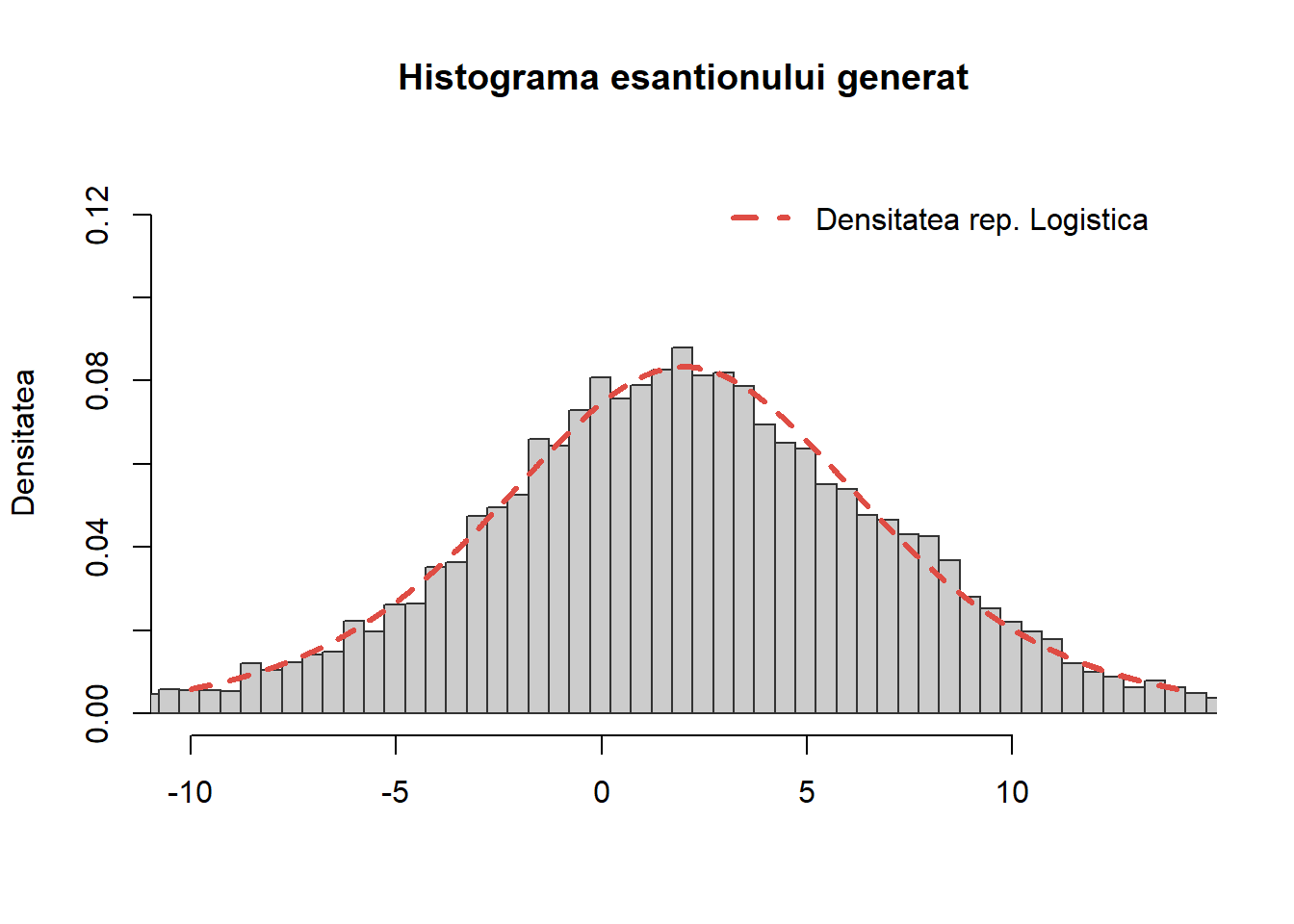
}Pentru a testa funcția, comparăm valorile simulate pentru un eșantion de volum \(n=10000\) de observații cu densitatea teoretică
În R putem folosi funcția rlogis() pentru a genera observații din \(\mathrm{Logis}(\alpha, \beta)\).
Repartiția Pareto
Exercițiul 11 Scrieți o funcție care să folosească metoda transformării inverse pentru a genera \(n\) observații dintr-o repartiție Pareto de parametrii \(\alpha\) și \(\beta\), \(\mathrm{Pareto}(\alpha, \beta)\).
Soluție. Spunem că o variabilă aleatoare \(X\) este repartizată Pareto de parametrii \(\alpha>0\) și \(\beta>0\), notat \(X\sim\mathrm{Pareto}(\alpha, \beta)\), dacă admite ca densitate de repartiție pe
\[ f(x) = \begin{cases}\beta \alpha^\beta x^{-\beta-1}, & \text { pentru } \alpha<x<\infty, \\ 0, & \text { altfel}\end{cases}. \]
Integrând densitatea, obținem că funcția de repartiție este dată de
\[ F(x)=\int_\alpha^x \beta \alpha^\beta t^{-\beta-1} \mathrm{~d} t=1-\left(\frac{\alpha}{x}\right)^\beta \]
ceea ce conduce la funcția cuantilă
\[ F^{-1}(u) = \alpha(1-u)^{-1 / \beta}. \]
Astfel pentru a genera \(X\sim\mathrm{Pareto}(\alpha, \beta)\), luăm \(U\sim\mathcal{U}([0,1])\) și, ținând cont că \(1-U\sim\mathcal{U}([0,1])\), rezultă
\[ X = \alpha(1-U)^{-1 / \beta}\sim\mathrm{Pareto}(\alpha, \beta). \]
Următoarea funcție implementează această procedură:
sim_cont_pareto <- function(n = 1, alpha = 0, beta = 1){
# n - nr de obs
# alpha - parametrul de forma
# beta - parametrul de scala
u <- runif(n)
x <- alpha*(u)^(-1/beta)
return(x)
}Pentru a testa funcția, comparăm valorile simulate pentru un eșantion de volum \(n=10000\) de observații cu densitatea teoretică
În R nu avem funcții predefinite aferente repartiției Pareto (rpareto, dpareto, ppareto sau qpareto) dar, ca și în cazul repartiției Laplace, acestea pot fi construite pe baza formulelor de mai sus.
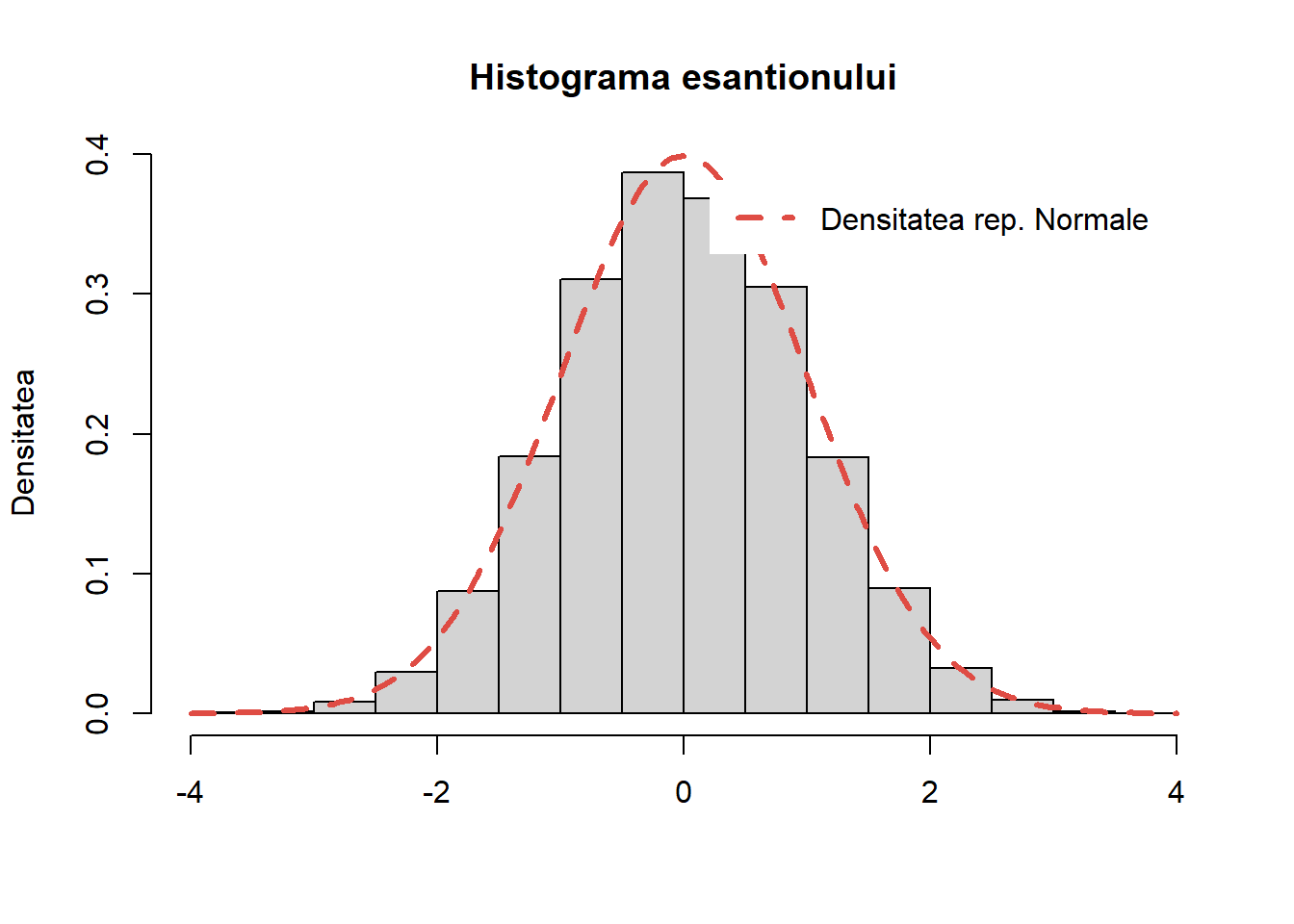
Repartiția Normală
Exercițiul 12 Scrieți o funcție care să folosească metoda transformării inverse pentru a genera \(n\) observații dintr-o repartiție Normală de parametrii \(\mu\) și \(\sigma^2\), \(\mathcal{N}(\mu, \sigma^2)\).
Vom prezenta mai jos, în ?@sec-gen-inv-other-norm, o metodă de generare a observațiilor dintr-o repartiție \(\mathcal{N}(0, 1)\) folosindu-ne de transformarea Box-Muller, unde plecând de la două observații uniforme independente se obțin două observații repartizate normal și independente. De asemenea, în Exercițiul 16, vom ilustra o altă metodă de generare a unei normale folosind metoda respingerii.
Soluție. În acest exemplu vom considera o metodă de generare bazată pe metoda inversă. Cu toate că în cazul repartiției normale nu avem o formă compactă a funcției de repartiție \(\Phi(x)\) sau a funcției cuantilă \(\Phi^{-1}(u)\) și prin urmare nu putem aplica în mod direct această metodă, în literatură au fost propuși mai mulți algoritmi de aproximare a lui \(\Phi^{-1}(u)\) (a se vedea de exemplu (Odeh, Evans, et al. 1974) sau (Wichura 1988)). Conform (Odeh, Evans, et al. 1974), dacă \(X\sim\mathcal{N}(0,1)\) atunci pentru \(10^{-20}<u<1-10^{-20}\) putem aproxima funcția cuantilă prin
\[ \Phi^{-1}(u) = y + \frac{S_4(y)}{T_4(y)} = y + \frac{a_0 + a_1 y + a_2 y^2 + a_3 y^3 + a_4 y^4}{b_0 + b_1 y + b_2 y^2 + b_3 y^3 + b_4 y^4} \]
unde \(y = \sqrt{-2\log(u)}\) iar \(S_4(y)\) și \(T_4(y)\) sunt polinoame de gradul \(4\). Conform autorilor, eroarea maximă de aproximare este de ordinul \(1.5\times 10^{-8}\). Următorul cod implementează această aproximare:
q_norm_OE <- function(p, mean = 0, sd = 1){
# functia cuantila dupa Odeh 1974
# coeficientii polinoamelor S_4 si T_4
a0 <- -0.322232431088
a1 <- -1.0
a2 <- -0.342242088547
a3 <- -0.204231210245e-1
a4 <- -0.453642210148e-4
b0 <- 0.993484626060e-1
b1 <- 0.588581570495
b2 <- 0.531103462366
b3 <- 0.103537752850
b4 <- 0.385607006340e-2
ps <- p
ps <- ifelse(ps > 0.5, 1-ps, ps)
y <- sqrt(-2*log(ps))
out <- y + ((((y*a4+a3)*y+a2)*y+a1)*y+a0) /
((((y*b4+b3)*y+b2)*y+b1)*y+b0)
out <- ifelse(ps == 0.5, 0, out)
out <- ifelse(p < 0.5, - out, out)
out <- mean + sd*out
return(out)
}Vom testa această funcție comparând cu rezultatul obținut prin aplicarea funcției qnorm() (care implementează algoritmul din (Wichura 1988)):
| t | qnorm | qnorm_OE | error |
|---|---|---|---|
| 0.05 | -1.6448536 | -1.6448536 | 0 |
| 0.10 | -1.2815516 | -1.2815516 | 0 |
| 0.15 | -1.0364334 | -1.0364334 | 0 |
| 0.20 | -0.8416212 | -0.8416212 | 0 |
| 0.25 | -0.6744898 | -0.6744897 | 0 |
| 0.30 | -0.5244005 | -0.5244005 | 0 |
| 0.35 | -0.3853205 | -0.3853205 | 0 |
| 0.40 | -0.2533471 | -0.2533471 | 0 |
| 0.45 | -0.1256613 | -0.1256613 | 0 |
| 0.50 | 0.0000000 | 0.0000000 | 0 |
| 0.55 | 0.1256613 | 0.1256613 | 0 |
| 0.60 | 0.2533471 | 0.2533471 | 0 |
| 0.65 | 0.3853205 | 0.3853205 | 0 |
| 0.70 | 0.5244005 | 0.5244005 | 0 |
| 0.75 | 0.6744898 | 0.6744897 | 0 |
| 0.80 | 0.8416212 | 0.8416212 | 0 |
| 0.85 | 1.0364334 | 1.0364334 | 0 |
| 0.90 | 1.2815516 | 1.2815516 | 0 |
| 0.95 | 1.6448536 | 1.6448536 | 0 |
Aplicând metoda inversă obținem următoarea funcție pentru generarea unei observații normale:
sim_cont_normal <- function(n, mean = 0, sd = 1){
u <- runif(n)
x <- q_norm_OE(u, mean = mean, sd = sd)
return(x)
}Verificăm algoritmul prin trasarea histogramei:
Generarea variabilelor aleatoare prin metoda respingerii
În această secțiune vom prezenta o serie de exerciții aplicative ale metodei de simulare bazate pe acceptare-respingere. Astfel, vom începe prin descrierea modului în care putem genera observații repartizate uniform pe o mulțime din \(\mathbb{R}^d\) în Secțiunea 0.4.1, continuând apoi cu descrierea principiului metodei de acceptare-respingere pentru cazul variabilelor aleatoare care admit densitate în Secțiunea 0.4.2 și încheind cu aplicarea metodei pentru cazul discret în Secțiunea 0.4.3.
Generarea variabilelor aleatoare repartizate uniform pe o mulțime dată
Vom începe această secțiune prin a ne reaminti definiția repartiției uniforme pe o mulțime boreliană dată:
Definiția 1 (Repartiția Uniformă pe o mulțime) Fie \((\Omega, \mathcal{F}, \mathbb{P})\) un câmp de probabilitate și \(B\in\mathcal{B}_{\mathbb{R}^d}\) o mulțime boreliană astfel încât \(0< \lambda_d(B)<\infty\) (\(\lambda_d\) este măsura Lebesgue pe \(\mathbb{R}^d\)). Spunem că vectorul aleator \(M:\Omega\to\mathbb{R}^d\) este repartizat uniform pe \(B\), și notăm \(M\sim \mathcal{U}(B)\), dacă repartiția sa verifică
\[ \left(\mathbb{P}\circ M^{-1}\right)(A) = \mathbb{P}(M\in A) = \frac{\lambda_d(A\cap B)}{\lambda_d(B)}, \quad \forall\, A\in\mathcal{B}_{\mathbb{R}^d}. \]
Următorul rezultat stă la baza metodei de generare a observațiilor repartizate uniform pe o mulțime boreliană dată:
Propoziția 1 (Generarea prin metoda respingerii dintr-o repartiție condiționată) Fie \((\Omega, \mathcal{F}, \mathbb{P})\) un câmp de probabilitate și \((M_n)_n\) un șir de vectori aleatori, \(M:\Omega\to\mathbb{R}^d\), independenți și de repartiție comună \(\mu\). Fie \(B\in\mathcal{B}_{\mathbb{R}^d}\) o mulțime boreliană astfel încât \(\mu(B)>0\). Pentru toți \(\omega\in\Omega\) luăm
\[ T(\omega) = \inf\{n\in\mathbb{N}^{*}\,|\,M_n(\omega)\in B\} \] adoptând convenția \(\inf\emptyset = \infty\). Definim \(M_{T}:\Omega\to\mathbb{R}^d\) prin
\[ M_{T}(\omega)=\left\{\begin{array}{ll} M_{T(\omega)}(\omega), & T(\omega)<\infty\\ 0, & T(\omega) = \infty \end{array}\right. \]
Atunci
\(\mathbb{P}(T<\infty)=1\) și dacă \(T'=T\mathbf{1}_{T<\infty}\) atunci \(T'\sim\mathrm{Geom}(\mu(B))\)
\(M_{T}\) este un vector aleator de repartiție \(\nu\) definită prin
\[ \nu(A) = \mathbb{P}(M_{T}\in A) = \frac{\mu(A\cap B)}{\mu(B)}, \quad \forall\, A\in\mathcal{B}_{\mathbb{R}^d}. \]
Cu alte cuvinte \(\nu\) este repartiția condiționată \(\mu(\cdot|B)\).
Demonstrație. Pentru a), vom începe prin a justifica măsurabilitatea lui \(T\) și \(T'\). Observăm că \(T:\Omega\to\overline{\mathbb{N}^{*}}\) unde \(\overline{\mathbb{N}^{*}}=\mathbb{N}^{*} \cup\{+\infty\}\) iar \(T':\Omega\to\mathbb{N}^{*}\), prin urmare măsurabilitatea implică \(\mathcal{F}\) și \(\mathcal{P}\left(\overline{\mathbb{N}^{*}}\right)\). Ținând cont de numărabilitatea lui \(\overline{\mathbb{N}^{*}}\), este suficient să verificăm
\[ \forall k \in \overline{\mathbb{N}^{*}}, \quad T^{-1}(\{k\}) \in \mathcal{F} \quad (\forall k \in \mathbb{N}^{*}, \quad T'^{-1}(\{k\}) \in \mathcal{F}). \]
Pentru \(k \in \mathbb{N}^{*}\), obținem \(T^{-1}(\{k\})=T'^{-1}(\{k\})\) cu
\[ \begin{aligned} T^{-1}(\{k\}) & =\{w \mid T(w)=k\} \\ & =\left\{w \mid M_i(w) \notin B, i<k, M_k(w) \in B\right\} \\ & =\bigcap_{1 \leq i<k}\left\{M_i \notin B\right\} \cap\left\{M_k \in B\right\} \\ & =\bigcap_{1 \leq i<k}\left\{M_i \in B^c\right\} \cap\left\{M_k \in B\right\} \\ & =\bigcap_{i<k} \underbrace{M_i^{-1}\left(B^c\right)}_{\in F} \cap \underbrace{M_k^{-1}(B)}_{\in F} \in \mathcal{F} \end{aligned} \]
unde, ținând seama de măsurabilitatea vectorilor \(M_i\) de la \(\mathcal{F}\) la \(\mathcal{B}_{\mathbb{R}^d}\), avem că \(M_i^{-1}(B^c)\in\mathcal{F}\). În mod similar, pentru \(k=+\infty\) avem \(\{T'=0\} = \{T=+\infty\}\) iar
\[ \begin{aligned} \{T=+\infty\} & =\left\{w \mid \forall n \geqslant 1, M_n(w) \notin B\right\} \\ & =\bigcap_{n \geqslant 1}\left\{M_n \notin B\right\}=\bigcap_{n \geqslant 1} \underbrace{M_n^{-1}\left(B^c\right)}_{\in \mathcal{F}} \in \mathcal{F} \end{aligned} \]
de unde concluzionăm că \(T\) și respectiv \(T'\) sunt funcții măsurabile.
Pentru a determina repartiția lui \(T\), respectiv a lui \(T'\), să observăm că pentru \(k \in \mathbb{N}^{*}\),
\[ \begin{aligned} \mathbb{P}(T'=k) &= \mathbb{P}(T=k) =\mathbb{P}\left(\bigcap_{i<k} M_i^{-1}\left(B^c\right) \cap M_k^{+1}(B)\right) \\ & \overset{indep.}{=}\prod_{1 \leqslant i<k} \mathbb{P}\left(M_i^{-1}\left(B^c\right)\right) \times \mathbb{P}\left(M_k^{-1}(B)\right) \\ & = \prod_{1 \leqslant i<k}\left(1-\underbrace{\mathbb{P} \circ M_i^{-1}}_{\mu}(B)\right) \times \underbrace{\left(\mathbb{P} \circ M_k^{-1}\right)}_{\mu}(B) \\ & = \prod_{1 \leq i<k}(1-\mu(B)) \times \mu(B)=(1-\mu(B))^{k-1} \mu(B) \end{aligned} \]
iar pentru \(k=+\infty\)
\[ \begin{aligned} \mathbb{P}(T'=0) = \mathbb{P}(T=+\infty) =\mathbb{P}\left(\bigcap_{n \geqslant 1} M_n^{-1}\left(B^c\right)\right). \end{aligned} \]
Din ipoteză avem că \(\mu(B)>0\), prin urmare \(1-\mu(B)<1\) și ținând cont că
\[ \bigcap_{n \geqslant 1} M_n^{-1}\left(B^c\right) \subseteq \bigcap_{i=1}^m M_i^{-1}\left(B^c\right), \quad \forall m \geqslant 1 \]
aplicând monotonia măsurii de probabilitate avem
\[ \begin{aligned} \mathbb{P}(T'=0) &= \mathbb{P}\left(T=+\infty\right) = \mathbb{P}\left(\bigcap_{n \geqslant 1} M_n^{-1}\left(B^c\right)\right) \leq \mathbb{P}\left(\bigcap_{i=1}^m M_i^{-1}\left(B^c\right)\right)\\ & \overset{indep.}{=} \prod_{1 \leqslant i\leqslant m} \mathbb{P}\left(M_i^{-1}\left(B^c\right)\right) = \prod_{i=1}^m(1-\mu(B))=(1-\mu(B))^m, \quad \forall m \geqslant 1 \end{aligned} \]
de unde pentru \(m\to\infty\) rezultă \(\mathbb{P}(T'=0)=\mathbb{P}\left(T=+\infty\right)=0\). Astfel, \(T'\sim\mathrm{Geom}(\mu(B))\).
- Vom arăta pentru început că \(M_{T}\) este un vector aleator, adică o aplicație măsurabilă de la \(\mathcal{F}\) la \(\mathcal{B}_{\mathbb{R}^{d}}\), demonstrând că \(M_{T}^{-1}(A) \in \mathcal{F}\) pentru orice \(A \in \mathcal{B}_{\mathbb{R}^{d}}\). Partiționând \(\Omega\) după evenimentele \(\{T=k\}\), avem următoarea descompunere
\[ \begin{aligned} M_T^{-1}(A) & =M_T^{-1}(A) \cap \Omega = M_T^{-1}(A) \cap \bigcup_{k \in \overline{\mathbb{N}^{*}}}\{T = k\}\\ & =\bigcup_{k \in \overline{\mathbb{N}^{*}}}\left(M_T^{-1}(A) \cap T^{-1}(\{k\})\right) \end{aligned} \]
Cum această reuniune este numărabilă este suficient să verificăm că fiecare element aparține lui \(\mathcal{F}\). Dacă \(k \in \mathbb{N}^{*}\), atunci
\[ \begin{aligned} M_T^{-1}(A) \cap T^{-1}(\{k\}) & =\left\{\omega \mid M_T(\omega) \in A, T(\omega)=k\right\} \\ & =\left\{\omega \mid M_k(\omega) \in A, T(\omega)=k\right\} \\ & =\bigcap_{i<k}\left\{M_i \notin B\right\} \cap\left\{M_k \in B\right\} \cap\left\{M_k \in A\right\} \\ & =\bigcap_{i<k} \left\{M_i \notin B\right\} \cap\{M_k \in A \cap B\} \\ & = \bigcap_{i<k} \underbrace{M_{i}^{-1}\left(B^{c}\right)}_{\in \mathcal{F}} \cap \underbrace{M_{k}^{-1}(A \cap B)}_{\in \mathcal{F}} \in \mathcal{F} \end{aligned} \]
În cazul \(k=+\infty\),
\[ \left\{M_{T} \in A\right\} \cap\{T=+\infty\}=\bigcap_{i \in \mathbb{N}^{*}} M_{i}^{-1}\left(B^{c}\right) \cap\left\{M_{\infty} \in A\right\} \]
dar \(M_{\infty}\) este vectorul aleator constant \(0\), prin urmare \(\left\{M_{\infty} \in A\right\}\) este egal cu \(\Omega\) sau \(\emptyset\) după cum \(0\) aparține sau nu mulțimii \(A\). Avem astfel o intersecție numărabilă de elemente din \(\mathcal{F}\) și concluzionăm că \(M_{T}\) este un vector aleator.
Având măsurabilitatea lui \(M_{T}\) asigurată, putem să determinăm repartiția acestui vector aleator \(\nu\) pe care o determinăm calculând \(\nu(A)=\mathbf{P}\left(M_{T} \in A\right)\) pentru \(A \in \mathcal{B}_{\mathbb{R}^{d}}\). Partiționând \(\Omega\) după \(\{T=k\}\), ca mai sus, obținem:
\[ \begin{aligned} \nu(A) & =\mathbb{P}\left(M_T \in A\right)=\mathbb{P}\left(\bigcup_{k \in \overline{\mathbb{N}^{*}}}\left\{M_T \in A, T=k\right\}\right) \\ & \overset{\mathbb{P}(T=\infty)=0}{=}\sum_{k \in \mathbb{N}^{*}} \mathbb{P}\left(M_T \in A, T=k\right) \\ & \overset{indep.}{=} \sum_{k \in \mathbb{N}^{*}} \prod_{i<k} \mathbb{P}\left(M_i \notin B\right) \times \mathbb{P}\left(M_k \in A \cap B\right) \\ & =\sum_{k \in \mathbb{N}^{*}} \prod_{i<k}(1-\mu(B)) \times\mu(A \cap B)=\sum_{k \geqslant 1}(1 - \mu(B))^{k-1} \mu(A\cap B)\\ & = \mu(A \cap B) \frac{1}{1-(1-\mu(B))}=\frac{\mu(A \cap B)}{\mu(B)} \end{aligned} \]
ceea ce arată că \(\nu\) este repartiția condiționată \(\mu(\cdot|B)\).
Ca aplicație a rezultatului de mai sus considerăm următorul exercițiu:
Exercițiul 13 (Uniforma pe disc) Considerăm pătratul \(C = [0,L]^2\) și discul \(D\) de centru \((\frac{L}{2},\frac{L}{2})\) și rază \(\frac{L}{2}\). Considerăm șirul de v.a. \(\left(Y_n\right)_{n\geq1}\) pe \(\mathbb{R}^2\) i.i.d. repartizate uniform pe pătratul \(C\).
- Aproximați valoarea lui \(\pi\) prin ajutorul numărului de puncte \(Y_n\) care cad în interiorul discului \(D\) (Metoda respingerii)
- Simulați \(n\) puncte uniforme pe disc.
Soluție. Pentru primul punct avem:
- Definim v.a. \(X_n=\mathbf{1}_{\{Y_n\in D\}}\), \(n\geq1\), care formează un șir de v.a. i.i.d. de repartiție \(\mathcal{B}(\mathbb{P}(Y_n\in D))\), deoarece \(\left(Y_n\right)_{n\geq1}\) este un șir de v.a. i.i.d. repartizate uniform pe \(C\), \(\mathcal{U}(C)\). Din Legea Numerelor Mari avem că
\[ \displaystyle\frac{1}{n}\sum_{i=1}^{n}X_{i} \overset{a.s.}{\to} \mathbb{E}[X_1] = \mathbb{P}(Y_1\in D), \]
prin urmare trebuie să calculăm probabilitatea \(\mathbb{P}(Y_1\in D)\). Știm că densitatea v.a. \(Y_1\) este dată de \(f_{Y_1}(x,y)=\frac{1}{\mathcal{A}(C)}\mathbf{1}_{C}(x,y)\) de unde
\[ \begin{aligned} \mathbb{P}(Y_1\in D) &= \iint_{D}f_{Y_1}(x,y)\,dxdy = \iint \mathbf{1}_{D}(x,y)\mathbf{1}_{C}(x,y)\,dxdy\\ &= \frac{1}{\mathcal{A}(C)}\iint \mathbf{1}_{D}(x,y)\,dxdy = \frac{\mathcal{A}(D)}{\mathcal{A}(C)} = \frac{\pi \frac{L^2}{4}}{L^2} = \frac{\pi}{4}. \end{aligned} \]
Astfel, putem estima valoarea lui \(\pi\) prin \(\displaystyle\frac{4}{n}\sum_{i=1}^{n}X_{i}\) pentru valori mari ale lui \(n\).
# Estimam valoarea lui pi
L <- 3 # lungimea laturii patratului
R <- L/2 # raza cercului inscris
n <- 2000 # numarul de puncte din patratul C
# generam puncte uniforme in C
x <- L*runif(n)
y <- L*runif(n)
# metoda respingerii
l <- (x-R)^2+(y-R)^2 # distanta dintre centrul cercului si punct
ind <- l<=(R)^2 # indicii pentru care distanta este mai mica sau egala cu R
xc <- x[ind] # coordonatele punctelor din interiorul cercului
yc <- y[ind]
estimate_pi <- 4*sum(ind)/n # estimarea lui pi
err <- abs(estimate_pi-pi) # eroarea absolutaAplicând acest procedeu obținem că valoarea estimată a lui \(\pi\) prin generarea a \(n=\) 2000 puncte este 3.138 iar eroarea absoluta este 0.003593.
Pentru punctul doi:
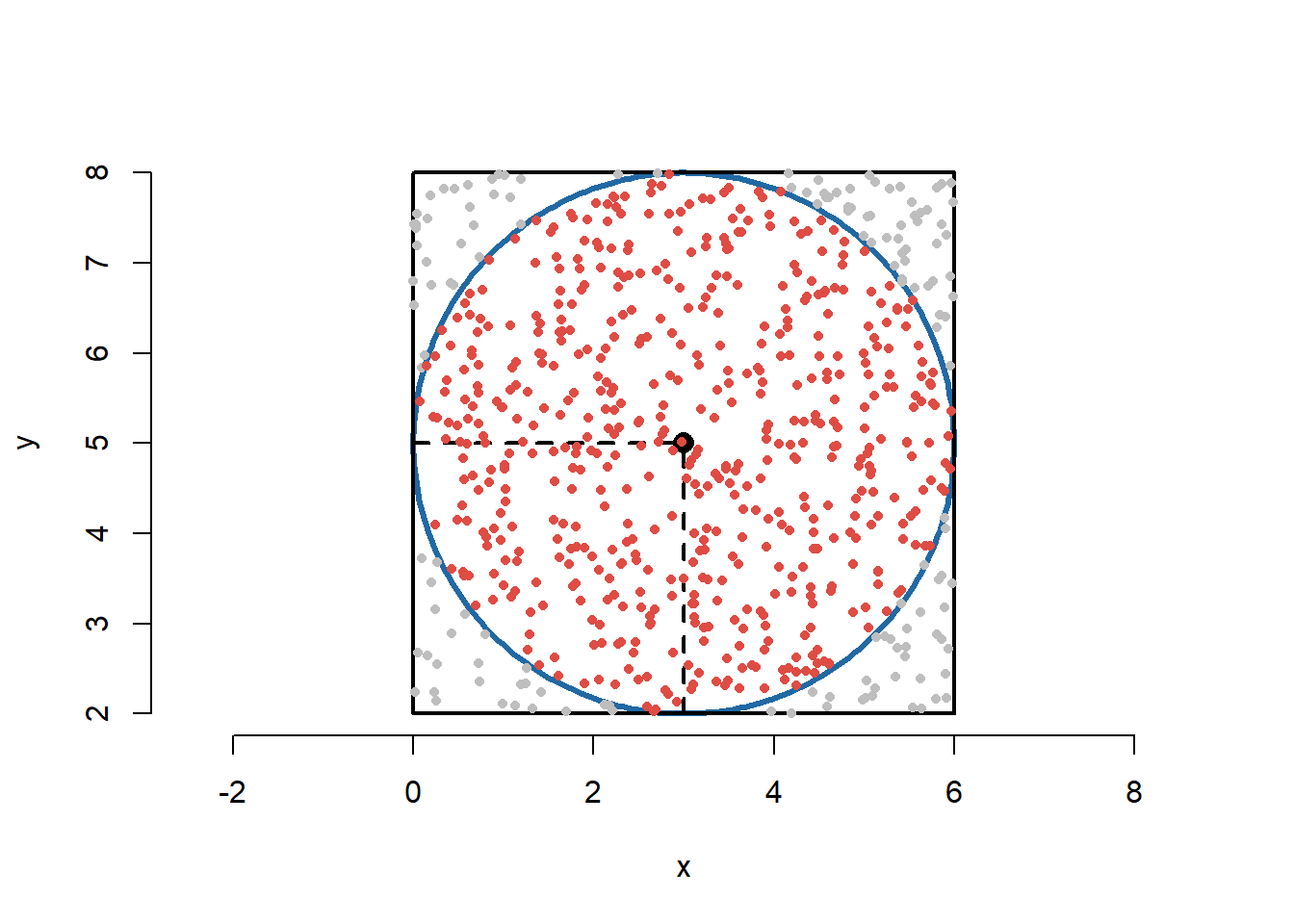
- Una dintre metodele prin care putem simula puncte repartizate uniform pe suprafața discului \(D\) este Metoda respingerii așa cum este descrisă la începutul secțiunii. Această metodă consistă în generarea de v.a. \(Y_n\) repartizate uniform pe suprafața pătratului \(C\), urmând ca apoi să testăm dacă \(Y_n\) aparține discului \(D\) (deoarece \(D\subset C\)). Dacă da, atunci le păstrăm, dacă nu, atunci mai generăm. Următoarea figură ilustrează această metodă:
Funcția de mai jos permite generarea a \(n\) observații repartizate uniform pe discul \(D\) de centru \((xc, yc)\) și rază \(R\):
gen_unif_disc <- function(n = 10, R = 2, xc = 2, yc = 2){
# n - nr observatii
# R - raza cercului
# xc, yc - centrul cercului
# j (output) - nr de obs necesar pentru generarea unei obs
out <- matrix(0, ncol = 3, nrow = n)
for (i in 1:n){
d <- R^2 + 1
j <- 0
while(d > R^2){
x <- xc - R + 2*R*runif(1)
y <- yc - R + 2*R*runif(1)
d <- (x - xc)^2 + (y - yc)^2
j <- j + 1
}
out[i, ] <- c(x, y, j)
}
return(out)
}Putem observa că numărul mediu de puncte repartizate uniform pe \(C\) necesare pentru a genera un punct uniform pe \(D\) este \(4/\pi\) (raportul dintre aria pătratului și aria discului). Acest fenomen se poate observa și prin simulare. Atunci când generăm \(n=1000\) de puncte repartizate uniform pe discul \(D\) de centru \((xc,yc)=(\frac{L}{2},\frac{L}{2})=(1.5,1.5)\) și rază \(R=\frac{L}{2} = 1.5\), obținem un număr mediu de puncte de 1.278, cu o eroare de 0.0047605.
Metodă alternativă: Vom prezenta mai jos o altă metodă de simulare a punctelor distribuite uniform pe discul \(D\) de rază \(L\).
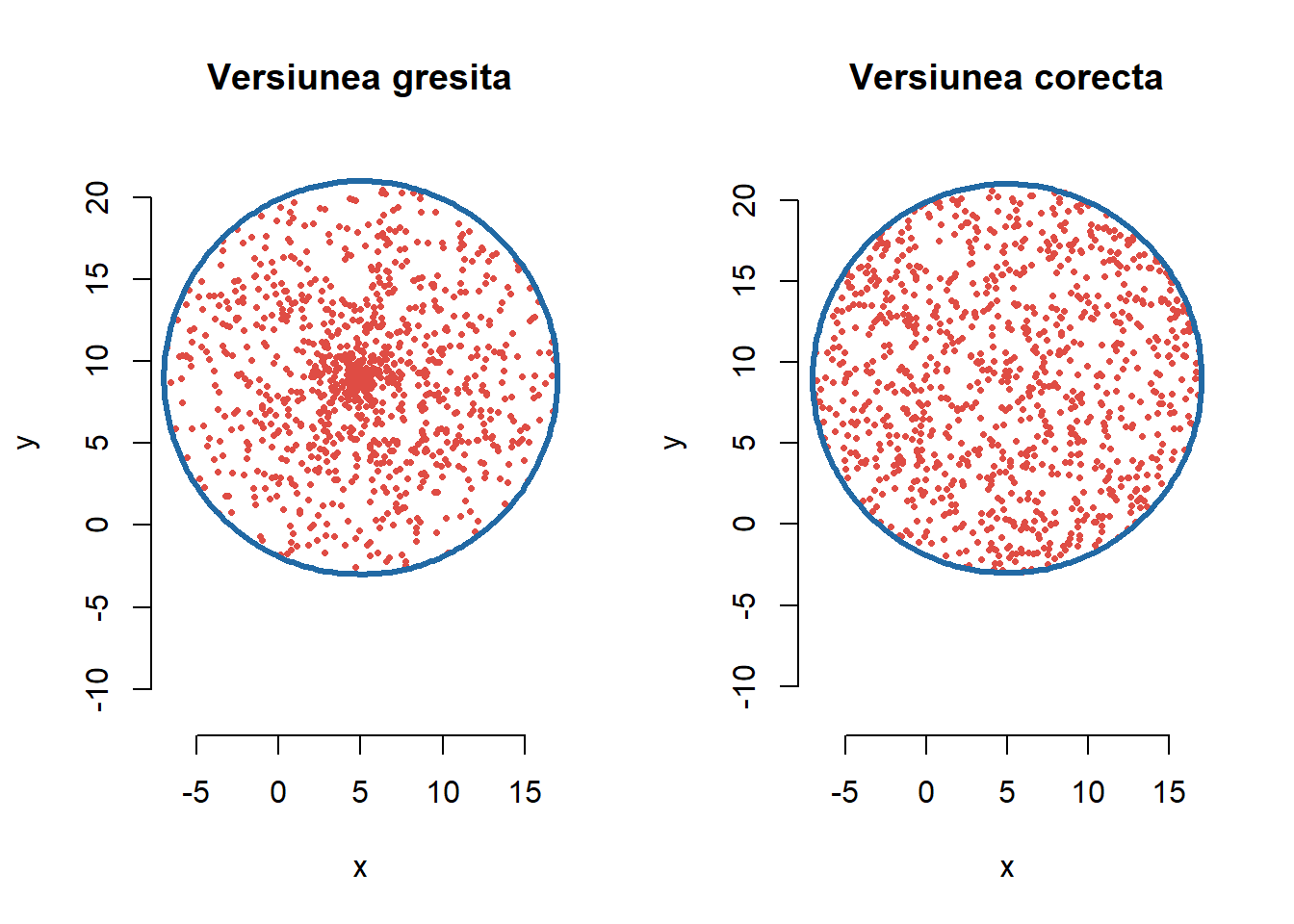
O primă idee, eronată, ar fi să generăm cuplul de v.a. \((X_1,Y_1)\) astfel încât, ținând seama de schimbarea de variabile în coordonate polare, \(X_1 = \tilde{R}\cos(\tilde{\Theta})\) și \(Y_1 = \tilde{R}\sin(\tilde{\Theta})\) unde \(\tilde{R}\sim\mathcal{U}([0,L])\), \(\tilde{\Theta}\sim\mathcal{U}([0,2\pi])\) cu \(tilde{R}\) și \(\tilde{\Theta}\) independente (ceea ce nu este adevărat în realitate). Vom vedea (printr-o ilustrație grafică) că această abordare este greșită (punctele sunt concentrate în centrul cercului). O funcție care să implementeze această abordare ar putea fi:
gen_unif_disc_wrong <- function(n = 10, R = 2, xc = 2, yc = 2){
r <- R*runif(n)
theta <- 2*pi*runif(n)
x <- xc + r*cos(theta)
y <- yc + r*sin(theta)
return(cbind(x, y))
}O abordare corectă este următoarea: căutăm să simulăm un cuplu de v.a. \((X,Y)\) care este uniform distribuit pe suprafața discului \(D\), i.e. densitatea cuplului este dată de \(f_{(X,Y)}(x,y)=\frac{1}{\pi L^2}\mathbf{1}_{D}(x,y)\). Considerând schimbarea de variabile în coordonate polare: \(x=r\cos(\theta)\) și \(y=r\sin(\theta)\), obiectivul este de a găsi densitatea variabilelor \(R\) și \(\Theta\) astfel încât \(X = R\cos(\Theta)\) și \(Y = R\sin(\Theta)\).
Fie \(g(x,y)=\left(\sqrt{x^2+y^2},\arctan(y/x)\right)=(r,\theta)\), transformarea pentru care avem \((R,\Theta)=g(X,Y)\). Știm că inversa acestei transformări este \(g^{-1}(r,\theta)=(r\cos(\theta),r\sin(\theta))\), prin urmare
\[ \begin{aligned} f_{(R,\Theta)}(r,\theta) &= f_{(X,Y)}\left(g^{-1}(r,\theta)\right)|\det(J_{g^{-1}}(r,\theta))|\\ &= \frac{1}{\pi L^2}\mathbf{1}_{D}(r\cos(\theta),r\sin(\theta))\left|\begin{array}{cc} \cos(\theta) & \sin(\theta)\\ r\sin(\theta) & -r\cos(\theta) \end{array}\right|\\ &= \frac{1}{\pi L^2} \mathbf{1}_{[0,L]}(r)\mathbf{1}_{[0,2\pi]}(\theta)r. \end{aligned} \]
Observăm că densitatea (marginală) a v.a. \(\Theta\) este
\[ \begin{aligned} f_{\Theta}(\theta) &= \int f_{(R,\Theta)}(r,\theta)\,dr = \mathbf{1}_{[0,2\pi]}(\theta)\int \frac{r}{\pi L^2} \mathbf{1}_{[0,L]}(r)\,d\theta\\ &= \frac{1}{\pi L^2} \mathbf{1}_{[0,2\pi]}(\theta) \frac{L^2}{2} = \frac{1}{2\pi} \mathbf{1}_{[0,2\pi]}(\theta), \end{aligned} \]
iar densitatea v.a. \(R\) este
\[ \begin{aligned} f_{R}(r) &= \int f_{(R,\Theta)}(r,\theta)\,d\theta = \frac{r}{\pi L^2} \mathbf{1}_{[0,L]}(r)\int_{0}^{2\pi}\,d\theta\\ &= \frac{r}{\pi L^2} \mathbf{1}_{[0,L]}(r)2\pi = \frac{2r}{L^2} \mathbf{1}_{[0,L]}(r). \end{aligned} \]
Din expresiile de mai sus putem observa că \(\Theta\) este o v.a. repartizată uniform pe \([0,2\pi]\) și putem verifica ușor că repartiția v.a. \(R\) este aceeași cu cea a v.a. \(L\sqrt{U}\) unde \(U\sim\mathcal{U}([0,1])\).
Astfel, pentru simularea unui punct \((X,Y)\) uniform pe \(D\) este suficient să simulăm o v.a. \(\Theta\) uniform pe \([0,2\pi]\) și o v.a. \(U\) uniformă pe \([0,1]\) și să luăm \(X=L\sqrt{U}\cos(\Theta)\) și \(Y=L\sqrt{U}\sin(\Theta)\). Funcția de mai jos implementează această metodă:
gen_unif_disc_good <- function(n = 10, R = 2, xc = 2, yc = 2){
r <- R*sqrt(runif(n))
theta <- 2*pi*runif(n)
x <- xc + r*cos(theta)
y <- yc + r*sin(theta)
return(cbind(x, y))
}Următoarea figură ne ilustrează cele două proceduri prezentate:
Generarea variabilelor aleatoare ce admit densitate
Metoda respingerii permite și simularea variabilelor aleatoare sau a vectorilor aleatori din repartițiile care admit densitate în raport cu măsura Lebesgue. Considerăm că vrem să generăm observații din vectorul aleator \(Z\) cu valori în \(\mathbb{R}^d\) care admite densitatea \(f\) (densitate țintă). Vom presupune că știm să simulăm un vector aleator \(X\) care admite densitatea \(g\) (densitate propusă sau propunere) și că există o constantă \(c\geq1\) care verifică relația \(f\leq cg\). Metoda respingerii propune să generăm un șir de vectori aleatori \((X_n)_{n\geq 1}\) independenți, de repartiție comună care admite ca densitate pe \(g\) și \((U_n)_{n\geq 1}\) un șir de variabile aleatoare independente (și independente și de \((X_n)_{n\geq 1}\)) și repartizate \(\mathcal{U}([0,1])\). Generăm punctele \(M_i=(X_i, cg(X_i)U_i)\) (care vor fi repartizate uniform pe hipograful lui \(cg\) din Propoziția 3) și ne oprim la primul indice \(i_0\) (aleator) care verifică \(cg(X_{i_0})U_{i_0}\leq f(X_{i_0})\) (conform Propoziția 1). Luăm \(Z = X_{i_0}\), iar acest vector aleator admite ca densitate pe \(f\) (conform Propoziția 2).
Justificarea algoritmului are la bază următoarele propoziții:
Propoziția 2 Fie \(f\) o densitate de probabilitate pe \(\mathbb{R}^d\) și considerăm hipograful lui \(f\)
\[ G=\left\{(x, y)\in\mathbb{R}^d\times\mathbb{R}\,|\,0\leq y\leq f(x)\right\}. \]
Fie \(M = (Z,Y)\) un vector aleator pe \(\mathbb{R}^d\times\mathbb{R}\) repartizat uniform pe \(G\). Atunci repartiția lui \(Z\) pe \(\mathbb{R}^d\) admite densitatea \(f\) în raport cu măsura Lebesgue \(\lambda_d\) pe \(\mathbb{R}^d\).
Înainte de a demonstra Propoziția 2 vom reaminti noțiunea de câmp de probabilitate produs. Fie \(\left(\Omega_1, \mathcal{F}_1, \mathbb{P}_1\right)\) și \(\left(\Omega_2, \mathcal{F}_2, \mathbb{P}_2\right)\) două câmpuri de probabilitate. Câmpul de probabilitate produs \(\left(\Omega, \mathcal{F}, \mathbb{P}\right)\) este definit prin
\[ \begin{aligned} & \Omega=\Omega_1 \times \Omega_2=\left\{\left(\omega_1, \omega_2\right) \mid \omega_1 \in \Omega_1, \omega_2 \in \Omega_2\right\}\\ & \mathcal{F}=\mathcal{F}_1 \otimes \mathcal{F}_2=\sigma\left(\left\{A_1 \times A_2 \mid A_1 \in \mathcal{F}_1, A_2 \in \mathcal{F}_2\right\}\right) \end{aligned} \]
și unica măsură de probabilitate \(\mathbb{P} = \mathbb{P}_1\otimes\mathbb{P}_2\) pe spațiul produs \(\left(\Omega, \mathcal{F}\right)\) care verifică
\[ \mathbb{P}\left(A_1 \times A_2\right)=\mathbb{P}_1\left(A_1\right) \times \mathbb{P}_2\left(A_2\right) \quad, \forall A_1 \in \mathcal{F}_1,\, A_2\in \mathcal{F}_2 \]
Mai mult, pentru orice \(E\in\mathcal{F}\) avem
\[ \begin{aligned} \mathbb{P}(E) & =\int \mathbb{P}_2\left(E_{\omega_1}\right) d \mathbb{P}_1\left(\omega_1\right) \\ & =\int \mathbb{P}_1\left(E_{\omega_2}\right) d \mathbb{P}_2\left(\omega_2\right) \end{aligned} \]
unde \(E_{\omega_1}\) și \(E_{\omega_2}\) sunt secțiunile lui \(E\) prin \(\omega_1\) respectiv \(\omega_2\), i.e.
\[ \begin{aligned} & E_{\omega_1}=\left\{\omega_2 \in \Omega_2 \mid\left(\omega_1, \omega_2\right) \in E\right\} \\ & E_{\omega_2}=\left\{\omega_1 \subset \Omega_1 \mid\left(\omega_1, \omega_2\right) \in E\right\}. \end{aligned} \]
Demonstrație. Vom considera pentru început cazul \(d=1\). Vrem să calculăm
\[ \mathbb{P}(Z \in[a, b]),\quad \forall [a, b] \subset \mathbb{R} \]
Avem că
\[ \mathbb{P}(Z \in[a, b])=\mathbb{P}(\underbrace{(Z, Y)}_M \in [a, b] \times \mathbb{R}) \]
și ținând cont că \(M\sim\mathcal{U}(G)\) rezultă că
\[ \mathbb{P}(Z \in[a, b])= \frac{\lambda_2(G \cap[a, b] \times \mathbb{R})}{\lambda_2(G)}. \]
Cum \(\lambda_2(G)=1\) obținem că \(\mathbb{P}(Z \in[a, b]) = \int_a^b f(x) dx\), \(\forall [a, b] \subset \mathbb{R}\) ceea ce implică că \(Z\sim f\).
Pentru cazul general \(d\), fie \(B\in\mathcal{B}_{\mathbb{R}^d}\) și ne propunem să calculăm \(\mathbb{P}(Z \in B)\). Cum \(M\sim\mathcal{U}(G)\) avem
\[ \mathbb{P}(Z \in B)=\mathbb{P}(\underbrace{(Z, Y)}_M \in B \times \mathbb{R}) = \frac{\lambda_{d+1}(G \cap B \times \mathbb{R})}{\lambda_{d+1}(G)}. \]
Dar \(\lambda_{d+1}(G) = 1\), prin urmare \(\mathbb{P}(Z \in B)=\lambda_{d+1}(G \cap B \times \mathbb{R})\). Fie \(G_{B} = G \cap B \times \mathbb{R}\) și ținând cont că \(\lambda_{d+1}=\lambda_d\otimes\lambda_1\) deducem
\[ \lambda_{d+1}(G_B)=\left(\lambda_d(\otimes) \lambda_1\right)(G_B) = \int_{\mathbb{R}^d} \lambda_1\left((G_B)_x\right) d \lambda_d(x). \]
Dar
\[ \begin{aligned} \left(G_B\right)_x & =\left\{y \in \mathbb{R} \mid(x, y) \in G_B\right\} \\ & =\{y \in \mathbb{R} \mid(x, y) \in G \cap B \times \mathbb{R}\} = \left\{\begin{array}{ll} [0, f(x)], & x\in B\\ \emptyset, & x \notin B \end{array}\right. \end{aligned} \]
de unde \(\lambda_1\left((G_B)_x\right) = f(x)\mathbf{1}_B(x)\). Astfel găsim că
\[ \mathbb{P}(Z \in B)=\int_{\mathbb{R}^d} \lambda_1\left((G_B)_x\right) d \lambda_d(x) = \int_{\mathbb{R}^d} f(x)\mathbf{1}_B(x) d \lambda_d(x) = \int_{B} f(x)d \lambda_d(x) \]
și din unicitatea măsurilor de probabilitate obținem că \(Z\) admite densitatea \(f\) în raport cu \(\lambda_d\).
Propoziția 3 Fie \(X\) un vector aleator pe \(\mathbb{R}^d\) cu densitatea de repartiție \(g\) și \(U\sim\mathcal{U}([0,1])\) independent de \(X\). Considerăm punctul \(M = (X, cg(X)U)\), cu \(c>0\), și fie \(H\) hipograful lui \(cg\), i.e.
\[ H=\left\{(x, y)\in\mathbb{R}^d\times\mathbb{R}\,|\,0\leq y\leq cg(x)\right\}. \]
Atunci punctul \(M\sim\mathcal{U}(H)\).
Demonstrație. Pentru a identifica repartiția vectorului \(M:=(X, c g(X) U)\), vom calcula \(\mathbf{P}(M \in A \times B)\) pentru \(A \in \mathcal{B}_{\mathbb{R}^{d}}\) și \(B \in \mathcal{B}_{\mathbb{R}^{d}}\) oarecare. Cum \(M\) este o funcție măsurabilă care depinde de cuplul \((X, U)\), vom scrie această probabilitate în raport cu densitatea \(h\) a acestui cuplu care din independența variabilelelor aleatoare \(X\) și \(U\), se scrie drept \(h(x, u)= g(x) \mathbf{1}_{[0,1]}(u)\). Astfel avem
\[ \begin{aligned} \mathbf{P}(M \in A \times B) & = \int_{\mathbb{R}^{d} \times \mathbb{R}} \mathbf{1}_{A \times B}(x, c g(x) u) h(x, u) \mathrm{d}\lambda_{d+1}(x, u)\\ & =\int_{\mathbb{R}^{d} \times \mathbb{R}} \mathbf{1}_{A \times B}(x, c g(x) u) g(x) \mathbf{1}_{[0,1]}(u) \mathrm{d}\left(\lambda_{d} \otimes \lambda_{1}\right)(x, u) \\ & =\int_{\mathbb{R}^{d}} \mathbf{1}_{A}(x)\left\{\int_{\mathbb{R}} \mathbf{1}_{B}(c g(x) u) g(x) \mathbf{1}_{[0,1]}(u) \mathrm{d} \lambda_{1}(u)\right\} \mathrm{d} \lambda_{d}(x) \end{aligned} \]
Fie \(I(x) = \int_{\mathbb{R}} \mathbf{1}_{B}(c g(x) u) g(x) \mathbf{1}_{[0,1]}(u) \mathrm{d} \lambda_{1}(u)\). Dacă \(g(x)=0\) atunci \(I(x)=0\) iar în caz contrar, dacă \(g(x)>0\) putem schimba variabila \(t=c g(x) u\) cu \(x\) fixat și obținem
\[ \begin{aligned} I(x) &=\int_{\mathbb{R}} \mathbf{1}_{B}(t) g(x) \mathbf{1}_{[0,1]}\left(\frac{t}{c g(x)}\right) \frac{1}{c g(x)} \mathrm{d} \lambda_{1}(t) \\ & =\frac{1}{c} \int_{\mathbb{R}} \mathbf{1}_{B}(t) \mathbf{1}_{[0, c g(x)]}(t) \mathrm{d} \lambda_{1}(t) \\ & =\frac{1}{c} \int_{\mathbb{R}} \mathbf{1}_{B \cap[0, c g(x)]}(t) \mathrm{d} \lambda_{1}(t) \\ & =\frac{1}{c} \lambda_{1}(B \cap[0, c g(x)]) \end{aligned} \]
Remarcăm, de asemenea, că dacă \(g(x)=0\) atunci \(B \cap[0, c g(x)]\) este sau \(\emptyset\) sau\(\{0\}\), ambele de măsură Lebesgue nulă, astfel relația de mai sus este valabilă și pentru cazul \(g(x)=0\). Prin urmare găsim că
\[ \mathbf{P}(M \in A \times B)=\frac{1}{c} \int_{\mathbb{R}^{d}} \mathbf{1}_{A}(x) \lambda_{1}(B \cap[0, c g(x)]) \mathrm{d} \lambda_{d}(x). \]
Pentru a compara această probabilitate cu \(\mu(A \times B)\), unde \(\mu\) reprezintă repartiția uniformă pe \(H\), să exprimăm această din urmă relație conform definiției
\[ \begin{aligned} \mu(A \times B)=\frac{\lambda_{d+1}((A \times B) \cap H)}{\lambda_{d+1}(H)} & =\frac{1}{c}\left(\lambda_{d} \otimes \lambda_{1}\right)((A \times B) \cap H) \\ & =\frac{1}{c} \int_{\mathbb{R}^{d}} \lambda_{1}\left(((A \times B) \cap H)_{x}\right) \mathrm{d} \lambda_{d}(x) \end{aligned} \]
unde am ținut seama că \(\lambda_{d+1}(H) = \frac{1}{c}\) și unde \(((A \times B) \cap H)_{x}\) este secțiunea prin \(x\) a mulțimii \((A \times B) \cap H\). Secțiunea este dată de
\[ \begin{aligned} ((A \times B) \cap H)_{x} & =\{y \in \mathbb{R} \mid(x, y) \in(A \times B) \cap H\} \\ & =\{y \in \mathbb{R} \mid x \in A, y \in B \cap[0, c g(x)]\} \\ & = \begin{cases}\emptyset & \text { dacă } x \notin A, \\ B \cap[0, c g(x)] & \text { dacă } x \in A .\end{cases} \end{aligned} \]
În consecință
\[ \lambda_{1}\left(((A \times B) \cap H)_{x}\right)=\lambda_{1}(B \cap[0, c g(x)]) \mathbf{1}_{A}(x), \]
care arată că
\[ \mu(A \times B)= \frac{1}{c} \int_{\mathbb{R}^{d}} \lambda_{1}(B \cap[0, c g(x)]) \mathbf{1}_{A}(x) \mathrm{d} \lambda_{d}(x) \]
de unde
\[ \forall A \in \mathcal{B}_{\mathbb{R}^{d}}, \forall B \in \mathcal{B}_{\mathbb{R}}, \quad P_{M}(A \times B):=\mathbf{P}(M \in A \times B)=\mu(A \times B). \]
Am arătat că măsurile finite \(P_{M}\) și \(\mu\) coincid pe clasa dreptunghiurilor \(A \times B\) (care este un \(\pi\)-sistem), prin urmare din teorema de unicitate a măsurilor ele coincid pe \(\sigma\)-algebra generată \(\sigma(\mathcal{R})=\mathcal{B}_{\mathbb{R}^{d}} \otimes \mathcal{B}_{\mathbb{R}}\), pe care o indentificăm cu \(\mathcal{B}_{\mathbb{R}^{d+1}}\). Astfel \(P_{M}=\mu\), i.e. repartiția lui \(M\) este repartiția uniformă pe \(H\).
Ca aplicație a rezultatelor de mai sus considerăm o serie de exerciții:
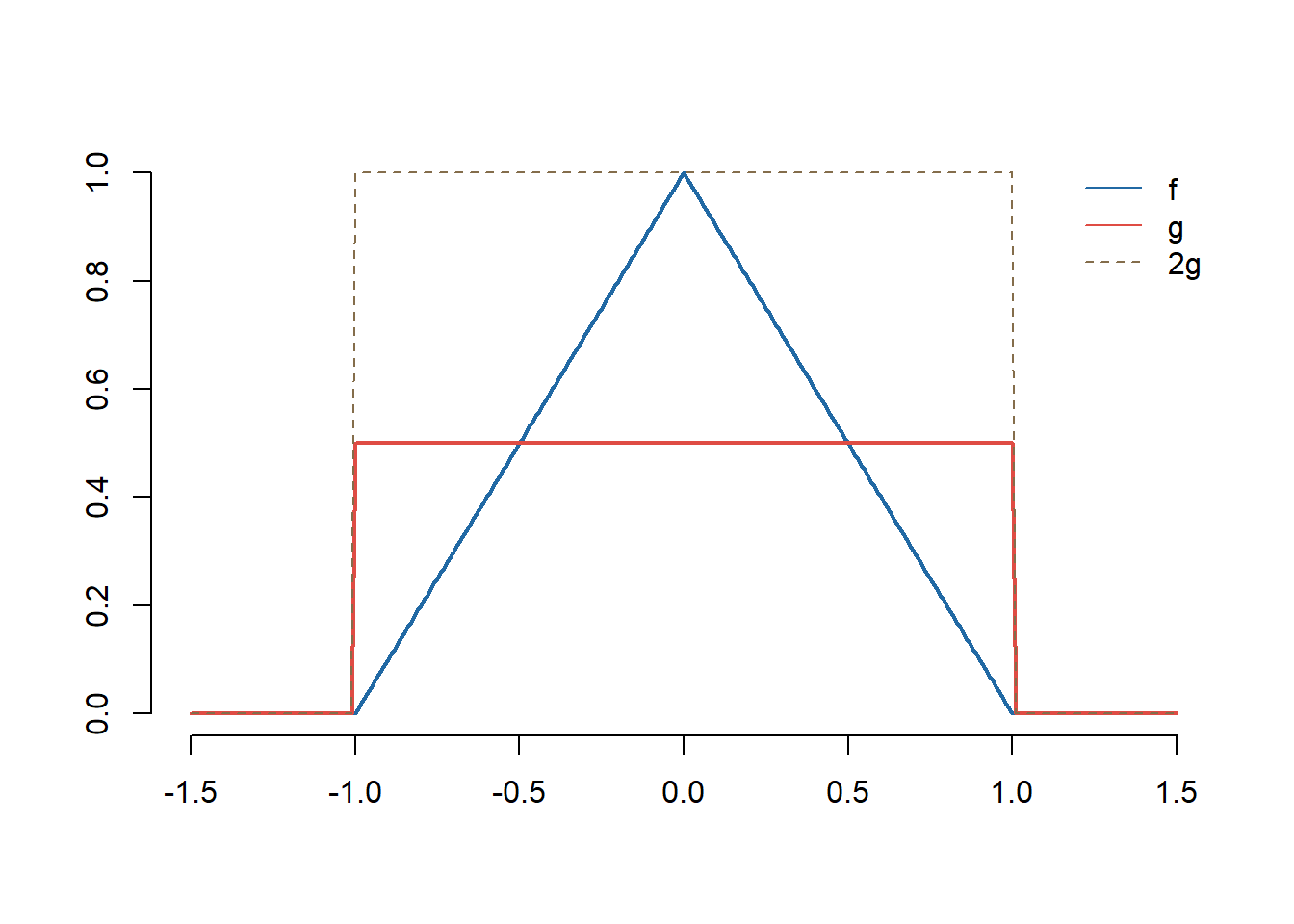
Exercițiul 14 (Repartiția triunghiulară) Folosind metoda respingerii, propuneți o metodă de simulare pentru observații independente din densitatea de repartiție \(f:x\mapsto (1-|x|)^+\).
Soluție. Observăm că pentru toți \(x\in\mathbb{R}\) avem
\[ f(x) \leq \mathbf{1}_{\{x\in [-1, 1]\}} = 2 g(x), \]
unde \(g(x) = \frac{1}{2}\mathbf{1}_{\{x\in [-1, 1]\}}\) este densitatea repartiției uniforme pe \([-1,1]\).
Pentru a simula din repartiția \(f\) procedăm astfel
simulăm \(X\) repartizată \(\mathcal{U}[-1,1]\) (\(X = 2V-1\) cu \(V\sim\mathcal{U}(0,1)\))
simulăm \(U\sim\mathcal{U}(0,1)\)
repetăm procedeul până când \(2Ug(X)\leq f(X)\).
Următorul cod implementează acest algoritm:
f <- function(x){
return(ifelse(abs(x)<=1, 1-abs(x), 0))
}
g <- function(x){
return(ifelse(abs(x)<=1, 0.5, 0))
}
sim_f <- function(n = 1000){
x <- rep(0, n)
for (i in 1:n){
# gen obs din g
x[i] <- runif(1, -1, 1)
# gen uniforma
u <- runif(1)
while(2*u*g(x[i]) > f(x[i])){
x[i] <- runif(1, -1, 1)
u <- runif(1)
}
}
return(x)
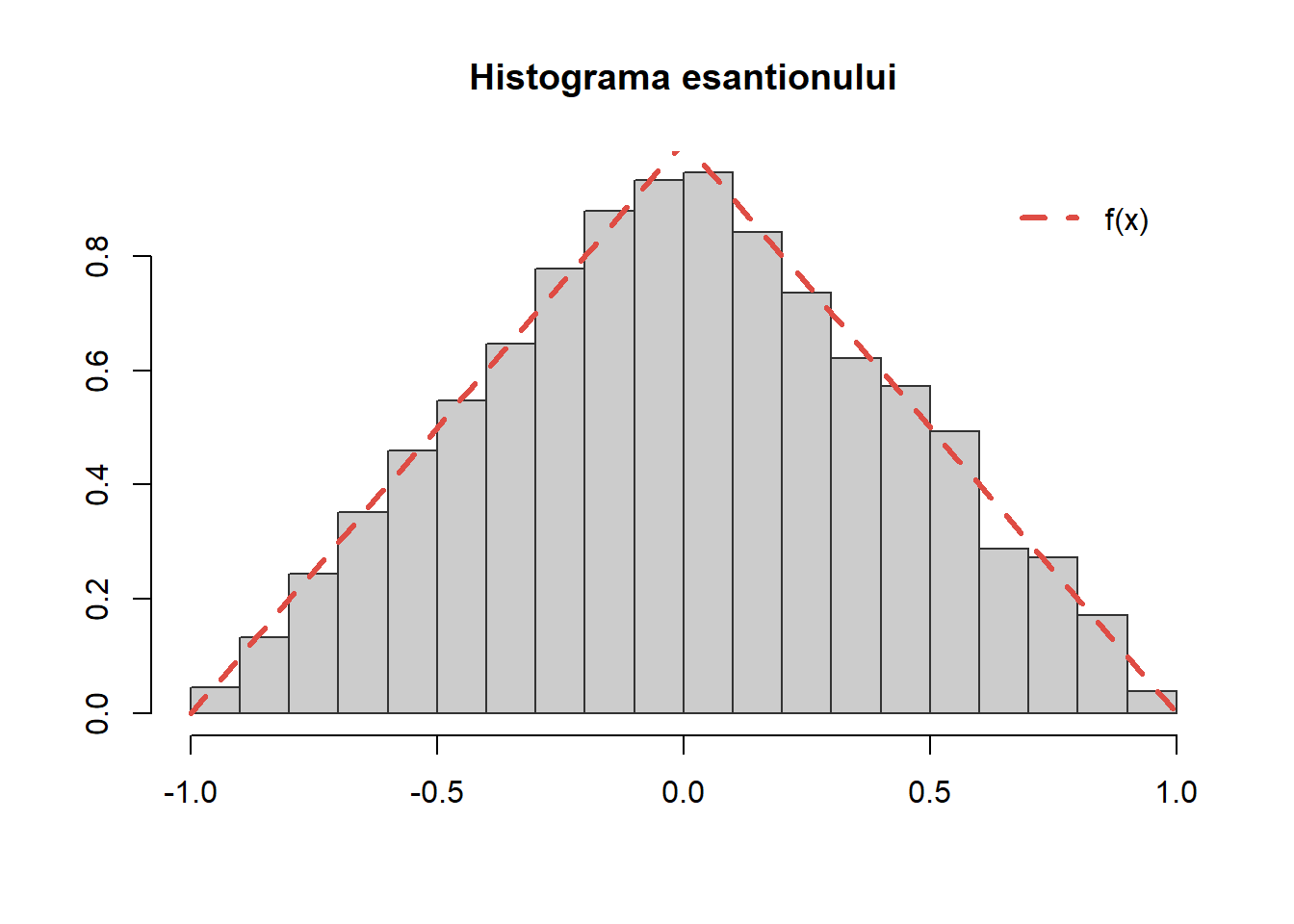
}Putem valida algoritmul propus trasând histograma unui eșantion de volum \(10000\) și suprapunând densitatea \(f\):
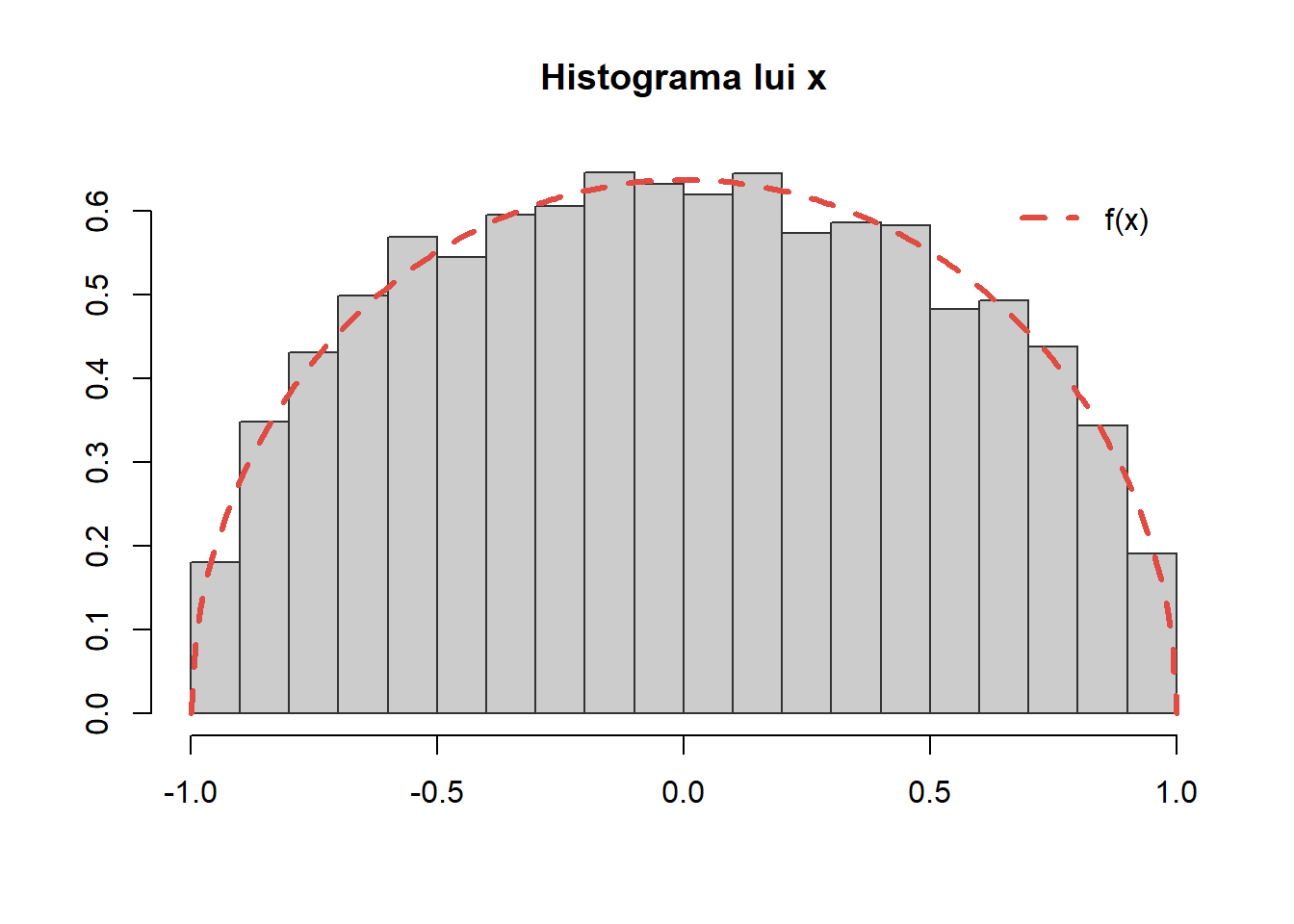
Exercițiul 15 (Repartiția semicirculară a lui Wigner3) Fie \(f\) densitatea de repartiție definită prin
\[ f(x) = \frac{2}{\pi}\sqrt{1-x^2}\mathbf{1}_{[-1,1]}(x) \]
- Folosiți metoda respingerii pentru a genera \(10000\) de observații repartizate cu densitatea \(f\).
- Trasați histograma acestui eșantion și comparați cu densitatea \(f\).
Soluție. Pentru primul punct avem:
- Observăm că
\[ f(x) \leq \frac{2}{\pi}\mathbf{1}_{[-1,1]}(x) = \frac{4}{\pi}g(x) \]
unde \(g(x) = \frac{1}{2}\mathbf{1}_{[-1,1]}(x)\) este densitatea repartiției uniforme pe \([-1,1]\). Astfel metoda respingerii sugerează următorul algoritm:
f <- function(x){
return(2/pi * sqrt(1-x^2)*(abs(x) <= 1))
}
sim_f <- function(n){
x <- rep(0, n)
for (i in 1:n){
# generam obs din g
x[i] <- runif(1, -1, 1)
# generam uniforma
u <- runif(1)
while(u > pi * f(x[i])/2){
x[i] <- runif(1, -1, 1)
u <- runif(1)
}
}
return(x)
}Putem îmbunătății codul de mai sus (vrem să evităm să avem și bucla for și bucla while imbricate) dacă ținem cont de faptul că probabilitatea de acceptare este \(p = \frac{\pi}{4}\) iar pentru a genera un eșantion de \(m\) observații avem nevoie, în medie, de \(\frac{m}{p}\) simulări. Avem
sim_f2 <- function(n){
out <- c() # esantionul final
# cate obs mai avem de generat
m <- n
# cat timp nu avem esantionul de talia dorita
# continuam procedeul
while (m>0){
# simulam m/p observatii
x <- runif((4*m)%/%pi + 1, -1, 1)
u <- runif((4*m)%/%pi + 1)
# testam care obs sunt acceptate
y <- (u <= pi * f(x)/2)
# pastram doar punctele acceptate
out <- c(out, x[which(y)])
m <- n - length(out)
}
return(out[1:n])
}Putem compara cele două metode, în funcție de timpul de execuție (și observăm că în fapt a doua metodă este mai lentă):
n <- 10000
# Metoda 1
start <- proc.time()
x <- sim_f(n)
proc.time() - start user system elapsed
0.03 0.00 0.03 # Metoda 2
star <- proc.time()
x <- sim_f2(n)
proc.time() - start user system elapsed
0.05 0.00 0.04 - Putem valida algoritmul propus prin metoda respingerii trasând histograma eșantionului:
Exercițiul 16 (Repartiția normală - metoda respingerii 1) Plecând cu o propunere de tip \(\mathrm{Exp}(\lambda)\) vrem să generăm, cu ajutorul metodei acceptării-respingerii, un eșantion din următoarea densitate (jumătate de normală):
\[ f(x) = \left\{\begin{array}{ll} \frac{2}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}, & \mbox{dacă $x\geq0$}\\ 0, & \mbox{altfel}\\ \end{array}\right. \]
Cum putem modifica algoritmul pentru a genera un eșantion dintr-o repartiție normală standard?
Soluție. Pentru început, să observăm că densitatea țintă \(f\) corespunde lui \(|X|\), unde \(X\sim\mathcal{N}(0,1)\). Alternativ se poate interpreta drept densitatea unei normale standard \(X\sim\mathcal{N}(0,1)\) condiționată la \(X>0\).
Fie \(g\) densitatea repartiției exponențiale de parametru \(\lambda\),
\[ g(x) = \left\{\begin{array}{ll} \lambda e^{-\lambda x}, & \mbox{dacă $x\geq0$}\\ 0, & \mbox{altfel}\\ \end{array}\right. \]
Pentru a aplica algoritmul de acceptare-respingere trebuie să găsim valoarea lui \(c>0\) pentru care \(f(x)\leq c g(x)\) pentru toate valorile \(x\in \mathbb{R}\). Pentru \(x\geq0\) avem
\[ \frac{f(x)}{g(x)}=\frac{2}{\lambda\sqrt{2\pi}}e^{-\frac{x^2}{2}+\lambda x} \]
și cum funcția \(-\frac{x^2}{2}+\lambda x\) își atinge valoarea maximă în punctul \(x=\lambda\) rezultă că
\[ \frac{f(x)}{g(x)}\leq c^*, \,\,\forall x \geq0 \]
unde
\[ c^*=\sqrt{\frac{2}{\pi\lambda^2}}e^{\lambda^2/2}. \]
Astfel algoritmul devine:
pentru \(n=1,2,\dots\)
generează \(X_n\sim Exp(\lambda)\)
generează \(U_n\sim\mathcal{U}[0,1]\)
dacă \(U_n\leq\exp\left(-\frac{1}{2}(X_n-\lambda)^2\right)\) atunci
întoarceți \(X_n\)
Avem funcția:
# generarea punctelor din densitatea f
f <- function(x) {
return((x> 0) * 2 * dnorm(x,0,1))
}
g <- function(x) { return(dexp(x,1)) }
c_star <- sqrt(2 * exp(1) / pi)
rhalfnormal <- function(n) {
res <- numeric(length=n)
i <- 0
while (i<n) {
U <- runif(1, 0, 1)
X <- rexp(1, 1)
if (c_star * g(X) * U <= f(X)) {
i <- i+1
res[i] <- X
}
}
return(res)
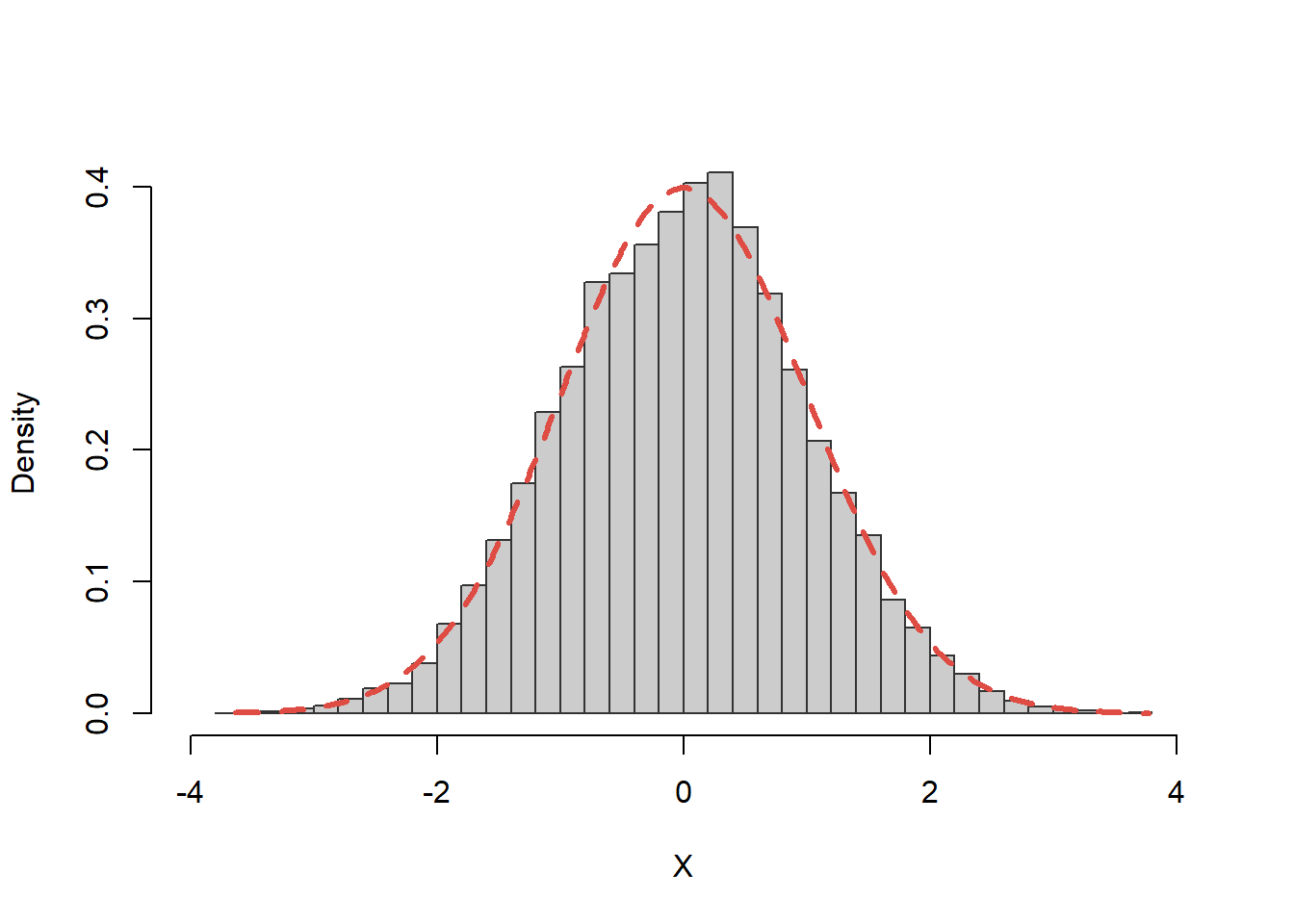
}Pentru a testa validitatea algoritmului vom trasa histograma unui eșantion de volum \(n=10000\) peste care suprapunem densitatea de repartiție teoretică:
Cum densitatea \(f\) este densitatea unei normale standard \(X\sim\mathcal{N}(0,1)\) condiționată la \(X>0\) și cum densitatea normală este simetrică față de medie (0 în acest caz) algoritmul se modifică acceptând \(X_n\) și \(-X_n\) cu probabilitatea de \(0.5\).
Astfel avem funcția:
f2 <- function(x) {
return(dnorm(x,0,1))
}
normal1 <- function(n) {
res <- numeric(length=n)
i <- 0
while (i<n) {
U <- runif(1, 0, 1)
X <- rexp(1, 1)
if (c_star * g(X) * U <= f(X)) {
i <- i+1
res[i] <- ifelse(runif(1) <= 0.5, X, -X);
}
}
return(res)
}Verificăm dacă algoritmul este valid prin generarea unui eșantion de volum \(n=10000\), trasarea histogramei corespunzătoare peste care suprapunem densitatea de repartiție teoretică:
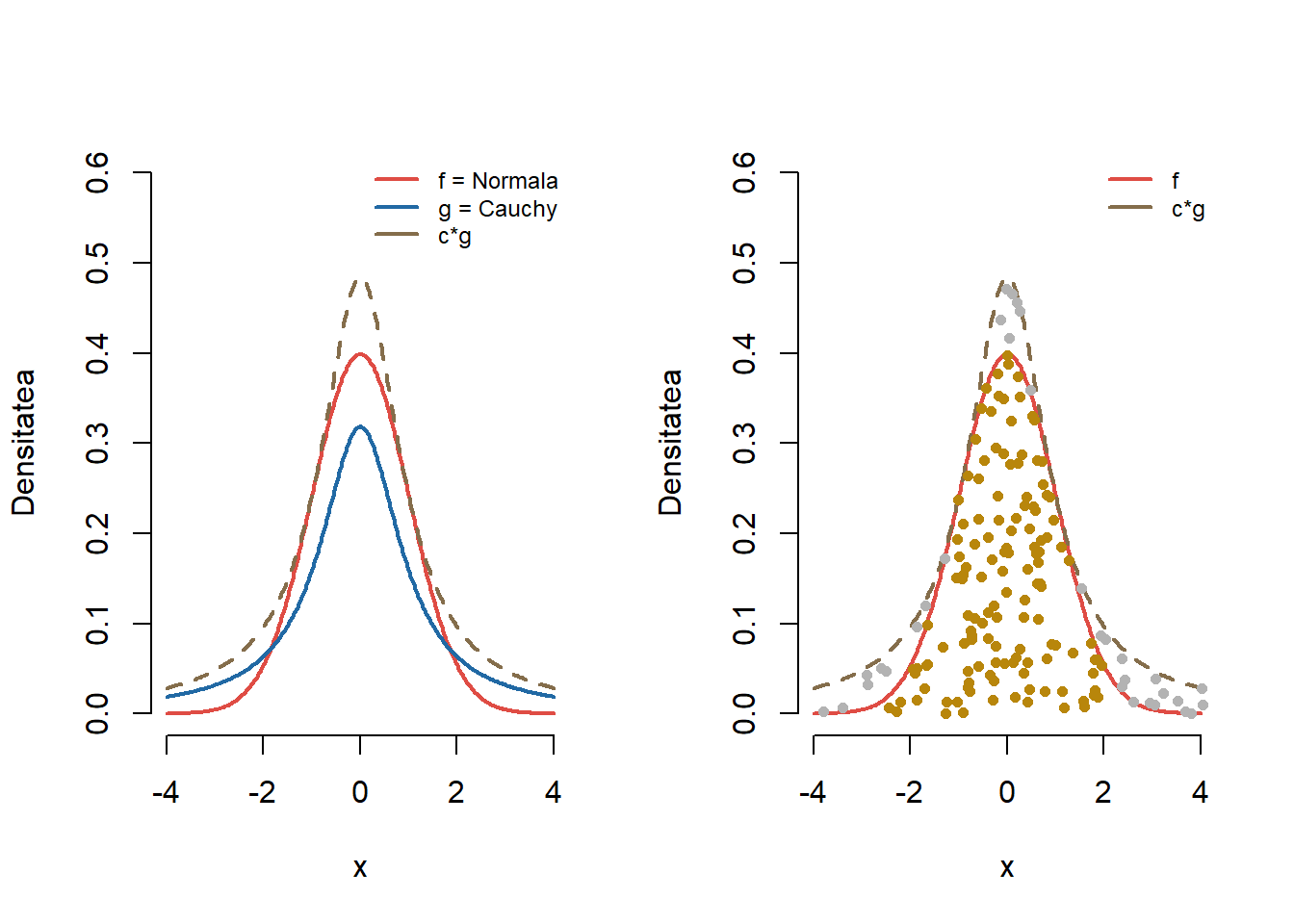
Exercițiul 17 (Repartiția normală - metoda respingerii 2) Plecând cu o propunere de tip Cauchy \(C(0, 1)\) vrem să generăm, cu ajutorul metodei acceptării-respingerii, un eșantion de volum \(n\) dintr-o populație normală standard. Descrieți metoda și algoritmul aferent.
Soluție. Fie \(g\) densitatea repartiției Cauchy \(C(0, 1)\) (repartiția propunere),
\[ g(x) = \frac{1}{\pi} \frac{1}{1+x^2},\quad \forall x\in\mathbb{R}. \]
Pentru a aplica algoritmul de acceptare-respingere trebuie să găsim valoarea lui \(c>0\) pentru care \(f(x)\leq c g(x)\) pentru toate valorile \(x\in \mathbb{R}\), unde \(f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\) este densitatea de repartiție a repartiției \(\mathcal{N}(0,1)\). Pentru \(x\in\mathbb{R}\) avem
\[ \frac{f(x)}{g(x)}=\sqrt{\frac{\pi}{2}}(1+x^2)e^{-\frac{x^2}{2}} \]
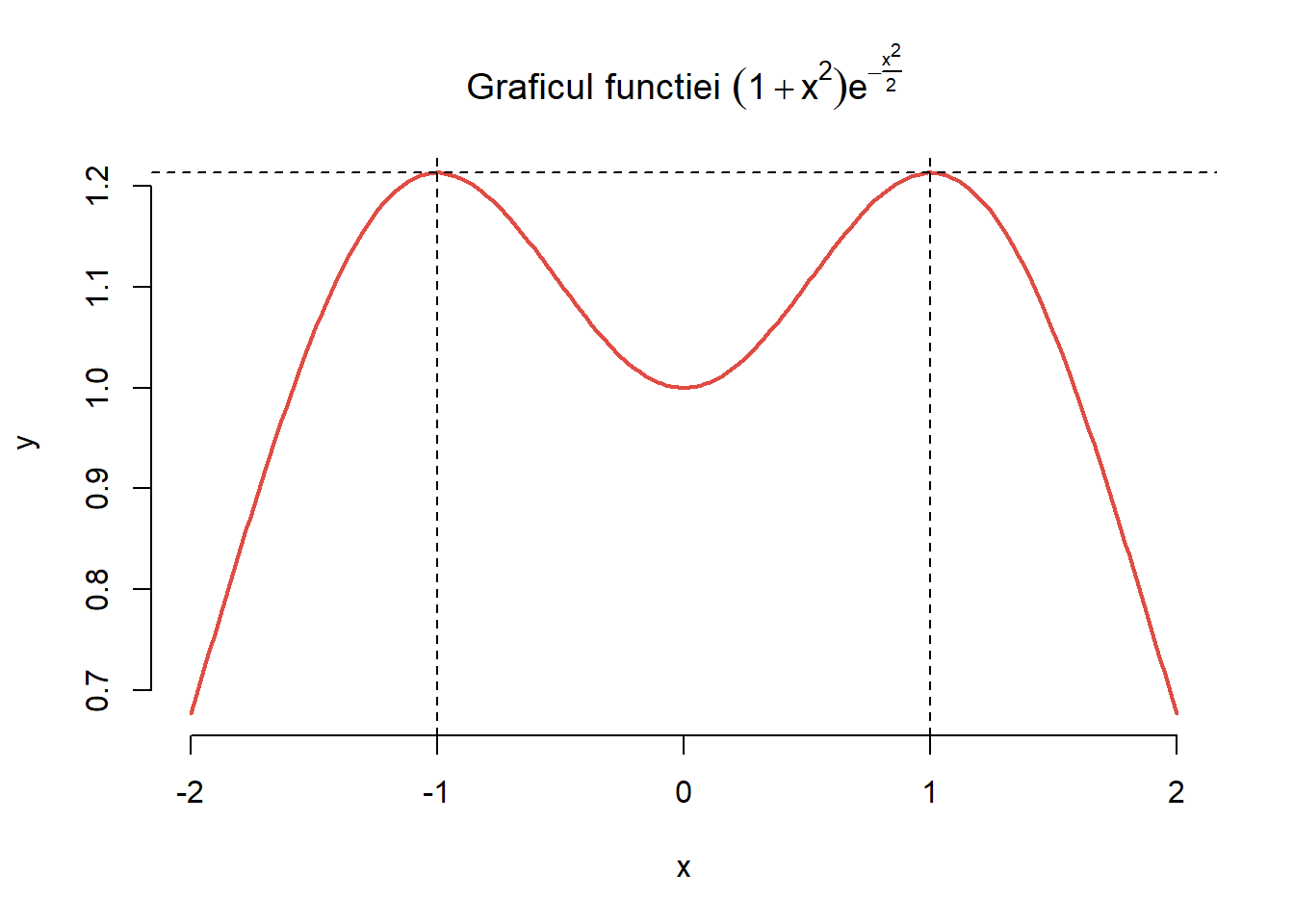
și cum funcția \((1+x^2)e^{-\frac{x^2}{2}}\) își atinge valoarea maximă în punctele \(x=\pm 1\) (maxim care este egal cu \(\frac{2}{\sqrt{e}}\)) după cum putem observa și în figura de mai jos
rezultă că
\[ \frac{f(x)}{g(x)}\leq c^*, \,\,\forall x \in \mathbb{R} \]
unde \(c^*=\sqrt{\frac{\pi}{2}}\frac{2}{\sqrt{e}} = \sqrt{\frac{2\pi}{e}}\).
Astfel algoritmul devine:
pentru \(n=1,2,\dots\)
generează \(X_n\sim C(0,1)\) folosind metoda inversă din Exercițiul 9
generează \(U_n\sim\mathcal{U}[0,1]\)
dacă \(c^* U_n g(X_n)\leq f(X_n)\) atunci
returnați \(X_n\)
Avem funcția:
# generarea punctelor din densitatea normala
f <- function(x) {
return(dnorm(x,0,1))
}
g <- function(x) {return(dcauchy(x, 0, 1)) }
c_star <- sqrt(2 * pi / exp(1))
gen_normal_cauchy <- function(n) {
out <- numeric(n)
i <- 0
while (i<n) {
U <- runif(1, 0, 1)
X <- tan(pi*(runif(1) - 0.5))
# alternativ
# X <- rcauchy(1, 0, 1)
if (c_star * g(X) * U <= f(X)) {
i <- i+1
out[i] <- X
}
}
return(out)
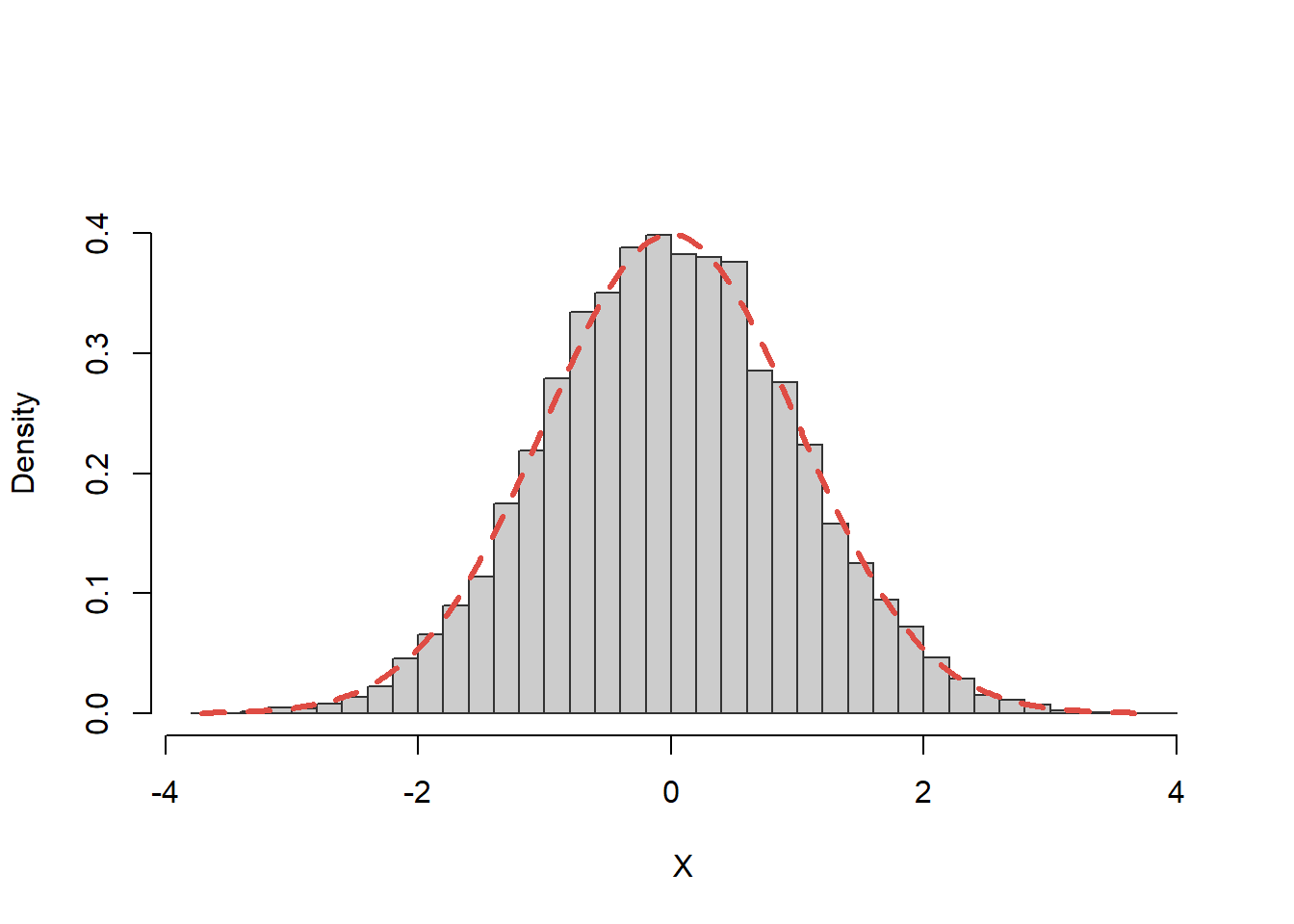
}Pentru a testa validitatea algoritmului vom trasa histograma unui eșantion de volum \(n=10000\) peste care suprapunem densitatea de repartiție teoretică:
Generarea variabilelor aleatoare discrete
Metoda respingerii nu se limitează doar la acele repartiții care admit densitate de repartiție, ea poate fi aplicată și în cazul repartițiilor discrete. Vom presupune, pentru simplificarea notațiilor, că repartițiile discrete pe care le considerăm iau valori într-o submulțime a numerelor naturale \(\mathbb{N}\) (în orice caz, o repartiție discretă ia valori într-o mulțime ce poate fi pusă în bijecție cu o submulțime a lui \(\mathbb{N}\)).
Astfel, ne propunem să simulăm observații dintr-o variabilă aleatoare \(Z\) a cărei repartiție este dată de \(Z(\Omega)\subset\mathbb{N}\) și de funcția de masă \(f:\mathbb{N}\to [0,1]\) cu \(f(k)=p_k=\mathbb{P}(Z=k)\). Pentru aceasta presupunem că știm să simulăm o variabilă aleatoare discretă \(X\), pentru care \(X(\Omega)\subset\mathbb{N}\) iar funcția de masă \(g:\mathbb{N}\to [0,1]\) este \(g(k)=q_k=\mathbb{P}(X=k)\) și verifică \(f\leq cg\) pentru un \(c\geq 1\) (aici considerăm că \(Z(\Omega)\subset X(\Omega)\)).
Propoziția 4 Folosind notațiile de mai sus, fie \((\Omega, \mathcal{F}, \mathbb{P})\) un câmp de probabilitate și \((X_n)_n\) un șir de variabile aleatoare independente de aceeași repartiție cu \(X\) și \((U_n)_n\) un șir de variabile aleatoare i.i.d. repartizate \(\mathcal{U}([0,1])\), cele două șiruri fiind și independente între ele. Definim variabila aleatoare \(T\) prin
\[ T(\omega) = \inf\{n\in\mathbb{N}^{*}\,|\,cg(X_n(\omega))U_n(\omega)\leq f(X_n(\omega))\} \]
adoptând convenția \(\inf\emptyset = \infty\) și \(X_{T}:\Omega\to\mathbb{R}^d\) prin
\[ X_{T}(\omega)=\left\{\begin{array}{ll} X_{T(\omega)}(\omega), & T(\omega)<\infty\\ 0, & T(\omega) = \infty \end{array}\right. \]
Atunci \(X_T\) este o variabilă aleatoare discretă cu aceeași repartiție ca \(Z\), i.e. \(\mathbb{P}(X_T=k)=f(k),\quad\forall k\in\mathbb{N}\).
Algoritmul de respingere se scrie succint astfel:
Generăm o observație din \(X\) cu funcția de masă \(q_k\).
Generăm o observație \(U\sim\mathcal{U}(0,1)\).
Dacă \(U < \frac{p_k}{cq_k}\) atunci \(Z = X\) altfel mergem la pasul 1 și repetăm.
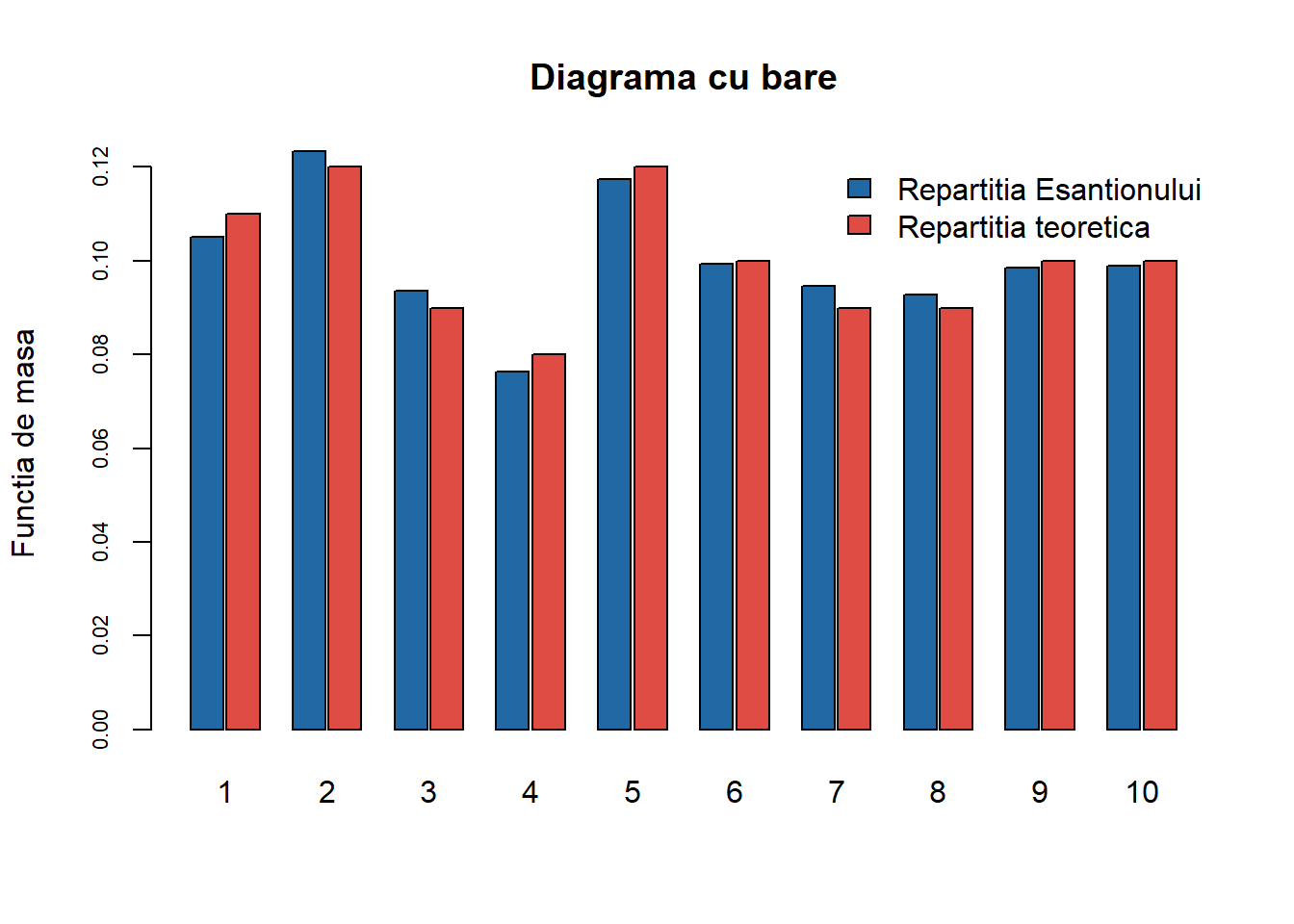
Exercițiul 18 Folosind metoda respingerii, propuneți un algoritm de simulare a unui eșantion de \(n = 1000\) de observații independente din variabila aleatoare
\[ Z\sim\left(\begin{array}{cccccccccc} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10\\ 0.11 & 0.12 & 0.09 & 0.08 & 0.12 & 0.10 & 0.09 & 0.09 & 0.10 & 0.10 \end{array}\right) \]
Soluție. Am văzut deja în Exercițiul 4 o soluție pentru această problemă dar acum vom rezolva problema folosind metoda respingerii. Pentru aceasta vom considera că știm să generăm observații independente dintr-o variabilă aleatoare \(X\sim\mathcal{U}(\{1,2,\ldots,10\})\), adică \(q_k = \frac{1}{10}\) pentru \(k\in\{1,2,\ldots,10\}\). Pentru această alegere a lui \(X\), respectiv \(q_k\), putem alege constanta \(c\) astfel încât
\[ c = \max_{k}\frac{p_k}{q_k} = 10\max_{k}p_k = 10\times 0.12 = 1.2. \]
Algoritmul devine astfel:
- Generăm \(X\sim\mathcal{U}(\{1,2,\ldots,10\})\) (de exemplu folosind relația din Secțiunea 0.3.1.1, \(X = [10U_1] + 1\) cu \(U_1\sim\mathcal{U}(0,1)\))
- Generăm \(U\sim\mathcal{U}(0,1)\)
- Dacă \(Ucg(X)\leq f(X)\) atunci \(Z=X\) altfel trecem la pasul 1
Relația din pasul 3 se rescrie sub forma
\[ U\times 1.2\times \frac{1}{10}\leq f(X) \iff U\leq \frac{f(X)}{0.12} \] Următoarea funcție implementează acest procedeu:
pX <- c(0.11, 0.12, 0.09, 0.08, 0.12,
0.1, 0.09, 0.09, 0.1, 0.1)
gen_MR_X <- function(n, pX = pX){
lx <- length(pX)
m <- 0
x <- rep(0, n)
# determinam constanta
c1 <- lx*max(pX)
m1 <- max(pX)
i <- 0
while(m <= n){
y <- sample(1:lx, 1, replace = TRUE, prob = rep(1/lx, lx))
u <- runif(1)
i <- i+1 # nr obs gen
if (u <= pX[y]/m1){
m <- m + 1
x[m] <- y
}
}
return(list(x = x,
nr_iter = i,
nr_med = c1*n))
}Să observăm că acest algoritm necesită în medie \(1.2\) iterații (în general \(c\) iterații) pentru genera o observație din \(Z\). Putem testa acest lucru pentru \(n = 100\) observații:
N1 <- rep(0, 100)
for (i in 1:100){
x <- gen_MR_X(n = 100, pX = pX)
N1[i] <- x$nr_iter
}
mean(N1)[1] 121.57Putem compara repartiția empirică cu cea teoretică:
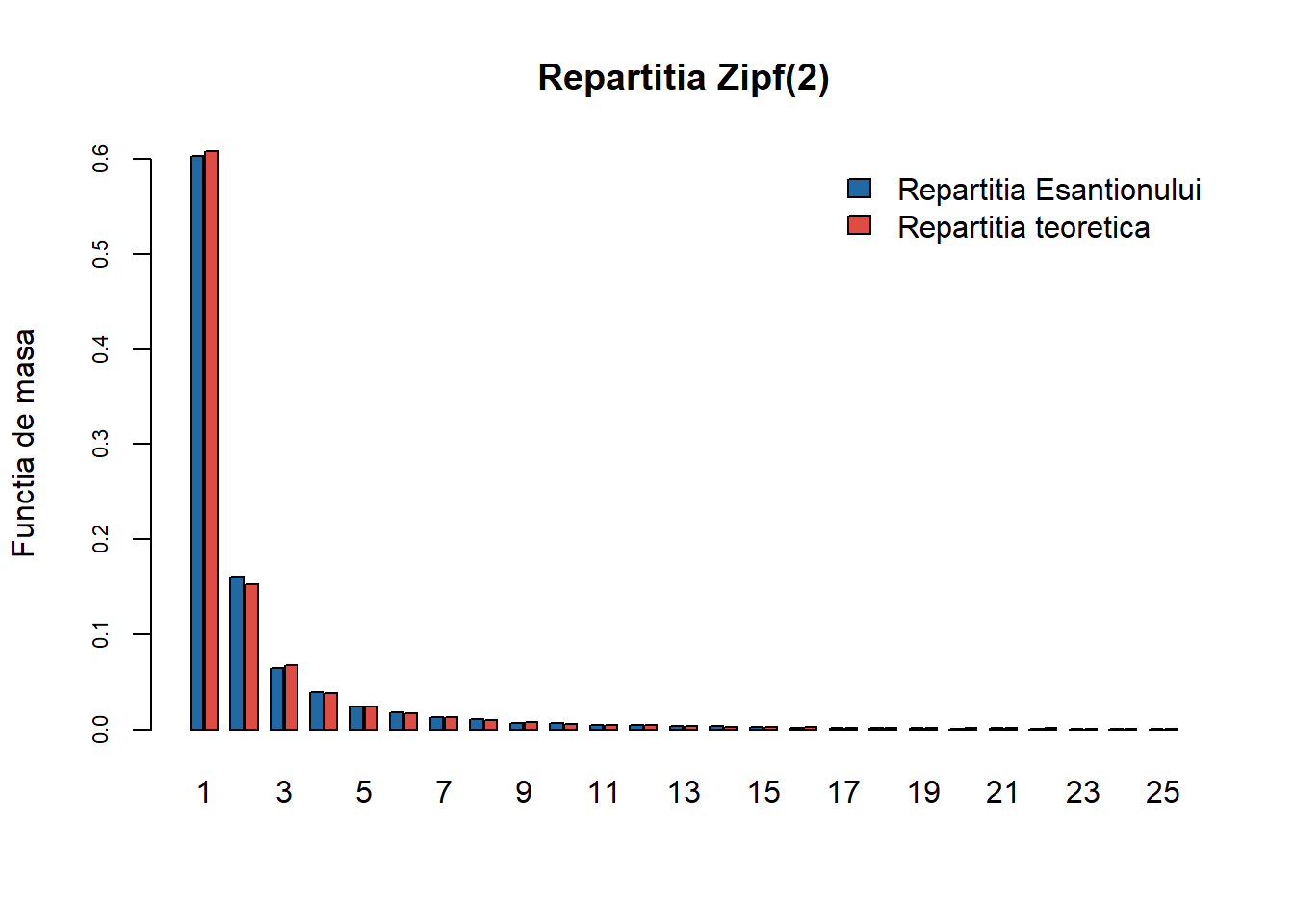
Exercițiul 19 (Repartiția Zipf) Folosind metoda respingerii generați \(n = 1000\) de observații din repartiția \(\mathrm{Zipf}(2)\).
Soluție. Repartiția Zipf este folosită cu precădere în lingvistică și științele sociale dar nu numai. Reamintim că o variabilă aleatoare \(Z\) repartizată \(\mathrm{Zipf}(a)\), are suportul pe mulțimea \(\mathbb{N}^*\) și funcția de masă dată de
\[ \mathbb{P}(Z = k) = \frac{1}{\zeta(a)k^a}, \quad k\in \mathbb{N}^* \]
unde \(\zeta(a) = \sum_{k\geq1}\frac{1}{k^a}\) este funcția \(\zeta\) a lui Riemann.
Vom considera cazul \(a=2\). În acest caz știm că \(\zeta(2) = \sum_{k\geq1}\frac{1}{k^2} = \frac{\pi^2}{6}\) prin urmare
\[ f(k) = p_k = \frac{6}{\pi^2 k^2}, \quad k\geq1. \]
Vom folosi ca propunere repartiția cu funcția de masă
\[ g(k) = q_k = \frac{1}{k(k+1)}, \quad k\geq1. \]
Alegem această propunere deoarece este ușor de simulat din ea, mai precis dacă luăm \(U\sim\mathcal{U}(0,1)\) avem
\[ \begin{aligned} q_k &= \frac{1}{k(k+1)} = \frac{1}{k} - \frac{1}{k+1} = \mathbb{P}\left(\frac{1}{k+1}< U\leq \frac{1}{k}\right)\\ &= \mathbb{P}\left(k\leq \frac{1}{U}< k+1\right) \end{aligned} \]
ceea ce arată că variabila aleatoare \(X=\left[\frac{1}{U}\right]\) are funcția de masă \(q_k\). În plus, putem determina cu ușurință constanta \(c\) care verifică
\[ c = \sup_{k}\frac{p_k}{q_k} = \frac{6}{\pi^2}\sup_{k}\frac{k+1}{k} = \frac{12}{\pi^2}. \]
Algoritmul devine:
- Generăm \(X\) cu repartiția \(q_k\): luăm \(U\sim\mathcal{U}(0,1)\) și \(X=\left[\frac{1}{U}\right]\)
- Generăm \(V\sim\mathcal{U}(0,1)\)
- Dacă \(Vcg(X)\leq f(X)\) atunci \(Z=X\) altfel trecem la pasul 1
Pasul 3 se rescrie astfel
\[ Vcg(X)\leq f(X) \iff V\frac{12}{\pi^2}\frac{1}{X(X+1)}\leq \frac{6}{\pi^2 X^2} \]
ceea ce conduce la \(V\leq \frac{1}{2} + \frac{1}{2X}\).
Următoarea funcție implementează metoda respingerii pentru repartiția \(\mathrm{Zipf}(2)\):
gen_Zipf <- function(n){
x <- rep(0, n)
m <- 0
# constanta
c1 <- 12/pi^2
iter <- 0
while(m <= n){
# nr iteratii
iter <- iter + 1
# gen Y din g = 1/k(k+1)
y <- floor(1/runif(1))
# gen V unif [0,1]
v <- runif(1)
# verificam conditia
if (v <= 0.5+1/(2*y)){
m <- m+1
x[m] <- y
}
}
return(list(x = x,
nr_iter = iter,
nr_med = n*c1))
}Putem compara repartiția empirică cu cea teoretică:
Metode particulare de generare
Metodele prezentate în această secțiune se bazează pe transformări de variabile aleatoare.
Repartiția Poisson
În această secțiune vom prezenta o modalitate de generare a observațiilor din repartiția Poisson de parametru \(\lambda\) diferită de cea din Exercițiul 4 bazată pe metoda inversă.
Exercițiul 20 (Repartiția Poisson) Fie \((E_n)_{n\geq 1}\) un șir de variabile aleatoare independente și repartizate \(\mathcal{E}(\lambda)\).
- Pentru \(n\geq 1\) definim
\[ f_n(x) = e^{-\lambda x}\frac{\lambda^n x^{n-1}}{(n - 1)!}\mathbf{1}_{\{x\geq 0\}}, \quad x\in\mathbb{R.} \]
Arătați că \(f_n\) este o densitate de repartiție pentru orice \(n\geq 1\). Repartiția a cărei densitate este \(f_n\) se numește repartiția Gamma de parametrii \(n\geq 1\) și \(\lambda\) și se notează cu \(\Gamma(n, \lambda)\).
Fie \(S_n = \sum_{i=1}^{n}E_i\) pentru \(n\geq 1\). Arătați că \(S_n\) este repartizată \(\Gamma(n, \lambda)\).
Considerăm variabila aleatoare
\[ N = \max\{n\geq 1\,|\,S_n\leq 1\} \]
cu convenția \(N = 0\) dacă \(X_1>1\). Arătați că variabila aleatoare \(N\) este repartizată \(Pois(\lambda)\).
Soluție. Avem:
- Prin inducție vom verifica că \(f_n\) este o densitate de repartiție. Să observăm că \(f_n\geq 0\) prin urmare este suficient să arătăm că \(\int_{\mathbb{R}}f_n(x)\,dx = 1\).
Pentru \(n = 1\) avem
\[ \int_{\mathbb{R}}f_1(x)\,dx = \int_{0}^{\infty}\lambda e^{-\lambda x}\,dx = 1. \]
Presupunem proprietatea adevărată pentru \(n\) și arătăm pentru \(n+1\):
\[ \int_{\mathbb{R}}f_{n+1}(x)\,dx = \left[-\frac{\lambda^n x^n}{n!}e^{-\lambda x}\right]_{0}^{\infty} + \int_{0}^{\infty}n\lambda^n\frac{x^{n-1}}{n!}e^{-\lambda x}\,dx = \int_{\mathbb{R}}f_{n}(x)\,dx = 1. \]
- Pentru a determina repartiția lui \(S_n\) vom folosi noțiunea de funcție generatoare de moment4, i.e. \(M_E(t) = \mathbb{E}[e^{tE}]\).
Se poate calcula cu ușurință că
\[ M_{E_i}(t) = \frac{\lambda}{\lambda-t}, \qquad t<\lambda \]
și cum variabilele aleatoare \(E_1, \ldots, E_n\) sunt independente deducem că funcția generatoare de moment a sumei \(S_n\) este
\[ M_{S_n}(t) = \mathbb{E}[e^{tS_n}] = \prod_{i=1}^{n}M_{E_i}(t) = \left(\frac{\lambda}{\lambda-t}\right)^n, \quad t<\lambda. \]
Știm că dacă \(X\sim \Gamma(n, \lambda)\) atunci \(f_X(x) = \frac{\lambda^{n}}{(n-1)!}x^{n-1} e^{-\lambda x}\) iar funcția generatoare de moment este
\[ M_{X}(t) = \left(\frac{\lambda}{\lambda-t}\right)^n, \quad t<\lambda. \]
Cum cele două funcții generatoare de moment sunt egale și ținând cont de faptul că funcția generatoare caracterizează repartiția, deducem că \(S_n\sim \Gamma(n, \lambda)\).
- Pentru a demonstra că \(N\sim Pois(\lambda)\) este suficient să calculăm \(\mathbb{P}(N = n)\). Avem
\[ \mathbb{P}(N = n) = \mathbb{P}\left(S_n\leq 1<S_{n+1}\right) = \int_{0}^{1}\mathbb{P}(E_{n+1}\geq 1-u\,|\,S_n = u)f_{S_n}(u)\, du, \]
unde \(f_{S_n}\) este densitatea lui \(S_n\) de la punctul a). Ținând seama că \(E_{n+1}\) și \(S_n\) sunt independente și cum \(\mathbb{P}(E_{n+1}\geq 1-u) = e^{-\lambda (1-u)}\) avem că
\[ \begin{aligned} \mathbb{P}(N = n) &= \int_{0}^{1}\mathbb{P}(E_{n+1}\geq 1-u\,|\,S_n = u)f_{S_n}(u)\, du \\ &= \int_{0}^{1}e^{-\lambda (1-u)}\frac{\lambda^{n}}{(n-1)!}x^{n-1} e^{-\lambda x}\,du\\ &= \frac{e^{-\lambda}\lambda^n}{(n-1)!}\int_{0}^{1} u^{n-1}\,du = \frac{e^{-\lambda}\lambda^n}{n!}. \end{aligned} \]
Următoarea funcție permite generarea de observații din repartiția \(\mathrm{Pois}(\lambda)\) din exercițiu:
sim_discrete_pois2 <- function(n, lambda){
# genereaza N obs dintr-o repartitie Poisson de parametru lambda
x <- numeric(n)
for (i in 1:n){
x[i] <- 0
s <- sim_cont_exp(1, lambda)
while(s<=1){
s <- s + sim_cont_exp(1, lambda)
x[i] <- x[i] + 1
}
}
return(x)
}Alternativ, ținând cont de Exercițiul 6, avem:
\[ \begin{aligned} N &= \max\left\{n\geq 1\,|\,\sum_{i=1}^{n}E_i\leq 1\right\}\\ &= \max\left\{n\geq 1\,|\,\sum_{i=1}^{n}-\frac{1}{\lambda}\log(U_i)\leq 1\right\}\\ &= \max\left\{n\geq 1\,|\,\sum_{i=1}^{n}\log(U_i)\geq -\lambda\right\}\\ &= \max\left\{n\geq 1\,|\,\prod_{i=1}^{n}U_i\geq e^{-\lambda}\right\}\\ &= \min\left\{n\geq 1\,|\,\prod_{i=1}^{n}U_i< e^{-\lambda}\right\} - 1 \end{aligned} \]
de unde reiese următoarea funcție
sim_discrete_pois3 <- function(n, lambda){
# genereaza n obs dintr-o repartitie Poisson de parametru lambda
y <- rep(0, n)
for (i in 1:n){
u <- runif(1)
a <- exp(-lambda)
k <- 0
while(u >= a){
u <- u*runif(1)
k <- k+1
}
y[i] <- k
}
return(y)
}Pentru a testa metoda propusă vom vizualiza repartiția simulată în comparație cu cea teoretică:
lambda <- 5
N <- 10000
X <- sim_discrete_pois2(N, lambda)
pX <- table(X)/N
indX <- sort(unique(X))
pT <- dpois(indX, lambda)
dat <- data.frame(x = rep(indX, 2) , y = c(pX, pT),
type = rep(c("Simulat", "Teoretic"),
each = length(pX)))
barplot(rbind(pX, pT),
beside = T,
col = c(myblue, myred),
names.arg = indX,
cex.axis = 0.7,
legend.text = c("Simulat", "Teoretic"),
args.legend = list(bty = "n"))Aceste funcții ar putea fi costisitoare în ceea ce privește timpul de execuție (R nu este foarte eficient atunci când avem bucle imbricate). Următorul cod optimizează procedura:
sim_discrete_pois4 <- function(n, lambda = 1){
x <- sim_cont_exp(n, lambda)
i <- 0
l <- which(x<=1)
# realizari cu valoarea 0
out <- rep(0, sum(x > 1))
while(length(l) > 0){
i <- i + 1
x <- x[l] + sim_cont_exp(length(l), lambda)
l <- which(x<=1)
# realizari cu valoarea i
out <- c(out, rep(i, sum(x > 1)))
}
return(out)
}Pentru a compara cele patru funcții considerăm următorul tabel:
| functia | timp |
|---|---|
| sim_discrete_pois1 | 0.08 |
| sim_discrete_pois2 | 0.22 |
| sim_discrete_pois3 | 0.11 |
| sim_discrete_pois4 | 0.02 |
Repartiția \(\chi^2\)
În această subsecțiune vom prezenta o metodă de generare a observațiilor din repartiția \(\chi^2(k)\). Să reamintim că o variabilă aleatoare \(X\sim\chi^2(k)\) dacă admite ca densitate pe
\[ f(x) = \frac{1}{2^{k / 2} \Gamma\left(\frac{k}{2}\right)} x^{k / 2-1} e^{-x / 2} \mathbf{1}_{\{x>0\}}. \]
Exercițiul 21 (Repartiția \(\chi^2(k)\)) Plecând de la rezultatul de caracterizare a repartiției \(X\sim\chi^2(k)\): dacă \(X_1,\ldots,X_k\) sunt variabile aleatoare i.i.d. repartizate \(\mathcal{N}(0, 1)\) atunci variabila aleatoare \(X = \sum_{i = 1}^{k}X_i^2\) este repartizată \(\chi^2(k)\), propuneți o metodă de simulare din repartiția \(\chi^2(k)\) și descrieți algoritmul.
Soluție. Observăm că pentru a genera o observație dintr-o repartiție \(\chi^2(k)\) trebuie să generăm \(k\) observații normale independente și să adunăm pătratele lor. Avem următoarea funcție care implementează acest rezultat de caracterizare:
sim_cont_chisq1 <- function(n, k = 1){
# n - nr de obs
# k - grade de libertate
x <- matrix(rnorm(n*k, mean = 0, sd = 1), ncol = k)
out <- rowSums(x^2)
return(out)
}Pentru a verifica algoritmul generăm un eșantion de volum \(1000\) din repartiția \(\chi^2(5)\), trasăm histograma acestuia și suprapune densitatea teoretică peste aceasta:
Trebuie remarcat că această metodă poate să nu fie optimă din punct de vedere al costului de memorie, în special pentru \(n\) și \(k\) mare. Pentru a evita această problemă putem să apelăm la o buclă for:
sim_cont_chisq2 <- function(n, k = 1){
# n - nr de obs
# k - grade de libertate
out <- numeric(n)
for (i in 1:n){
out[i] <- sum(rnorm(k, mean = 0, sd = 1)^2)
}
return(out)
}Cu toate acestea, ambele metode folosesc \(k\) observații normale pentru generarea unei observații \(\chi^2(k)\) ceea ce poate conduce la un algoritm neeficient din punct de vedere computațional. Dacă ținem cont că repartiția \(\mathrm{Exp}\left(\frac{1}{2}\right)\) este echivalentă cu repartiția \(\chi^2(2)\) (se pot compara densitățile de repartiție) atunci putem propune o metodă de simulare alternativă: atunci când \(k\) este par putem genera \(\frac{k}{2}\) observații \(\mathrm{Exp}\left(\frac{1}{2}\right)\) independente iar când \(k\) este impar, generăm \(\left\lfloor\frac{k}{2} \right\rfloor\) observații \(\mathrm{Exp}\left(\frac{1}{2}\right)\) independente și o observație repartizată \(\mathcal{N}(0,1)\). Algoritmul este descris de funcția de mai jos:
sim_cont_chisq3 <- function(n, k = 1){
# n - nr de obs
# k - grade de libertate
k1 <- floor(k/2)
x <- matrix(rexp(n*k1, rate = 0.5), ncol = k1)
out <- rowSums(x)
if (2*k1 != k){
out <- out + rnorm(n, 0, 1)^2
}
return(out)
}Pentru a vedea care algoritm este mai eficient, considerăm timpul de execuție al celor trei funcții pentru \(n = 100000\) de observații și \(k = 15\):
| functia | timp |
|---|---|
| sim_cont_chisq1 | 0.06 |
| sim_cont_chisq2 | 0.18 |
| sim_cont_chisq3 | 0.01 |
Să nu uităm că în R putem să generăm \(n\) observații din repartiția \(\chi^2(k)\) folosind funcția rchisq(n, df = k).
Repartiția t-Student
În această subsecțiune vom prezenta o metodă de generare a observațiilor din repartiția Student cu \(k\) grade de libertate, \(t_k\). Să reamintim că o variabilă aleatoare \(X\sim t_k\) dacă admite ca densitate pe
\[ f(x) = \frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{\pi n}\Gamma\left(\frac{n}{2}\right)}\left(1+\frac{x^{2}}{n}\right)^{-\frac{n+1}{2}},\, x \in \mathbb{R}. \]
Din rezultatul de caracterizare a repartiție Student am văzut că dacă \(U\) este o variabilă aleatoare repartizată \(\mathcal{N}(0, 1)\) și \(V\) o variabilă repartizată \(\chi^2(k)\), cu \(U\) și \(V\) independente, atunci variabila aleatoare \(T = \frac{U}{\sqrt{\frac{V}{k}}}\) este repartizată Student cu \(k\) grade de libertate.
Exercițiul 22 (Repartiția \(t_k\)) Plecând de la rezultatul de caracterizare a repartiției \(t_k\), propuneți o metodă de simulare din repartiția Student și descrieți algoritmul.
Soluție. Observăm că pentru a genera o observație dintr-o repartiție \(t_k\) trebuie să generăm o observație normală standard și o observație \(\chi^2(k)\). Avem următoarea funcție care implementează acest rezultat de caracterizare:
sim_cont_t <- function(n, k = 1){
# n - nr de obs
# k - grade de libertate
u <- rnorm(n, 0, 1)
v <- rchisq(n, df = k)
out <- u/sqrt(v/k)
return(out)
}În funcția de mai sus am putea să folosim funcțiile pe care le-am creat pentru generarea observațiilor normale (e.g. sim_cont_normal1 în ?@exr-stat-sim-met-part-norm-e1) și respectiv \(\chi^2(k)\) (e.g. sim_cont_chisq3 în Exercițiul 21).
Pentru a verifica algoritmul generăm un eșantion de volum \(1000\) din repartiția \(t_5\), trasăm histograma acestuia și suprapune densitatea teoretică peste aceasta:
Trebuie remarcat că în R putem să generăm \(n\) observații din repartiția \(t_(k)\) folosind funcția rt(n, df = k).
Repartiția Fisher-Snedecor
În această subsecțiune vom prezenta o metodă de generare a observațiilor din repartiția Fisher-Snedecor cu \(n_1\) grade de libertate la numărător și \(n_2\) grade de libertate la numitor, \(F_{n_1,n_2}\). Să reamintim că o variabilă aleatoare \(X\sim F_{n_1,n_2}\) dacă admite ca densitate pe
\[ f_{n_{1}, n_{2}}(x)=\frac{\Gamma\left(\frac{n_{1}+n_{2}}{2}\right)}{\Gamma\left(\frac{n_{1}}{2}\right) \Gamma\left(\frac{n_{2}}{2}\right)}\left(\frac{n_{1}}{n_{2}}\right)^{\frac{n_{1}}{2}} \frac{x^{\frac{n_{1}-2}{2}}}{\left(1+\frac{n_{1}}{n_{2}} x\right)^{\frac{n_{1}+n_{2}}{2}}} \quad \text { dacă } x>0 \quad(0 \text { altfel}). \]
Din rezultatul de caracterizare a repartiție Fisher-Snedecor am văzut că dacă \(U\) o variabilă aleatoare repartizată \(\chi^2_{n_1}\) și \(V\) o variabilă aleatoare repartizată \(\chi^2_{n_2}\), cu \(U\) și \(V\) independente, atunci variabila aleatoare \(F = \frac{U/n_1}{V/n_2}\) este repartizată Fisher-Snedecor \(F_{n_1,n_2}\).
Exercițiul 23 (Repartiția \(F_{n_1,n_2}\)) Plecând de la rezultatul de caracterizare a repartiției \(F_{n_1,n_2}\), propuneți o metodă de simulare din repartiția Fisher-Snedecor și descrieți algoritmul.
Soluție. Pentru a genera o observație dintr-o repartiție \(F_{n_1,n_2}\) trebuie să generăm o observație \(\chi^2(n_1)\) și o observație \(\chi^2(n_2)\) independente. Avem următoarea funcție care implementează acest rezultat de caracterizare:
sim_cont_f <- function(n, df1 = 1, df2 = 1){
# n - nr de obs
# df1 - grade de libertate numarator
# df2 - grade de libertate numitor
u <- rchisq(n, df = df1)
v <- rchisq(n, df = df2)
out <- (u/df1)/(v/df2)
return(out)
}În funcția de mai sus am putea să folosim funcțiile pe care le-am creat pentru generarea observațiilor \(\chi^2(k)\) (e.g. sim_cont_chisq3 în Exercițiul 21).
Pentru a verifica algoritmul generăm un eșantion de volum \(1000\) din repartiția \(F_{5,10}\), trasăm histograma acestuia și suprapune densitatea teoretică peste aceasta:
Trebuie remarcat că în R putem să generăm \(n\) observații din repartiția \(F(n_1, n_2)\) folosind funcția rf(n, df1 = $n_1$, df2 = $n_2$).
Repartiția Beta
În această subsecțiune vom prezenta o metodă de generare a observațiilor din repartiția Beta \(B(\alpha,\beta)\).
Exercițiul 24 (Repartiția \(B(\alpha,\beta)\)) Fie \(X\) și \(Y\) două variabile aleatoare independente repartizate \(\Gamma(\alpha, a)\) și respectiv \(\Gamma(\beta, a)\). Arătați că \(\frac{X}{X+Y}\sim B(\alpha,\beta)\). Propuneți o metodă de simulare din repartiția \(B(\alpha,\beta)\) și descrieți algoritmul.
Soluție. Să reamintim că \(X\sim\Gamma(\alpha, a)\) dacă admite densitatea de repartiție
\[ f_X(x) = \frac{a^{\alpha}}{\Gamma(\alpha)} x^{\alpha-1} e^{-a x},\quad \forall x>0 \]
iar \(Z\sim B(\alpha,\beta)\) dacă admite densitatea de repartiție
\[ f_Z(z) = \frac{1}{B(\alpha, \beta)} x^{\alpha-1} (1-x)^{\beta-1},\quad 0\leq x\leq 1, \]
unde \(B(\alpha, \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)} = \int_{0}^{1}x^{\alpha-1} (1-x)^{\beta-1}\,dx\).
Pentru început vom determina densitatea comună a vectorului \((U_1,U_2) = \left(X + Y, \frac{X}{X+Y}\right)\) și, plecând de la aceasta, vom găsi repartiția marginală a lui \(U_2\). Considerăm transformarea \(g: A\to B\) definită prin
\[ g:(x, y) \mapsto(u_1, u_2)=\left(x+y, \frac{x}{x+y}\right) \]
astfel că \((U_1,U_2) = g(X, Y)\). Se observă că suportul lui \((X,Y)\) este \(A = \{(x,y)\,|\, x>0,y>0\}\) iar suportul lui \((U_1,U_2)\) este \(B = \{(u_1,u_2)\,|\, u_1>0,0<u_2<1\}\) și în plus funcția \(g\) este bijectivă (surjectivitatea este garantată iar injectivitatea se poate verifica ușor) iar inversa sa este dată de
\[ g^{-1}:(u_1, u_2) \mapsto\left(u_1 u_2, u_1(1 - u_2)\right). \]
Matricea Jacobiană corespunzătoare lui \(g^{-1}\) este
\[ J_{g^{-1}}=\left(\begin{array}{cc} u_2 & u_1 \\ 1-u_2 & -u_1 \end{array}\right) \]
de unde găsim determinantul \(\operatorname{det}\left(J_{g^{-1}}(u_1, u_2)\right)=-u_1\).
Ținând cont de faptul că \(X\) și \(Y\) sunt independente rezultă că densitatea comună a vectorului \((X,Y)\) este
\[ \begin{aligned} f_{X,Y}(x,y) &= f_X(x) f_Y(y)=\left(\frac{a^{\alpha}}{\Gamma(\alpha)} x^{\alpha-1} e^{-a x}\right) \left(\frac{a^{\beta}}{\Gamma(\beta)} y^{\beta-1} e^{-a y}\right)\\ & = \frac{a^{\alpha + \beta}}{\Gamma(\alpha)\Gamma(\beta)} x^{\alpha-1} y^{\beta-1} e^{-a (x + y)} \end{aligned} \]
prin urmare densitatea comună a vectorului \((U_1,U_2)\) este
\[ \begin{aligned} f_{U_1,U_2}(u_1, u_2) & =f_{U_1,U_2}\left(g^{-1}(u_1, u_2)\right)\left|\operatorname{det}\left(J_{g-1}(u_1, u_2)\right)\right|=f_{U_1,U_2}\left(u_1 u_2, u_1(1-u_2)\right) |-u_1|\\ & = \frac{a^{\alpha+\beta}}{\Gamma(\alpha)\Gamma(\beta)}(u_1 u_2)^{\alpha -1}\left[u_1(1-u_2)\right]^{\beta - 1}e^{-a\left[u_1 u_2 + u_1(1-u_2)\right]} u_1\\ & = \frac{a^{\alpha+\beta}}{\Gamma(\alpha)\Gamma(\beta)}u_1^{\alpha + \beta -1}u_2^{\alpha -1}\left(1-u_2\right)^{\beta - 1}e^{-a u_1}. \end{aligned} \]
Densitatea marginală a lui \(U_2\) este
\[ \begin{aligned} f_{U_2}\left(u_2\right) & \stackrel{0<u_2<1}{=} \int_{u_1=0}^{\infty} \frac{a^{\alpha+\beta}}{\Gamma(\alpha) \Gamma(\beta)} u_1^{\alpha+\beta-1} u_2^{\alpha-1}\left(1-u_2\right)^{\beta-1} e^{-a u_1} d u_1 \\ & =\frac{a^{\alpha+\beta}}{\Gamma(\alpha) \Gamma(\beta)} u_2^{\alpha-1}\left(1-u_2\right)^{\beta-1} \int_{0}^{\infty} u_1^{\alpha+\beta-1} e^{-a u_1} d u_1 \\ & = \frac{a^{\alpha+\beta}}{\Gamma(\alpha) \Gamma(\beta)} u_2^{\alpha-1}\left(1-u_2\right)^{\beta-1} \int_{0}^{\infty} \left(\frac{t}{a}\right)^{\alpha+\beta-1} e^{-t} \frac{1}{a}d t\\ & =\frac{1}{\Gamma(\alpha) \Gamma(\beta)} u_2^{\alpha-1}\left(1-u_2\right)^{\beta-1} \times \Gamma(\alpha+\beta)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} u_2^{\alpha-1}\left(1-u_2\right)^{\beta-1}. \end{aligned} \]
Sumarizând, am găsit că
\[ f_{U_2}\left(u_2\right)=\left\{\begin{array}{cc} \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} u_2^{\alpha-1}\left(1-u_2\right)^{\beta-1}, & 0<u_2<1 \\ 0, & \text { altfel. } \end{array}\right. \]
ceea ce arată că \(U_2 = \frac{X}{X+Y}\sim B(\alpha, \beta)\).
Pentru densitatea marginală a lui \(U_1\) găsim că
\[ \begin{aligned} f_{U_1}\left(u_1\right) & \stackrel{u_1>0}{=} \int_{u_2=0}^1 \frac{a^{\alpha+\beta}}{\Gamma(\alpha) \Gamma(\beta)} u_1^{\alpha+\beta-1} u_2^{\alpha-1}\left(1-u_2\right)^{\beta-1} e^{-a u_1} d u_2 \\ & =\frac{a^{\alpha+\beta}}{\Gamma(\alpha) \Gamma(\beta)} u_1^{\alpha+\beta-1} e^{-a u_1} \int_{0}^1 u_2^{\alpha-1}\left(1-u_2\right)^{\beta-1} d u_2 \\ & =\frac{a^{\alpha+\beta}}{\Gamma(\alpha) \Gamma(\beta)} u_1^{\alpha+\beta-1} e^{-a u_1} \times \frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha+\beta)}=\frac{a^{\alpha+\beta}}{\Gamma(\alpha+\beta)} u_1^{\alpha+\beta-1} e^{-a u_1} \end{aligned} \]
Astfel, densitate lui \(U_1 = X + Y\) este
\[ f_{U_1}\left(u_1\right)=\left\{\begin{array}{cc} \frac{1}{\Gamma(\alpha+\beta)} u_1^{\alpha+\beta-1} e^{-u_1}, & u_1>0 \\ 0, & \text { altfel } \end{array}\right. \]
densitate care coincide cu densitatea variabilei aleatoare \(\frac{1}{a}\Gamma(\alpha+\beta, 1)\). Mai mult, dacă ne uităm la densitatea comună a vectorului \((U_1, U_2)\) deducem că
\[ \begin{aligned} f_{U_1, U_2}\left(u_1, u_2\right) & =\frac{a^{\alpha+\beta}}{\Gamma(\alpha) \Gamma(\beta)} u_1^{\alpha+\beta-1} u_2^{\alpha-1}\left(1-u_2\right)^{\beta-1} e^{-a u_1} \\ & =\underbrace{\frac{a^{\alpha+\beta}}{\Gamma(\alpha+\beta)} u_1^{\alpha+\beta-1} e^{-a u_1}}_{f_{U_1}\left(u_1\right)} \times \underbrace{\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} u_2^{\alpha-1}\left(1-u_2\right)^{\beta-1}}_{f_{U_2}\left(u_2\right)}\\ &=f_{U_1}\left(u_1\right) f_{U_2}\left(u_2\right) \end{aligned} \]
ceea ce arată că \(U_1\sim \frac{1}{a}\Gamma(\alpha+\beta, 1)\) și \(U_2\sim B(\alpha, \beta)\) sunt independente.
Următoarea funcție implementează acest algoritm:
sim_cont_beta <- function(n, alpha = 1, beta = 1){
# n - nr de obs
# alpha - parametrul alpha
# beta - parametrul beta
x <- rgamma(n, shape = alpha, rate = 1)
y <- rgamma(n, shape = beta, rate = 1)
out <- x / (x + y)
return(out)
}Pentru a verifica algoritmul generăm un eșantion de volum \(1000\) din repartiția Beta \(B(2, 3)\), trasăm histograma acestuia și suprapune densitatea teoretică peste aceasta:
Trebuie remarcat că în R putem să generăm \(n\) observații din repartiția Beta \(B(\alpha,\beta)\) folosind funcția rbeta(n, shape1 =\(\alpha\), shape2 =\(\beta\)).
Repartiția Cauchy
În această subsecțiune vom prezenta o metodă alternativă de generare a observațiilor din repartiția Cauchy \(C(\alpha,\beta)\). O primă metodă a fost dată în Secțiunea 0.3.2.4 și s-a bazat pe metoda inversă.
Exercițiul 25 (Repartiția Cauchy) Fie \(X\) și \(Y\) două variabile aleatoare independente repartizate \(\mathcal{N}(0,1)\). Arătați că \(\frac{X}{Y}\sim C(0,1)\).
Soluție. Metoda propusă în acest exercițiu este o metodă alternativă la metoda bazată directă descrisă în Exercițiul 9. Vom determina pentru început repartiția comună a vectorului \((U_1, U_2) = \left(\frac{X}{Y}, Y\right)\) și, plecând de la aceasta, vom găsi repartiția marginală a lui \(U_1\). În acest sens considerăm transformarea \(g:\mathbb{R}\times \mathbb{R}\setminus \{0\} \mapsto \mathbb{R}\times \mathbb{R}\setminus \{0\}\) definită prin
\[ g:(x, y) \mapsto(u_1, u_2)=\left(\frac{x}{y}, y\right) \]
astfel că \((U_1, U_2) = g(X, Y)\) și a cărei inversă este dată de
\[ g^{-1}:(u_1, u_2) \mapsto\left(u_1 u_2, u_2\right). \]
Matricea Jacobiană corespunzătoare lui \(g^{-1}\) este
\[ J_{g^{-1}}=\left(\begin{array}{cc} u_2 & u_1\\ 0 & 1 \end{array}\right) \]
de unde găsim determinantul \(\operatorname{det}\left(J_{g^{-1}}(u_1, u_2)\right)=u_2\).
Cum \(X\) și \(Y\) sunt variabile aleatoare independente rezultă că densitatea comună a vectorului \((X, Y)\) este
\[ f_{X, Y}(x, y)=f_X(x) f_Y(y)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\frac{1}{\sqrt{2\pi}}e^{-\frac{y^2}{2}}. \]
Găsim astfel că densitatea comună a vectorului \((U_1,U_2)\) este
\[ \begin{aligned} f_{U_1,U_2}(u_1, u_2) & =f_{U_1,U_2}\left(g^{-1}(u_1, u_2)\right)\left|\operatorname{det}\left(J_{g-1}(u_1, u_2)\right)\right|=f_{U_1,U_2}\left(u_1 u_2, u_2\right) |u_2|\\ & = \frac{1}{\sqrt{2\pi}}e^{-\frac{(u_1 u_2)^2}{2}}\frac{1}{\sqrt{2\pi}}e^{-\frac{u_2^2}{2}}|u_2|\\ & = \frac{1}{2\pi}e^{-\frac{u_1^2 u_2^2 + u_2^2}{2}}|u_2|. \end{aligned} \]
iar densitatea marginală a lui \(U_1\) este
\[ \begin{aligned} f_{U_1}\left(u_1\right) & = \int_{-\infty}^{\infty} \frac{1}{2\pi}e^{-\frac{u_1^2 u_2^2 + u_2^2}{2}}|u_2| d u_2 \\ & =\frac{1}{\pi}\int_{0}^{\infty} e^{-\frac{u_2^2 (u_1^2 + 1)}{2}}u_2 d u_2 \end{aligned} \]
Considerând schimbarea de variabilă \(t = \frac{u_2^2 (u_1^2 + 1)}{2}\) găsim \(u_2^2 = \frac{2t}{u_1^2+1}\) de unde \(2u_2 d u_2 = \frac{2}{u_1^2+1} d t\) sau \(u_2 d u_2 = \frac{1}{u_1^2+1} d t\) cu \(t\geq 0\) ceea ce conduce la
\[ \begin{aligned} f_{U_1}\left(u_1\right) & = \frac{1}{\pi}\int_{0}^{\infty} e^{-t} \frac{1}{u_1^2+1} d t = \frac{1}{\pi}\frac{1}{u_1^2+1} \underbrace{\int_{0}^{\infty} e^{-t} d t}_{=1}\\ & = \frac{1}{\pi}\frac{1}{u_1^2+1}. \end{aligned} \]
Avem următoarea funcție care implementează acest rezultat de caracterizare:
sim_cont_cauchy2 <- function(n = 1, alpha = 0, beta = 1){
# n - nr de obs
# alpha - parametrul de locatie
# beta - parametrul de scala
x <- rnorm(n, 0, 1)
y <- rnorm(n, 0, 1)
out <- alpha + beta * x/y
return(out)
}În funcția de mai sus am putea să folosim funcțiile pe care le-am creat pentru generarea observațiilor \(\mathcal{N}(0,1)\) (e.g. sim_cont_normal1 în ?@exr-stat-sim-met-part-norm-e1).
Pentru a verifica algoritmul generăm un eșantion de volum \(10000\) din repartiția \(C(2, 3)\), trasăm histograma acestuia și suprapune densitatea teoretică peste aceasta:
Trebuie remarcat că în R putem să generăm \(n\) observații din repartiția Cauchy \(C(\alpha,\beta)\) folosind funcția rcauchy(n, location = $\alpha$, scale = $\beta$).
Referințe
Note de subsol
Spunem că un estimator nedeplasat este mai eficient decât un altul dacă varianța lui este mai mică↩︎
Această metodă de a estima e este discutată în lucrarea: Russell, K.G. Estimating the value of \(e\) by simulation, The American Statistician, Vol. 45, Nr. 1, pp 66-68, 1991.↩︎
Pentru mai multe detalii se poate consulta pagina https://en.wikipedia.org/wiki/Wigner_semicircle_distribution.↩︎
Problema se poate face și fără această noțiune, ținând seama de schimbarea de variabilă \(\phi:(x_1,\ldots, x_n)\to(s_1, \ldots, s_n)\) cu \(s_n = \sum_{k=1}^{n}x_k\) a cărei inversă \(\phi^{-1}\) este dată prin \(x_1 = s_1\) și \(x_k = s_k-s_{k-1}\). Determinantul matricii Jacobiene asociate lui \(\phi^{-1}\) este \(1\) iar imaginea \(\phi([0,\infty) = \{0\leq s_1\leq\cdots\leq s_n\}\) ceea ce conduce la rezultatul dorit.↩︎