comparare_estimatori <- function(n, mu, sigma, S){
# Initializam
mu1 <- numeric(S)
mu2 <- numeric(S)
mu3 <- numeric(S)
# repetam experimentul de S ori
for (i in 1:S){
x <- rnorm(n, mean = mu, sd = sigma)
# calculam estimatorii
mu1[i] <- mean(x)
mu2[i] <- median(x)
mu3[i] <- (min(x)+max(x))/2
}
return(list(M = cbind(mu1 = mu1, mu2 = mu2, mu3 = mu3),
vM = cbind(var_mu1 = var(mu1), var_mu2 = var(mu2), var_mu3 = var(mu3))))
}Proprietăți ale estimatorilor
Exemplu de comparare a trei estimatori
Exercițiul 1.1 Fie \(X_1,X_2,\ldots,X_n\) un eșantion de volum \(n\) dintr-o populație normală de medie \(\mu\) și varianță \(\sigma^2\). Atunci
\[ \hat{\mu}_1 = \frac{1}{n}\sum_{i=1}^{n}X_i, \quad \hat{\mu}_2 = M_n\,(\text{mediana}\,), \quad \hat{\mu}_3 = \frac{X_{(1)} + X_{(n)}}{2} \]
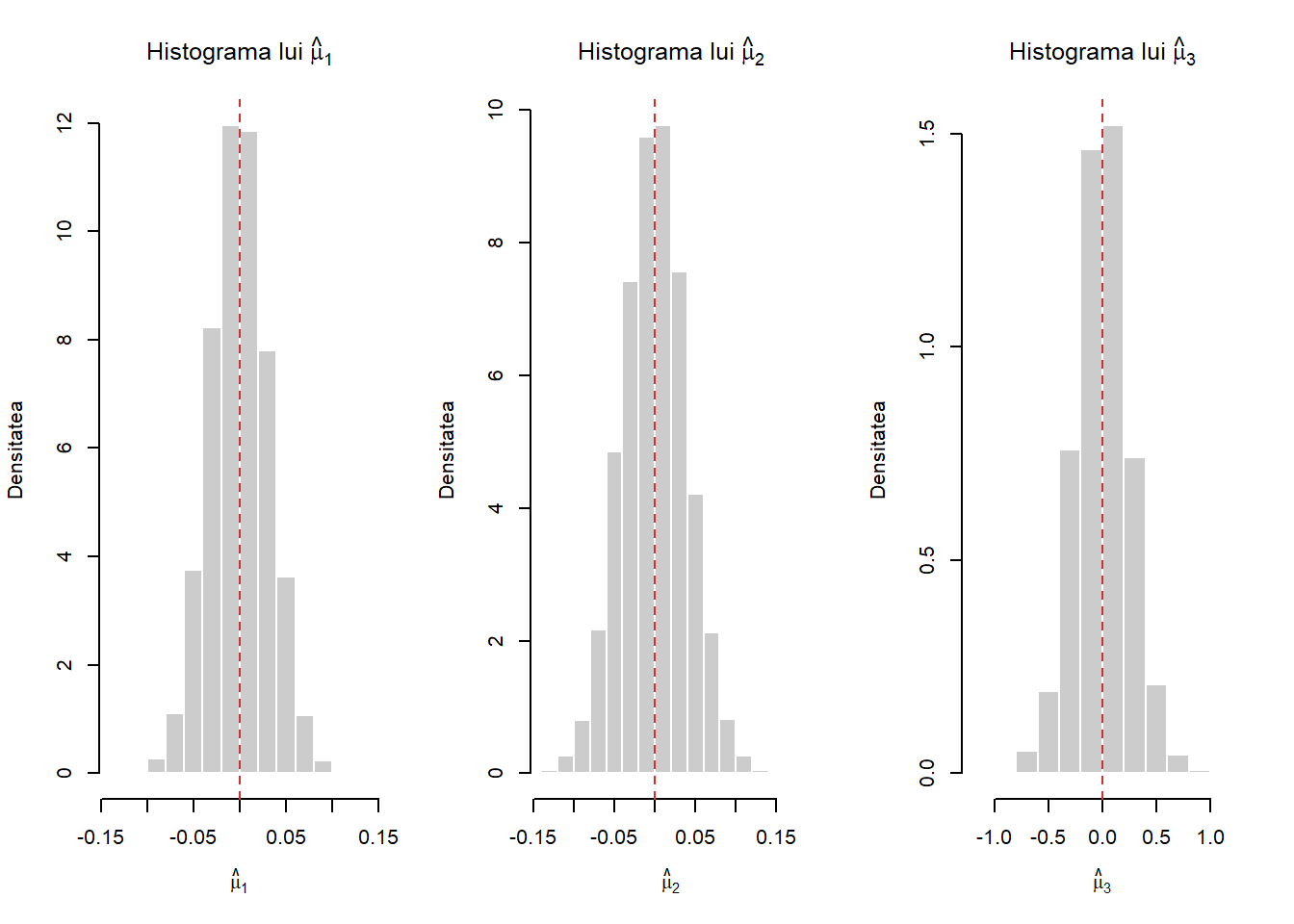
sunt trei estimatori punctuali pentru \(\mu\). Creați o funcție care să ilustreze cum sunt repartizați cei trei estimatori. Începeți cu \(n = 10\), \(\mu = 0\) și \(\sigma^2 = 1\) și trasați histogramele pentru a-i compara. Ce se întâmplă dacă schimbați \(n\), \(\mu\) sau \(\sigma^2\) ?
Soluție. Vom crea o funcție numită comparare_estimatori care va construi repartițiile celor trei estimatori:
Ca exemplu să considerăm \(\mu = 3\) și \(\sigma^2 = 2\):
# Exemplu
mu <- 3
sigma <- 2
n <- 1000
N <- 10000
mu_hat <- comparare_estimatori(n, mu, sigma, N)
# variantele celor trei estimatori
mu_hat$vM var_mu1 var_mu2 var_mu3
[1,] 0.004072323 0.006315998 0.2458911# varianta teoretica a lui \bar{X}_n
sigma^2/n [1] 0.004Pentru a ilustra grafic histogramele celor trei estimatori, considerăm \(\mu = 0\) și \(\sigma^2 = 1\) și avem:
mu <- 0
sigma <- 1
n <- 1000
S <- 10000
a <- comparare_estimatori(n, mu, sigma, S)
par(mfrow = c(1,3))
hist(a$M[,1], freq=FALSE, xlab=expression(hat(mu)[1]),
col="gray80", border="white",
main = expression(paste("Histograma lui ", hat(mu)[1])),
ylab = "Densitatea")
abline(v=mu, col = "brown3", lty = 2)
hist(a$M[,2], freq=FALSE, xlab=expression(hat(mu)[2]),
col="gray80", border="white",
main = expression(paste("Histograma lui ", hat(mu)[2])),
ylab = "Densitatea")
abline(v=mu, col = "brown3", lty = 2)
hist(a$M[,3], freq=FALSE, xlab=expression(hat(mu)[3]),
col="gray80", border="white",
main = expression(paste("Histograma lui ", hat(mu)[3])),
ylab = "Densitatea")
abline(v=mu, col = "brown3", lty = 2)Ilustrarea consistenței unui estimator
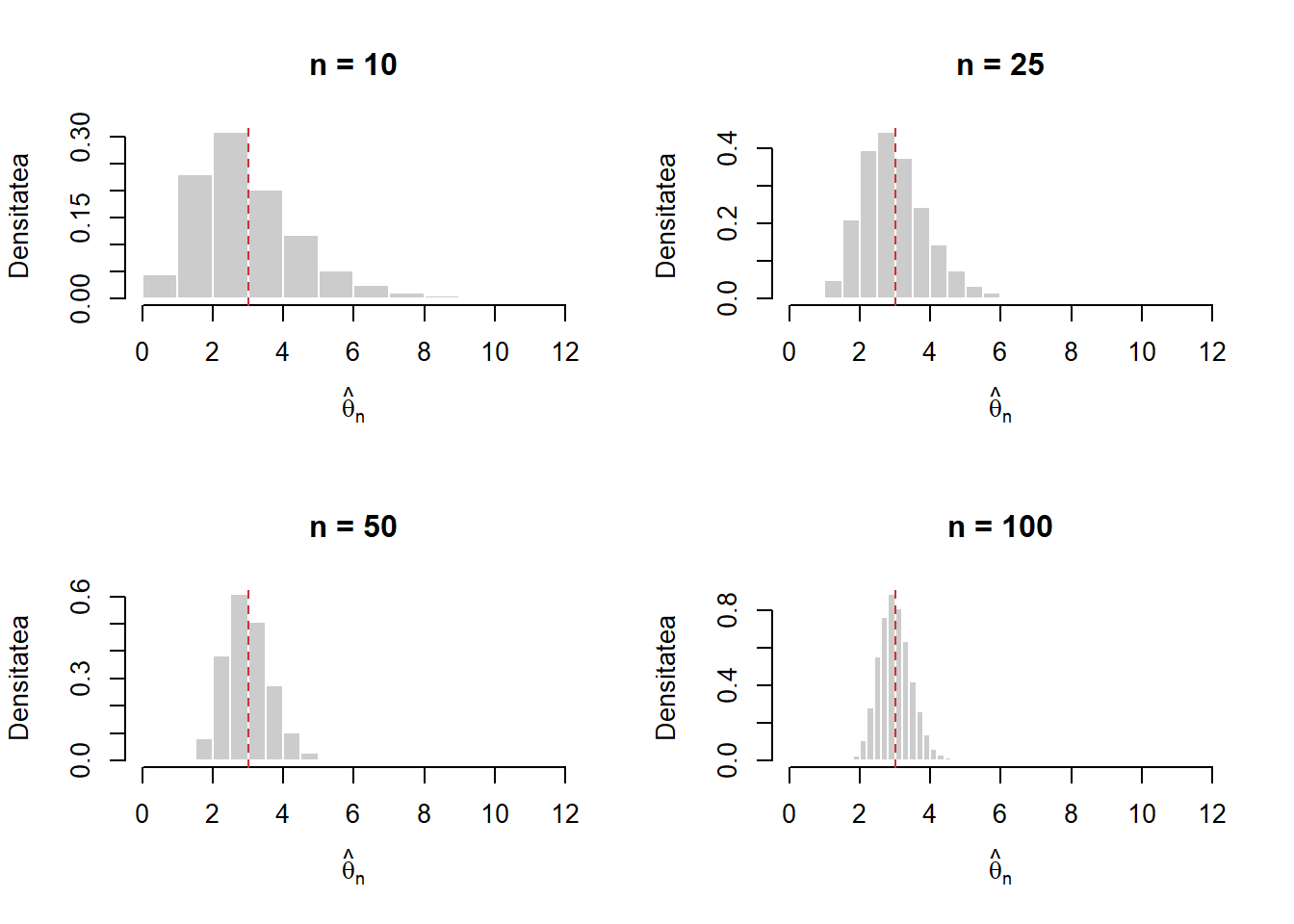
Exercițiul 2.1 Fie \(X_1,X_2,\ldots,X_n\) un eșantion de volum \(n\) dintr-o populație \(Pois(\theta)\). Ilustrați grafic consistența estimatorului \(\hat{\theta}_n = S_n^2\) trasând histograma repartiției lui \(\hat{\theta}_n\) pentru \(n\in\{10,25,50,100\}\). Ce observați?
Soluție. Considerăm funcția pois_est care pentru \(\theta\) fixat simulează repartiția estimatorului \(\hat{\theta}_n\):
pois_est1 <- function(n, theta, S){
# initializare
sigma1 <- numeric(S)
for (i in 1:S){
x <- rpois(n, theta)
sigma1[i] <- var(x)
}
# afisam varianta estimatorului
print(paste0("Pentru n = ", n," varianta estimatorului este ", var(sigma1)))
return(sigma1)
}Considerând \(\theta = 3\) și \(n\in\{10,25,50,100\}\) avem:
theta <- 3
par(mfrow=c(2,2))
vals <- c(10, 25, 50, 100)
for (i in vals){
a <- pois_est1(i, theta, 50000)
hist(a, freq=FALSE,
xlab=expression(hat(theta)[n]),
col="gray80", border="white",
main = paste0("n = ", i), xlim = c(0,12),
ylab = "Densitatea")
abline(v=theta, col = "brown3", lty = 2)
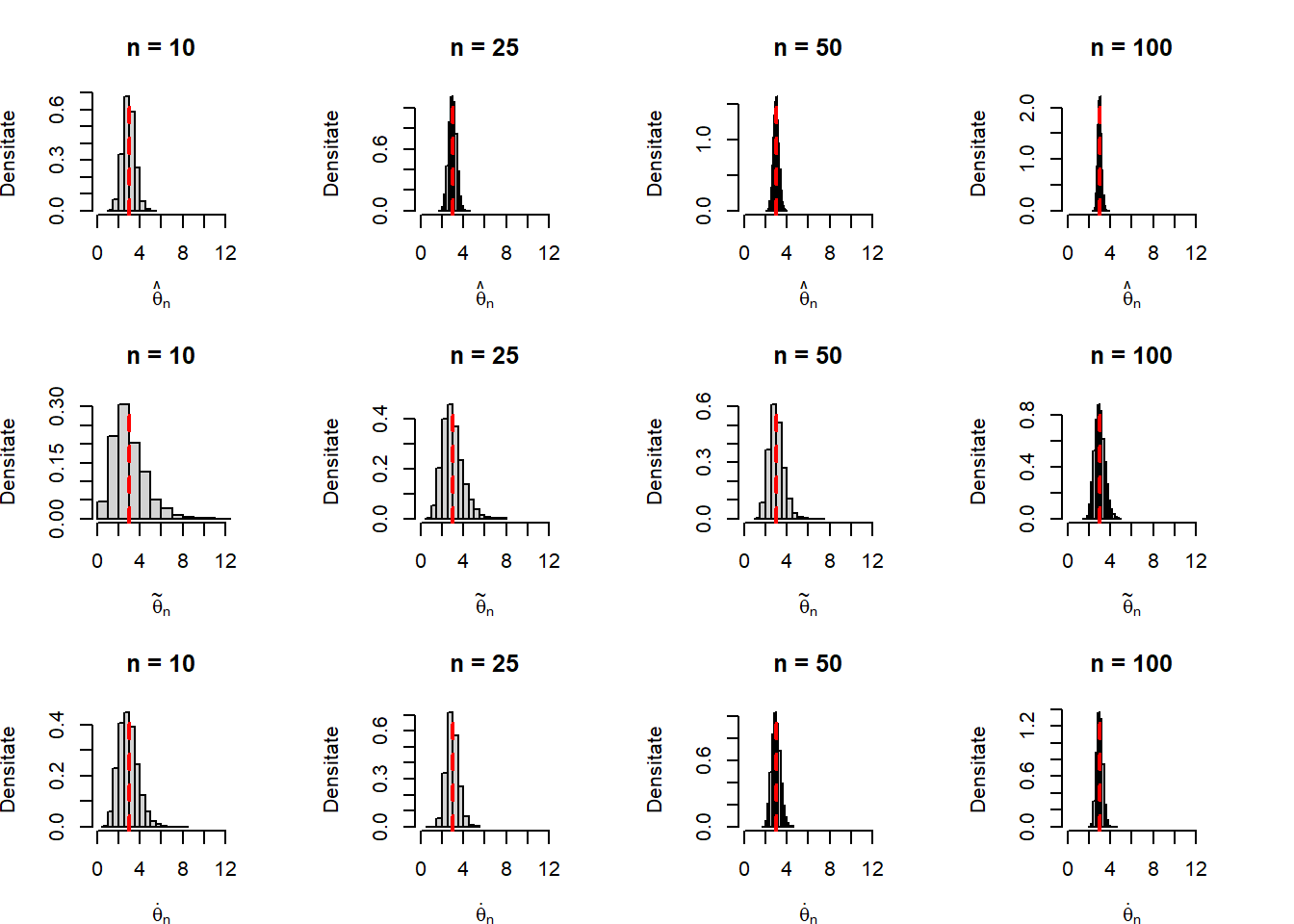
}[1] "Pentru n = 10 varianta estimatorului este 2.28936720674162"[1] "Pentru n = 25 varianta estimatorului este 0.869201285784845"[1] "Pentru n = 50 varianta estimatorului este 0.425499712021584"[1] "Pentru n = 100 varianta estimatorului este 0.211003977718309"Exercițiul 2.2 Ce se întâmplă dacă în loc de \(\hat{\theta}_n\) considerăm estimatorul \(\tilde{\theta}_n = \bar{X}_n\) sau estimatorul \(\dot{\theta}_n = \sqrt{\bar{X}_n S_n^2}\) ?
Soluție. Considerăm acum funcția est_Poisson care va simula repartițiile celor trei estimatori și varianțele acestora:
est_Poisson <- function(n = 10, theta = 1, N = 1000){
e <- matrix(0, nrow = N, ncol = 3)
for (i in 1:N){
x <- rpois(n, theta)
e[i, 1] <- mean(x)
e[i, 2] <- var(x)
e[i, 3] <- sqrt(e[i, 1] * e[i, 2])
}
return(list(e_Pois = e,
v_Pois = c(var(e[, 1]), var(e[, 2]), var(e[, 3]))))
}Ilustrăm grafic repartițiile de eșantionare pentru cei trei estimatori considerând \(\theta = 3\) și \(n\in\{10,25,50,100\}\) și observăm cum acestea se concentrează în jurul parametrului \(\theta\) pe care îl estimează:
theta <- 3
n <- c(10, 25, 50, 100)
N <- 10000
par(mfrow = c(3, length(n)))
par(mai=c(0.5,0.5,0.5,0.5), bty = "n")
# par(fig = c(0, 1, 0, 0.45))
titles <- c("hat(theta)[n]",
"tilde(theta)[n]",
"dot(theta)[n]")
for (i in 1:3){
for (j in 1:length(n)){
e_hat <- est_Poisson(n[j], theta, N)$e_Pois
hist(e_hat[, i], probability = TRUE,
main = paste("n =", n[j]),
xlab = str2lang(titles[i]),
ylab = "Densitate",
xlim = c(0, 12))
abline(v = theta,
col = "red",
lwd = 2,
lty = 2)
}
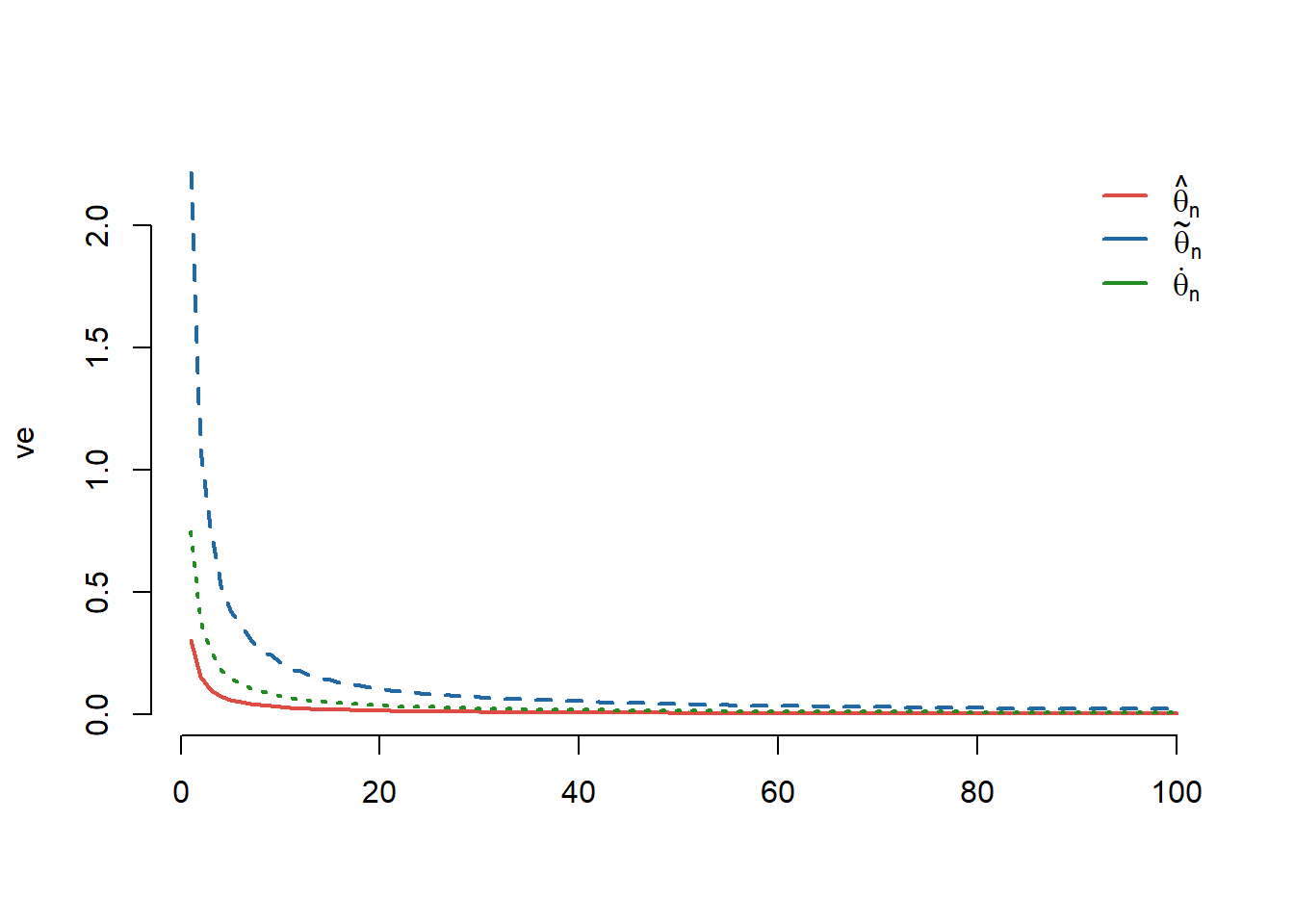
}Observăm în figura de mai jos convergența varianțelor celor trei estimatori către \(0\):
# variantele se duc la 0
n <- seq(10, 1000, 10)
ve <- matrix(0, nrow = length(n), ncol = 3)
for(i in 1:length(n)){
ve[i, ] <- est_Poisson(n[i], theta, N)$v_Pois
}
matplot(ve,
type = "l",
lwd = 2,
col = c(myred, myblue, mygreen),
bty = "n")
legend("topright",
legend = c(expression(hat(theta)[n]), expression(tilde(theta)[n]), expression(dot(theta)[n])),
col = c(myred, myblue, mygreen),
lty = 1,
lwd = 2,
bty = "n",
seg.len = 1.5)Estimare prin metoda verosimilității maxime
Exemplu: EVM nu este întotdeauna media eșantionului chiar dacă \(\mathbb{E}_{\theta}[\hat{\theta}_n] = \theta\)
Exercițiul 3.1 Fie \(X_1,X_2,\ldots,X_n\) un eșantion de talie \(n\) dintr-o populație Laplace \(L(\theta, c)\) a cărei densitate este dată de formula
\[ f_{\theta, c}(x) = \frac{1}{2c}e^{-\frac{|x-\theta|}{c}}, \quad -\infty<x<\infty \]
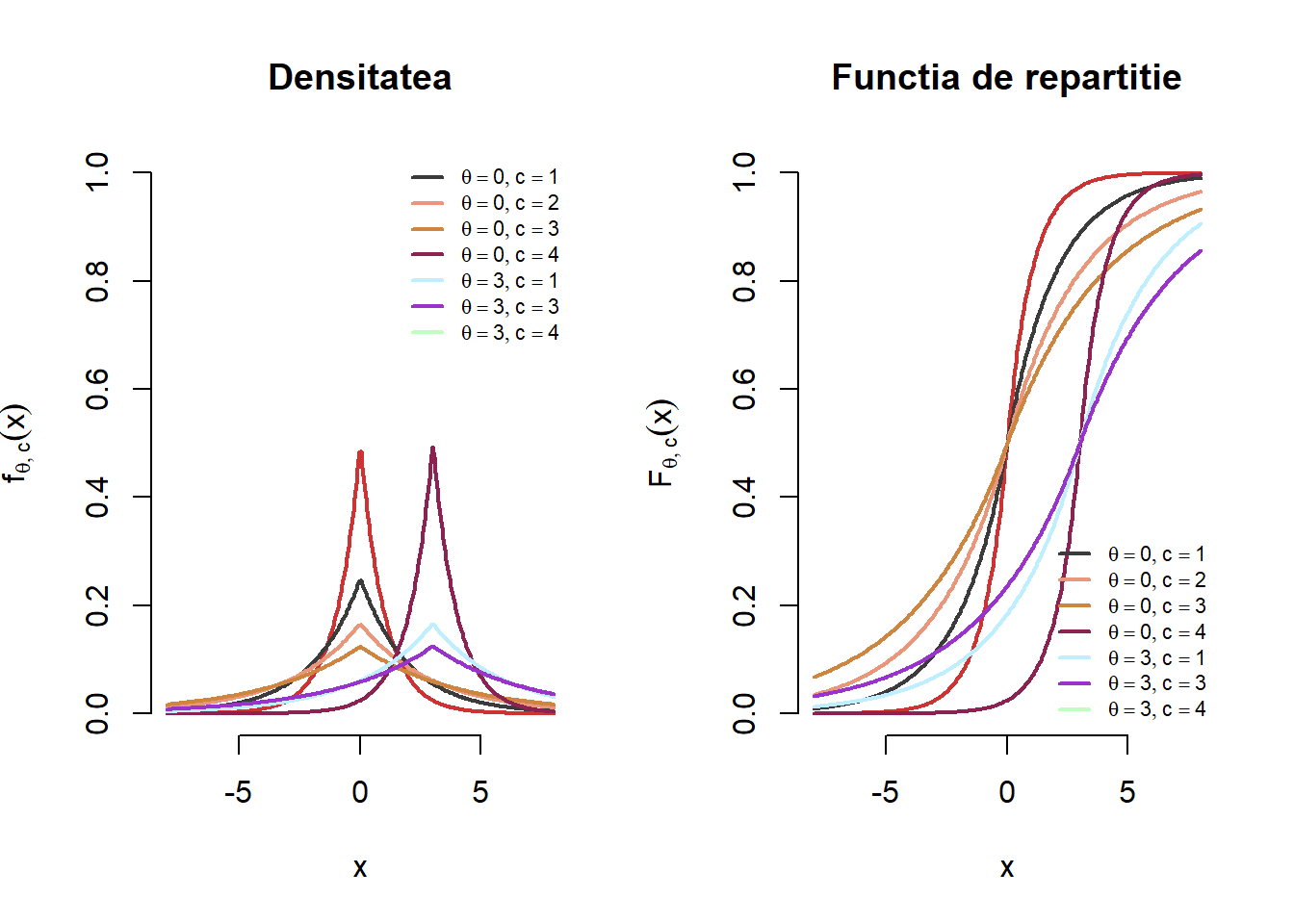
Ilustrați grafic densitatea și funcția de repartiție a repartiției Laplace pentru diferite valori ale parametrilor \(\theta\) (de locație) și \(c\) (de scală), e.g. \(\theta\in\{0, 3\}\) și \(c\in\{1,2,3,4\}\).
Determinați estimatorul de verosimilitate maximă \(\hat{\theta}_n\) pentru \(\theta\).
Soluție. Avem:
- Se poate arăta cu ușurință (am văzut în ?@exr-stat-sim-minv-cont-e7) că funcția de repartiție a repartiției \(\mathrm{Laplace}(\theta, c)\) este
\[ F_{\theta, c}(x) = \frac{1}{2} + \frac{1}{2}\operatorname{sgn}(x-\theta)\left(1-e^{-\frac{|x-\theta|}{c}}\right) = \left\{\begin{array}{ll} \frac{1}{2}e^{-\frac{|x-\theta|}{c}}, & x<\theta\\ 1-\frac{1}{2}e^{-\frac{|x-\theta|}{c}}, & x\geq\theta \end{array}\right. \]
În Figura 3.1 ilustrăm grafic pentru o serie de parametrii \((\theta,c)\) densitatea și funcția de repartiție pentru repartiția \(\mathrm{Laplace}(\theta, c)\):
- Pentru a determina estimatorul de verosimilitate maximă să observăm că funcția de verosimilitate este
\[ L_n(\theta|\mathbf{X}) = \prod_{i=1}^{n}\left(\frac{1}{2c}e^{-\frac{|X_i-\theta|}{c}}\right) = \frac{1}{(2c)^n}e^{-\sum_{i=1}^{n}\frac{|X_i-\theta|}{c}} \]
și acesta ia valoarea maximă pentru toate valorile lui \(\theta\) care minimizează funcția de la exponent
\[ M(\theta) = \sum_{i=1}^{n}|X_i-\theta| = \sum_{i=1}^{n}|X_{(i)}-\theta|, \]
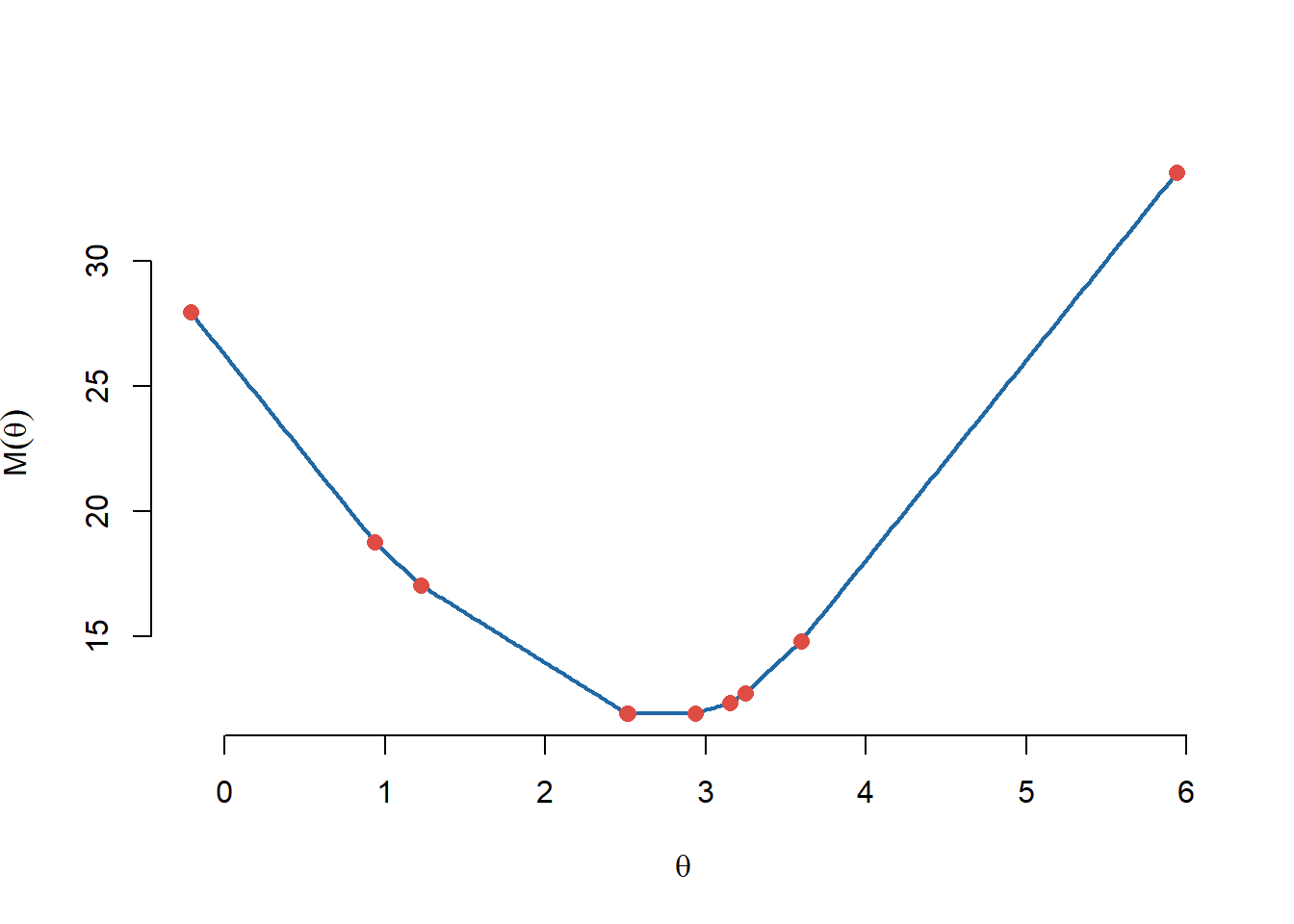
unde \(x_{(i)}\) este statistica de ordine de rang \(i\). Se poate vedea că funcția \(M(\theta)\) este continuă și afină pe porțiuni din Figura 3.2 de mai jos (pentru un eșantion de volum \(10\) dintr-o populație \(\mathrm{Laplace}(3,1)\) - creați o funcție care vă permite să generați observații repartizate Laplace).
rLaplace <- function (n, mu = 0, b = 1)
{
u <- runif(n) - 0.5
x <- mu - b * sign(u) * log(1 - 2 * abs(u))
return(x)
}
theta0 <- 3
b <- 1
set.seed(333)
x <- rLaplace(10, mu = theta0, b = b)
M_theta <- function(x, theta){
sapply(theta, function(t){sum(abs(x-t))})
}
theta <- seq(min(x), max(x), length.out = 500)
M <- M_theta(x, theta)
plot(theta, M, type = "l",
xlab = TeX("$\\theta$"),
ylab = TeX("$M(\\theta)$"),
bty = "n", lwd = 2,
col = myblue)
points(x, M_theta(x, x),
pch = 16,
cex = 1.2,
col = myred)Observăm că dacă \(\theta\) se află între statistica de ordine de rang \(m\) și cea de rang \(m+1\), i.e. \(X_{(m)}\leq \theta\leq X_{(m+1)}\), atunci am avea că \(X_{(i)} \leq X_{(m)} \leq \theta\) dacă \(i\leq m\) și \(\theta\leq X_{(m+1)}\leq X_{(i)}\) dacă \(m+1\leq i\leq n\), prin urmare
\[ M(\theta) = \sum_{i=1}^{n}|X_{(i)}-\theta| = \sum_{i=1}^{m}(\theta - X_{(i)}) + \sum_{i=m+1}^{n}(X_{(i)}-\theta) \]
deci dacă \(X_{(m)}< \theta< X_{(m+1)}\) atunci
\[ \frac{d}{d\theta}M(\theta) = m - (n-m) = 2m-n. \]
Astfel, \(M'(\theta)<0\) (și \(M(\theta)\) este descrescătoare) dacă \(m<\frac{n}{2}\) și \(M'(\theta)>0\) (și \(M(\theta)\) este crescătoare) dacă \(m>\frac{n}{2}\). Dacă \(n = 2k+1\) este impar, atunci \(\frac{n}{2} = k +\frac{1}{2}\) iar \(M(\theta)\) este strict descrescătoare dacă \(\theta<X_{(k+1)}\) și strict crescătoare dacă \(\theta>X_{(k+1)}\) de unde deducem că minimul se atinge pentru \(\theta = X_{(k+1)}\).
Dacă \(n = 2k\) este par atunci, raționând asemănător, deducem că \(M(\theta)\) este minimizată pentru orice punct din intervalul \((X_{(k)}, X_{(k+1)})\), deci orice punct din acest interval va maximiza și funcția de verosimilitate. Prin convenție alegem estimatorul de verosimilitate maximă să fie mijlocul acestui interval, i.e. \(\theta = \frac{X_{(k)} + X_{(k+1)}}{2}\).
Prin urmare am găsit că estimatorul de verosimilitate maximă este mediana eșantionului
\[ \hat{\theta}_n = \left\{\begin{array}{ll} X_{\left(\frac{n+1}{2}\right)}, & \text{$n$ impar}\\ \frac{X_{\left(\frac{n}{2}\right)} + X_{\left(\frac{n}{2}+1\right)}}{2}, & \text{$n$ par}\\ \end{array}\right. \]
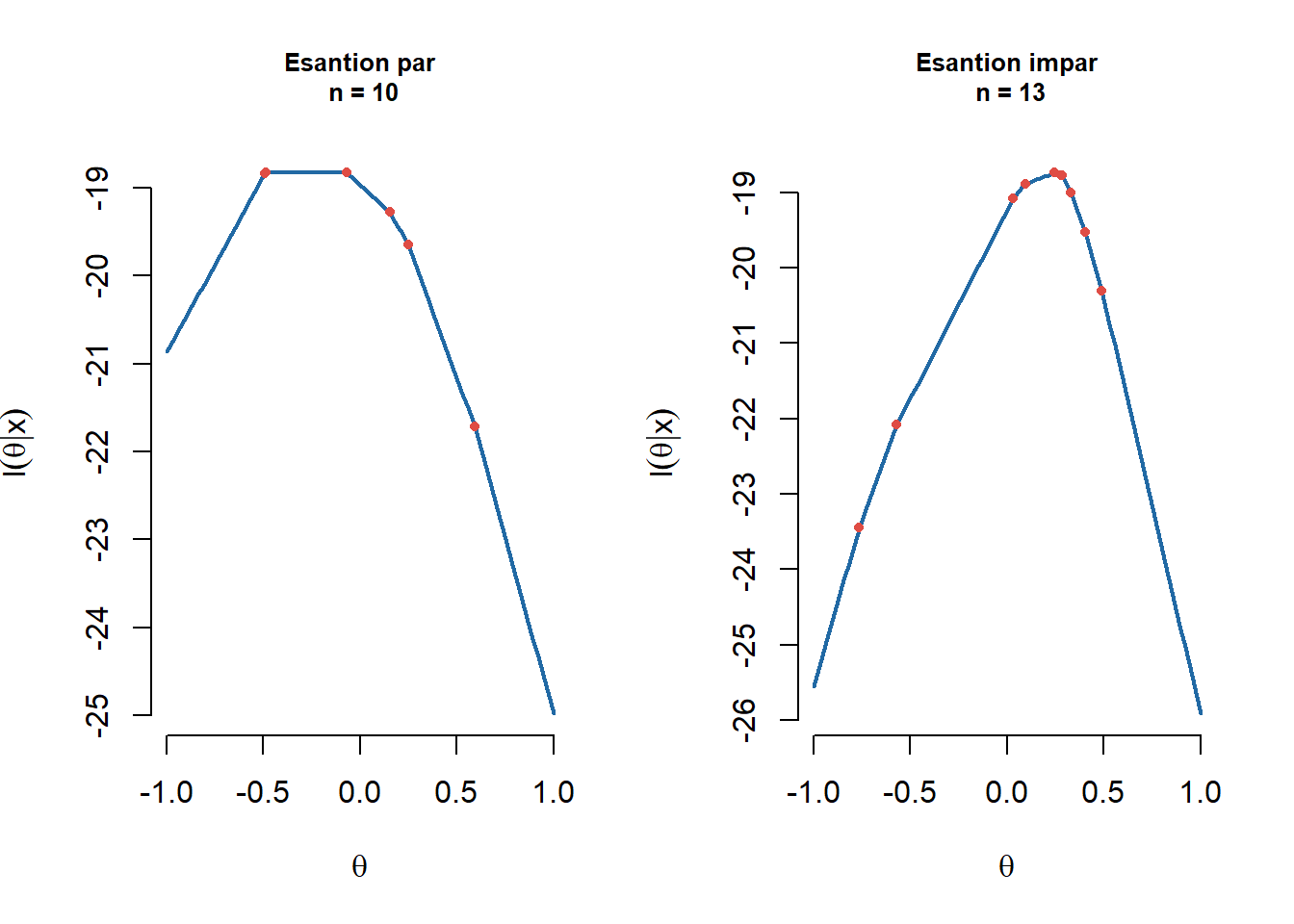
În Figura 3.3 avem ilustrat logaritmul funcției de verosimilitate pentru un eșantion de volum par (stânga) și unul de volum impar (dreapta):
theta0 <- 0
b <- 1
logLikelihoodLaplace <- function(x, theta, b){
sapply(theta, function(t){
-length(x)*log(2*b)-sum(abs(x-t))})
}
par(mfrow = c(1,2))
# Esantion par
n <- 10
set.seed(333)
x <- rLaplace(n, mu = theta0, b = b)
theta <- seq(-1,1, length.out = 100)
y <- logLikelihoodLaplace(x, theta, b)
plot(theta, y, type = "l",
bty = "n", lwd = 2,
col = myblue,
xlab = TeX("$\\theta$"),
ylab = TeX("$l(\\theta | x)$"),
main = paste0("Esantion par\n n = ", n),
cex.main = 0.8)
points(x, logLikelihoodLaplace(x, x, b),
pch = 16,
col = myred,
cex = 0.7)
# Esantion impar
n <- 13
set.seed(1234)
x <- rLaplace(n, mu = theta0, b = b)
theta <- seq(-1,1, length.out = 100)
y <- logLikelihoodLaplace(x, theta, b)
plot(theta, y, type = "l",
bty = "n", lwd = 2,
col = myblue,
xlab = TeX("$\\theta$"),
ylab = TeX("$l(\\theta | x)$"),
main = paste0("Esantion impar\n n = ", n),
cex.main = 0.8)
points(x, logLikelihoodLaplace(x, x, b),
pch = 16,
col = myred,
cex = 0.7)Exemplu de EVM determinat prin soluții numerice
Exercițiul 3.2 Fie \(X_1,X_2,\ldots,X_n\) un eșantion de talie \(n\) dintr-o populație logistică a cărei densitate este dată de formula
\[ f_{\theta}(x) = \frac{e^{-(x-\theta)}}{\left(1+e^{-(x-\theta)}\right)^2}, \quad x\in\mathbb{R},\, \theta\in\mathbb{R} \]
Determinați estimatorul de verosimilitate maximă \(\hat{\theta}_n\) pentru \(\theta\).
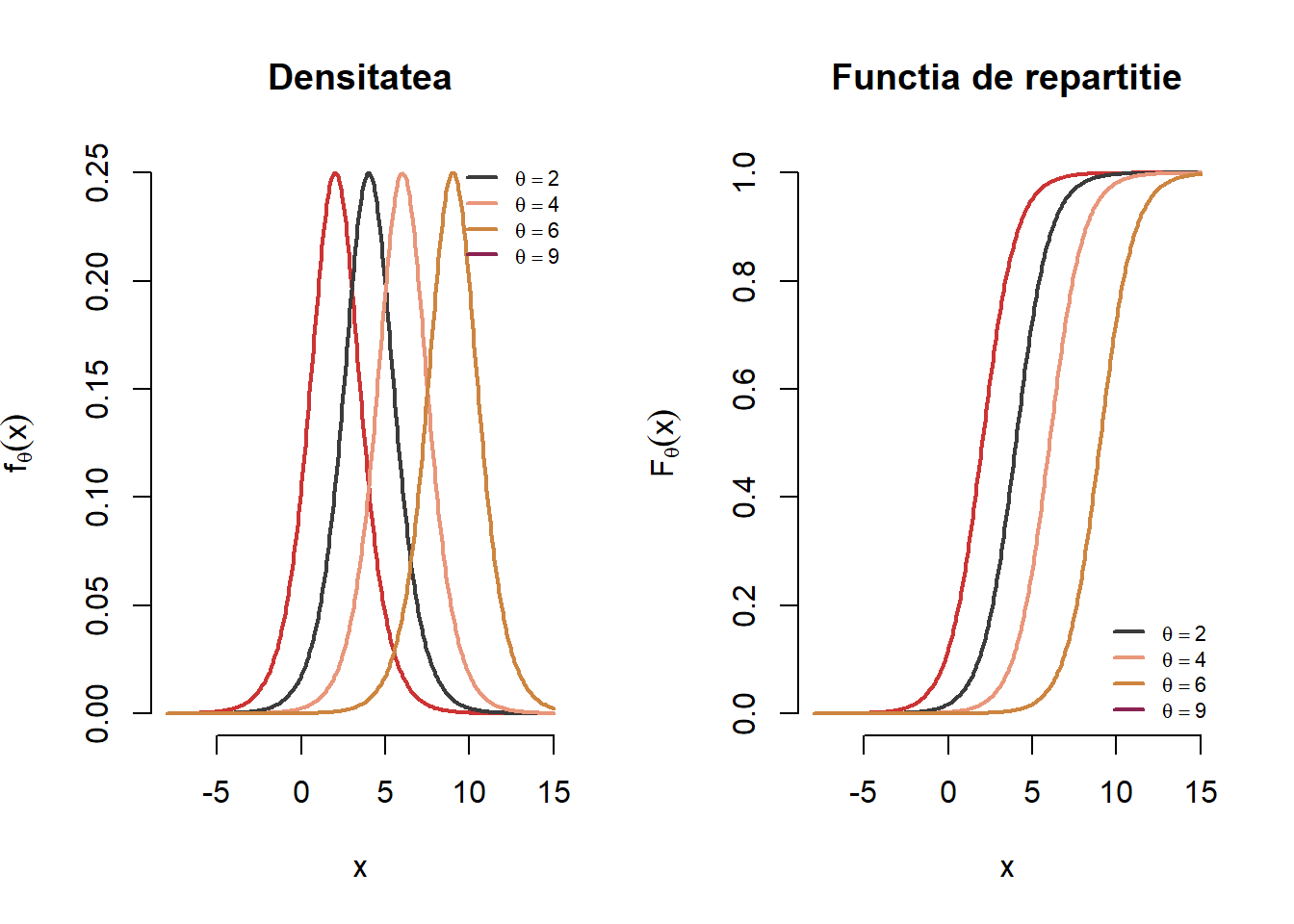
Soluție. Densitatea de repartiție și funcția de repartiție a repartiției logistice sunt ilustrate mai jos (în R se folosesc funcțiile: rlogis, dlogis, plogis și respectiv qlogis):
Observăm că funcția de verosimilitate este dată de
\[ L_n(\theta|\mathbf{x}) = \prod_{i=1}^{n}f_{\theta}(x_i) = \prod_{i=1}^{n}\frac{e^{-(x_i-\theta)}}{\left(1+e^{-(x_i-\theta)}\right)^2} \]
iar logaritmul funcției de verosimilitate este
\[ l_n(\theta|\mathbf{x}) = \sum_{i=1}^{n}\log{f_{\theta}(x_i)} = n\theta - n\bar{x}_n - 2\sum_{i=1}^{n}\log{\left(1+e^{-(x_i-\theta)}\right)}. \]
Pentru a găsi valoarea lui \(\theta\) care maximizează logaritmul funcției de verosimilitate și prin urmare a funcției de verosimilitate trebuie să rezolvăm ecuația \(l'(\theta|\mathbf{x}) = 0\), unde derivata lui \(l(\theta|\mathbf{x})\) este
\[ l_n'(\theta|\mathbf{x}) = n - 2\sum_{i = 1}^{n}\frac{e^{-(x_i-\theta)}}{1+e^{-(x_i-\theta)}} \]
ceea ce conduce la ecuația
\[ \sum_{i = 1}^{n}\frac{e^{-(x_i-\theta)}}{1+e^{-(x_i-\theta)}} = \frac{n}{2} \tag{$\star$} \]
Chiar dacă această ecuație nu se simplifică, se poate arăta că această ecuația admite soluție unică. Observăm că derivata parțiala a membrului drept în (\(\star\)) devine
\[ \frac{\partial }{\partial \theta}\sum_{i = 1}^{n}\frac{e^{-(x_i-\theta)}}{1+e^{-(x_i-\theta)}} = \sum_{i = 1}^{n}\frac{e^{-(x_i-\theta)}}{\left(1+e^{-(x_i-\theta)}\right)^2}>0 \]
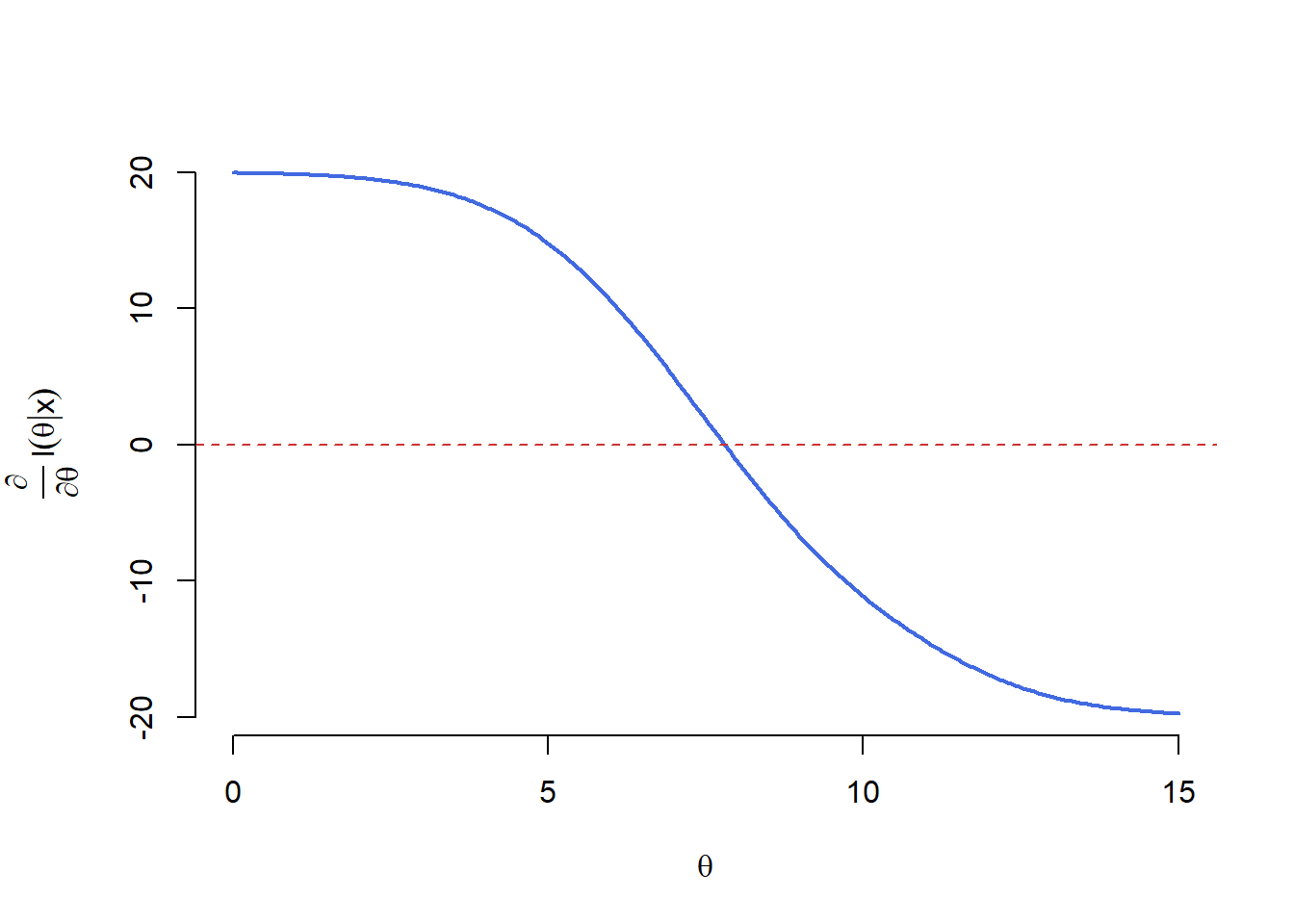
ceea ce arată că membrul stâng este o funcție strict crescătoare în \(\theta\). Cum membrul stâng în (\(\star\)) tinde spre \(0\) atunci când \(\theta\to-\infty\) și spre \(n\) pentru \(\theta\to\infty\) deducem că ecuația (\(\star\)) admite soluție unică (vezi graficul de mai jos).
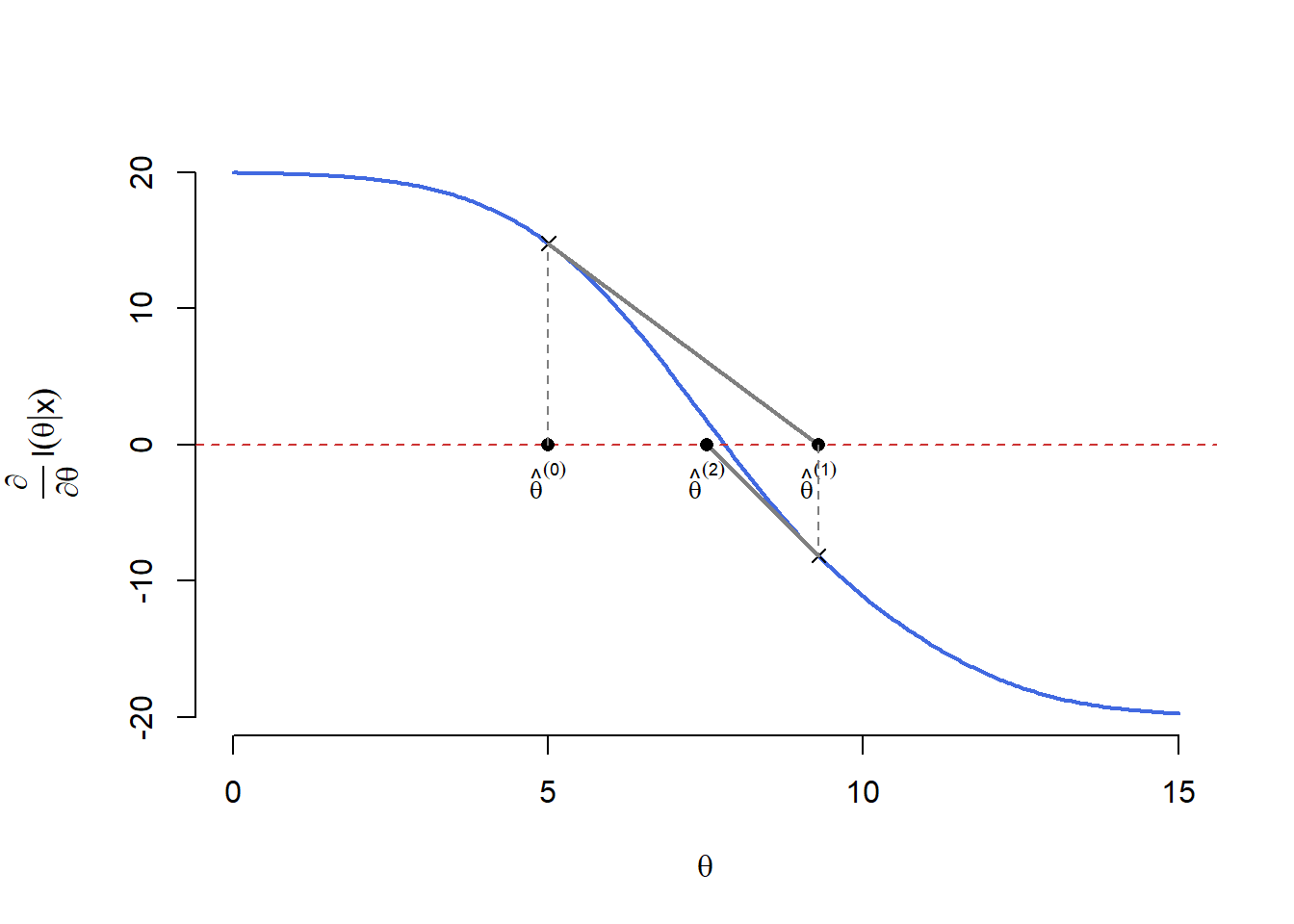
Cum nu putem găsi o soluție a ecuației \(l_n'(\theta|\mathbb{x}) = 0\) sub formă compactă, este necesar să apelăm la metode numerice. O astfel de metodă numerică este binecunoscuta metodă a lui Newton-Raphson. Metoda presupune să începem cu o valoare (soluție) inițială \(\hat{\theta}^{(0)}\) și să alegem, plecând de la aceasta, o nouă valoare \(\hat{\theta}^{(1)}\) definită prin
\[ \hat{\theta}^{(1)} = \hat{\theta}^{(0)} - \frac{l_n'\left(\hat{\theta}^{(0)}\right)}{l_n''\left(\hat{\theta}^{(0)}\right)}, \]
adică \(\hat{\theta}^{(1)}\) este intersecția cu axa absciselor a tangentei în punctul \(\left(\hat{\theta}^{(0)}, l_n'\left(\hat{\theta}^{(0)}\right)\right)\) la graficul funcției \(l_n'(\theta)\). Ideea este de a itera procesul până când soluția converge, cu alte cuvinte pornind de la o valoare rezonabilă de start \(\hat{\theta}^{(0)}\) la pasul \(k+1\) avem
\[ \hat{\theta}^{(k+1)} = \hat{\theta}^{(k)} - \frac{l_n'\left(\hat{\theta}^{(k)}\right)}{l_n''\left(\hat{\theta}^{(k)}\right)} \]
și oprim procesul atunci când \(k\) este suficient de mare și/sau \(\left|\hat{\theta}^{(k+1)} - \hat{\theta}^{(k)}\right|\) este suficient de mic. Următorul grafic ilustrează grafic algoritmul lui Newton:
Obs: Singurul lucru care se schimbă atunci când trecem de la scalar la vector, este funcția \(l_n(\theta)\) care acum este o funcție de \(p>1\) variabile, \(\theta = (\theta_1, \theta_2, \ldots, \theta_p)^{\intercal}\in\mathbb{R}^p\). În acest context \(l'(\theta)\) este un vector de derivate parțiale iar \(l''(\theta)\) este o matrice de derivate parțiale de ordin doi. Prin urmare iterațiile din metoda lui Newton sunt
\[ \hat{\theta}^{(k+1)} = \hat{\theta}^{(k)} - \left[l_n''\left(\hat{\theta}^{(k)}\right)\right]^{-1}l_n'\left(\hat{\theta}^{(k)}\right) \]
unde \([\cdot]^{-1}\) este pseudoinversa unei matrice.
Funcția de mai jos implementează metoda lui Newton pentru cazul multidimensional:
# Metoda lui Newton
newton <- function(f, df, x0, eps=1e-08, maxiter=1000, ...) {
# in caz ca nu e incarcat pachetul sa putem accesa pseudoinversa
if(!exists("ginv")) library(MASS)
x <- x0
k <- 0
repeat {
k <- k + 1
x.new <- x - as.numeric(ginv(df(x, ...)) %*% f(x, ...))
if(mean(abs(x.new - x)) < eps | k >= maxiter) {
if(k >= maxiter) warning("S-a atins numarul maxim de iteratii!")
break
}
x <- x.new
}
out <- list(solution = x.new, value = f(x.new, ...), iter = k)
return(out)
}Să presupunem că am observat următorul eșantion de volum \(20\) din repartiția logistică:
[1] 6.996304 9.970107 12.304991 11.259549 6.326912 5.378941 4.299639
[8] 8.484635 5.601117 7.094335 6.324731 6.868456 9.753360 8.042095
[15] 8.227830 10.977982 7.743096 7.722159 8.562884 6.968356set.seed(112)
x <- rlogis(20, location = 7.5)
n <- length(x)
dl <- function(theta) n - 2 * sum(exp(theta - x) / (1 + exp(theta - x)))
ddl <- function(theta) {-2 * sum(exp(theta - x) / (1 + exp(theta - x))^2)}
logis.newton <- newton(dl, ddl, median(x))și aplicând metoda lui Newton găsim estimatorul de verosimilitate maximă \(\hat{\theta}_n=\) 7.7933 după numai 3 iterații (datele au fost simulate folosind \(\theta = 7.5\)).