Elemente de statistică descriptivă în R

Media eșantionului

În cele ce urmează vom introduce noțiunea de medie a eșantionului:

Definiția 1.1 (Media eșantionului) Fie \(X_1,X_2,\ldots,X_n\) un eșantion de volum \(n\) dintr-o populație a cărei funcție de repartiție este \(F\). Se numește media empirică sau media eșantionului statistica

\[ \bar{X}_n = \frac{1}{n}\sum_{i=1}^{n}X_i \]

Vom preciza în continuare o serie de proprietăți ale mediei eșantionului:

Propoziția 1.1 (Proprietățile mediei eșantionului) Fie \(X_1, X_2, \ldots X_n\) un eșantion de volum \(n\) dintr-o populație de medie \(\mu=\mathbb{E}\left[X_1\right]<\infty\) și dispersie (varianță) \(\sigma^2=\operatorname{Var}(X)<\infty\). Atunci:

1. \(\mathbb{E}\left[\bar{X}_n\right]=\mu\) și \(\operatorname{Var}\left(\bar{X}_n\right)=\sigma^2 / n\)
2. \(\bar{X}_n \xrightarrow{\text { a.s }} \mu\) și \(\sqrt{n}\left(\bar{X}_n-\mu\right) \xrightarrow{d} N\left(0, \sigma^2\right)\)

Demonstrație. Avem

1. Ținând cont că \(\bar{X}_{n}=\frac{1}{n} \sum_{i=1}^{n} X_{i}\), și din liniaritatea mediei găsim că

\[ \mathbb{E}\left[\bar{X}_{n}\right]=\frac{1}{n} \sum_{i=1}^{n} \mathbb{E}\left[X_{i}\right]=\mu \]

În plus, pentru calculul varianței obținem

\[ \begin{aligned} \operatorname{Var}\left(\bar{X}_n\right) &= \operatorname{Var}\left(\frac{1}{n} \sum_{i=1}^n X_i\right)=\frac{1}{n^2} \operatorname{Var}\left(\sum_{i=1}^n X_i\right)\\ & \overset{indep.}{=}\frac{1}{n^2} \sum_{i=1}^n \underbrace{\operatorname{Var}\left(X_i\right)}_{\sigma^2}=\frac{\sigma^2}{n} \end{aligned} \]

2. Aplicând Legea Numerelor Mari șirului \(X_1, X_2, \ldots X_n,\ldots\) avem că

\[ \bar{X}_{n} \xrightarrow[n \rightarrow \infty]{\text{a.s.}} \mu \]

și din Teorema Limită Centrală rezultă că

\[ \sqrt{n}\left(\bar{X}_{n}-\mu\right) \xrightarrow[n \rightarrow \infty]{d} \mathcal{N}\left(0, \sigma^{2}\right) \]

Varianța empirică și varianța eșantionului

Definiția 2.1 (Varianța empirică și varianța eșantionului) Fie \(X_1,X_2,\ldots,X_n\) un eșantion de volum \(n\) dintr-o populație a cărei funcție de repartiție este \(F\). Se numește varianța empirică statistica \(V_n^2\) definită prin

\[ V_n^2 = \frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}_n\right)^2 \]

și varianța eșantionului statistica \(S_n^2\) definită prin

\[ S_n^2 = \frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}_n\right)^2. \]

Varianța empirică și a eșantionului verifică următoarele proprietăți

Propoziția 2.1 (Proprietățile varianței eșantionului) Fie \(X_1, X_2, \ldots X_n\) un eșantion de volum \(n\) dintr-o populație de medie \(\mu=\mathbb{E}\left[X_1\right]<\infty\) și dispersie (varianță) \(\sigma^2=\operatorname{Var}(X)<\infty\). Atunci

1. \(\mathbb{E}\left[V_n^2\right]=\frac{n-1}{n}\sigma^2\) și \(\mathbb{E}\left[S_n^2\right]=\sigma^2\)
2. \(V_n^2 \xrightarrow{\text { a.s }} \sigma^2\) și \(S_n^2 \xrightarrow{\text { a.s }} \sigma^2\)
3. În plus dacă există \(\mathbb{E}\left[\left(X_1 - \mu\right)^4\right]\) și este finit, atunci \(\sqrt{n}\left(V_n^2-\sigma^2\right) \xrightarrow{d} N\left(0, \tau^4 - \sigma^4\right)\) și respectiv \(\sqrt{n}\left(S_n^2-\sigma^2\right) \xrightarrow{d} N\left(0, \tau^4 - \sigma^4\right)\)

Demonstrație. Cum \(\operatorname{Var}(X)=\mathbb{E}\left[(X-\mu)^{2}\right]\), un estimator natural al varianței este

\[ \frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2} \]

și cum \(\mu\) nu este cunoscut îl înlocuim cu estimatorul \(V_n^2\).

1. Adunând și scăzând \(\mu\) obținem

\[ \begin{aligned} n V_{n}^{2} & =\sum_{i=1}^{n}\left(\left(X_{i}-\mu\right)+\left(\mu-\bar{X}_{n}\right)\right)^{2} \\ & =\sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}+2 \sum_{i=1}^{n}\left(X_{i}-\mu\right)\left(\mu-\bar{X}_{n}\right)+\sum_{i=1}^{n}\left(\mu-\bar{X}_{n}\right)^{2} \\ & =\sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}+2\left(\mu-\bar{X}_{n}\right) \sum_{i=1}^{n}\left(X_{i}-\mu\right)+n\left(\mu-\bar{X}_{n}\right)^{2} \\ & =\sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}+2\left(\mu-\bar{X}_{n}\right) n\left(\bar{X}_{n}-\mu\right)+n\left(\mu-\bar{X}_{n}\right)^{2} \\ & =\sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}-n\left(\mu-\bar{X}_{n}\right)^{2} \end{aligned} \]

iar din liniaritatea mediei și descompunerea precedentă avem că

\[ \begin{aligned} \mathbb{E}\left[V_{n}^{2}\right] & =\mathbb{E}\left[\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}-\left(\bar{X}_{n}-\mu\right)^{2}\right] \\ & =\frac{1}{n} \sum_{i=1}^{n} \mathbb{E}\left[\left(X_{i}-\mu\right)^{2}\right]-\mathbb{E}\left[\left(\bar{X}_{n}-\mu\right)^{2}\right] \\ & =\frac{1}{n} \sum_{i=1}^{n} \operatorname{Var}\left(X_{i}\right)-\operatorname{Var}\left(\bar{X}_{n}\right) \\ & =\frac{n-1}{n} \sigma^{2} \end{aligned} \]

Ținând cont că \(S_n^2 = \frac{n}{n-1}V_n^2\) deducem că \(\mathbb{E}\left[S_{n}^{2}\right] = \sigma^2\).

2. Având în vedere că \(S_n^2 = \frac{n}{n-1}V_n^2\) și cum \(\frac{n}{n-1}\to1\) este suficient să arătăm rezultatul pentru \(V_n^2\). Folosind descompunerea

\[ V_{n}^{2} = \frac{1}{n} \sum_{i=1}^{n}X_{i}^{2}-\bar{X}_{n}^{2} \]

și utilizând Legea Numerelor Mari pentru șirul \((X_n)_n\) deducem că \(\bar{X}_{n} \xrightarrow[n \rightarrow \infty]{\text{a.s.}} \mu\) și din Teorema Aplicațiilor Continue (folosind \(g(x)=x^2\)) rezultă \(\bar{X}_{n}^2 \xrightarrow[n \rightarrow \infty]{\text{a.s.}} \mu^2\). În plus, aplicând Legea Numerelor Mari pentru șirul \((X_n^2)_n\) obținem că \(\frac{1}{n} \sum_{i=1}^{n}X_{i}^{2}\xrightarrow[n \rightarrow \infty]{\text{a.s.}}\mathbb{E}[X_1^2]\) ceea ce implică

\[ V_{n}^{2} = \frac{1}{n} \sum_{i=1}^{n}X_{i}^{2}-\bar{X}_{n}^{2}\xrightarrow[n \rightarrow \infty]{\text{a.s.}}\mathbb{E}[X_1^2] - \mu^2 = \sigma^2. \]

3. Din descompunerea

\[ V_{n}^{2} = \frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}-\left(\bar{X}_{n}-\mu\right)^{2} \]

putem aplica Teorema Limită Centrală primului termen și obținem

\[ \sqrt{n}\left(\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}-\sigma^{2}\right) \xrightarrow[n \rightarrow \infty]{d} \mathcal{N}\left(0, \tau^{4}-\sigma^{4}\right) \]

unde am ținut cont că \(\mathbb{E}\left[\left(X_{i}-\mu\right)^{2}\right]=\sigma^2\) și \(\operatorname{Var}\left(\left(X_{i}-\mu\right)^{2}\right) = \tau^4 - \sigma^4\).

Pentru al doilea termen,

\[ \sqrt{n}\left(\bar{X}_{n}-\mu\right)^{2}=\left(\sqrt{n}\left(\bar{X}_{n}-\mu\right)\right)\left(\bar{X}_{n}-\mu\right) . \]

și din Teorema Limită Centrală avem

\[ \sqrt{n}\left(\bar{X}_{n}-\mu\right) \xrightarrow[n \rightarrow+\infty]{d} \mathcal{N}\left(0, \sigma^{2}\right) . \]

În plus, cum \(\bar{X}_{n}-\mu\) converge în probabilitate la \(0\), prin aplicarea Teoremei lui Slutsky găsim

\[ \sqrt{n}\left(\bar{X}_{n}-\mu\right)^{2} \xrightarrow[n \rightarrow \infty]{d} 0 \]

și cum convergența în distribuție la o constantă implică convergența în probabilitate avem \(\sqrt{n}\left(\bar{X}_{n}-\mu\right)^{2} \xrightarrow[n \rightarrow \infty]{\mathbb{P}} 0\).

Alternativ, putem arăta această convergență și aplicând inegalitatea lui Markov. Astfel, pentru \(\epsilon>0\) avem

\[ \mathbb{P}\left[\sqrt{n}\left(\bar{X}_{n}-\mu\right)^{2} \geq \epsilon\right] \leq \frac{\sqrt{n} \mathbb{E}\left[\left(\bar{X}_{n}-\mu\right)^{2}\right]}{\epsilon}=\frac{\sigma^{2}}{\sqrt{n} \epsilon} \]

de unde \(\sqrt{n}\left(\bar{X}_{n}-\mu\right)^{2} \xrightarrow[n \rightarrow \infty]{\mathbb{P}} 0\).

Aplicând acum Teorema lui Slutsky obținem

\[ \sqrt{n}\left(V_{n}^{2}-\sigma^{2}\right) \xrightarrow[n \rightarrow \infty]{d} \mathcal{N}\left(0, \tau^{4}-\sigma^{4}\right) . \]

Ținând cont că \(S_{n}^{2}=\frac{n}{n-1} V_{n}^{2}\), avem că

\[ \sqrt{n}\left(S_{n}^{2}-\sigma^{2}\right)=\sqrt{n}\left(\frac{n}{n-1}V_{n}^{2}-\sigma^{2}\right)=\sqrt{n}\left(V_{n}^{2}-\sigma^{2}\right)+\frac{\sqrt{n}}{n-1} V_{n}^{2} \]

și ținând cont că \(\sqrt{n}\left(V_{n}^{2}-\sigma^{2}\right)\) converge în distribuție din punctul anterior și cum \(V_{n}^{2}\) converge în probabilitate la \(\sigma^{2}\) iar \(\frac{\sqrt{n}}{n-1}\) converge la \(0\), termenul \(\frac{\sqrt{n}}{n-1} V_{n}^{2}\) converge în probabilitate la \(0\), prin urmare aplicând Teorema lui Slutsky deducem că

\[ \sqrt{n}\left(S_{n}^{2}-\sigma^{2}\right) \xrightarrow[n \rightarrow \infty]{d} \mathcal{N}\left(0,\tau^4 - \sigma^{4}\right). \]

Rezultatul anterior nu ne spune nimic despre varianța varianței empirice. Următoarea propoziție rezolvă această problemă

Propoziția 2.2 (Varianța varianței eșantionului) Fie \(X_1,\dots,X_n\) un eșantion de volum \(n\) dintr-o populație de medie \(\mu\) și varianță \(\sigma^2\). Arătați că varianța varianței eșantionului este:

\[ Var(S_n^2) = \frac{1}{n}\left(\mu_4-\frac{n-3}{n-1}\sigma^4\right) \]

unde \(\mu_4=\mathbb{E}[(X_i-\mu)^4]\) este momentul centrat de ordin \(4\).

Demonstrație. Am văzut la curs că

\[ (n-1)S_n^2=\sum_{i=1}^{n}(X_i-\bar{X})^2 = \sum_{i=1}^{n}(X_i-\mu)^2 - n(\bar{X}-\mu)^2 = \sum_{i=1}^{n}(X_i-\mu)^2 - \frac{1}{n}\left[\sum_{i=1}^{n}(X_i-\mu)\right]^2. \]

Dacă notăm cu \(Z_i = X_i-\mu\) atunci observăm că v.a. \(Z_i\) sunt i.i.d. iar \(\mathbb{E}[Z_i]=0\), \(\mathbb{E}[Z_i^2]=\sigma^2\) și \(\mathbb{E}[Z_i^4]=\mu_4\). Avem că

\[\begin{align*} (n-1)S_n^2 &= \sum_{i=1}^{n}(Z_i)^2 - \frac{1}{n}\left(\sum_{i=1}^{n}Z_i\right)^2 = \sum_{i=1}^{n}(Z_i)^2 - \frac{1}{n}\left(\sum_{i=1}^{n}Z_i^2+2\mathop{\sum\sum}_{i<j}Z_iZ_j\right)^2 \\ &= \frac{n-1}{n}\sum_{i=1}^{n}(Z_i)^2-\frac{2}{n}\mathop{\sum\sum}_{i<j}Z_iZ_j \end{align*}\]

de unde obținem \[ \begin{aligned} (n-1)^2\mathbb{E}[(S_n^2)^2] &= \mathbb{E}\left[\left(\frac{n-1}{n}\sum_{i=1}^{n}(Z_i)^2-\frac{2}{n}\mathop{\sum\sum}_{i<j}Z_iZ_j\right)^2\right] \notag \\ &= \left(\frac{n-1}{n}\right)^2\mathbb{E}\left[\sum_{i=1}^{n}Z_i^4+2\mathop{\sum\sum}_{i<j}Z_i^2Z_j^2\right] \notag \\ &-\frac{4(n-1)}{n^2}\mathbb{E}\left[\left(\sum_{k=1}^{n}Z_k^2\right)\left(\mathop{\sum\sum}_{i<j}Z_iZ_j\right)\right] +\frac{4}{n^2}\mathbb{E}\left[\left(\mathop{\sum\sum}_{i<j}Z_iZ_j\right)^2\right] \end{aligned} \tag{2.1}\]

Pentru primul termen din suma de mai sus avem

\[ \left(\frac{n-1}{n}\right)^2\mathbb{E}\left[\sum_{i=1}^{n}Z_i^4+2\mathop{\sum\sum}_{i<j}Z_i^2Z_j^2\right] = \left(\frac{n-1}{n}\right)^2\left(n\mu_4+n(n-1)\sigma^4\right). \]

Termenul al doilea din Ecuația 2.1 este \(0\) deoarece conține sau termeni de forma \(\mathbb{E}[Z_iZ_jZ_k^2]\), cu \(i\neq j\neq k\), sau termeni de forma \(\mathbb{E}[Z_jZ_k^3]\) cu \(j\neq k\).

Pentru ultimul termen avem din Ecuația 2.1 avem

\[ \frac{4}{n^2}\mathbb{E}\left[\left(\mathop{\sum\sum}_{i<j}Z_iZ_j\right)^2\right] = \frac{4}{n^2}\mathbb{E}\left[\mathop{\sum\sum}_{i<j}Z_i^2Z_j^2\right] = \frac{2(n-1)}{n}\sigma^4, \]

restul termenilor fiind zero deoarece sunt de forma \(\mathbb{E}[Z_i^2Z_jZ_k]\) sau \(\mathbb{E}[Z_iZ_jZ_kZ_l]\) cu \(i\neq j\neq k\neq l\).

Combinând rezultatele obținem că

\[\begin{align*} (n-1)^2Var[S_n^2] &= \frac{(n-1)^2}{n}\mu_4 + \frac{(n-1)^3}{n}\sigma^4 +2\frac{n-1}{n}\sigma^4-(n-1)^2\mathbb{E}[S_n^2]^2\\ &= \frac{(n-1)^2}{n}\mu_4 + \frac{(n-1)(3-n)}{n}\sigma^4 \end{align*}\]

prin urmare \(Var[S_n^2] = \frac{1}{n}\left(\mu_4-\frac{n-3}{n-1}\sigma^4\right)\).

În general, media eșantionului nu este independentă de varianța eșantionului (ca și în cazul normal). Următoarea propoziție ne spune care este covarianța dintre cei doi estimatori:

Propoziția 2.3 (Covarianța dintre media empirică și varianța eșantionului) Fie \(X_1,\dots,X_n\) un eșantion de volum \(n\) dintr-o populație de medie \(\mu\) și varianță \(\sigma^2\). Arătați că

\[ Cov(\bar{X}_n,S_n^2) = \frac{\mu_3}{n} \]

unde \(\mu_3=\mathbb{E}[(X_i-\mu)^3]\) este momentul centrat de ordin \(3\). Acest rezultat ne arată că cele două statistici sunt asimptotic necorelate.

Demonstrație. Dacă notăm cu \(Z_i=X_i-\mu\), atunci \(\bar{X}-\mu = \bar{Z}\) și \(\mathbb{E}[\bar{Z}]=0\). Mai mult,

\[ \sum_{i=1}^{n}(X_i-\bar{X})^2=\sum_{i=1}^{n}(Z_i-\bar{Z})^2=\sum_{i=1}^{n}Z_i^2-n\bar{Z}^2 \]

prin urmare

\[\begin{align*} Cov(\bar{X}_n,S_n^2) &= Cov(\bar{X}_n-\mu, S_n^2) = Cov\left(\bar{Z},\frac{1}{n-1}\left[\sum_{i=1}^{n}Z_i^2-n\bar{Z}^2\right]\right)\\ &= \frac{1}{n-1}\mathbb{E}\left[\bar{Z}\left(\sum_{i=1}^{n}Z_i^2-n\bar{Z}^2\right)\right] = \frac{1}{n-1}\left[\mathbb{E}\left[\bar{Z}\left(\sum_{i=1}^{n}Z_i^2\right)\right]-n\mathbb{E}[\bar{Z}^3]\right] \end{align*}\]

Cum

\[ \mathbb{E}\left[\bar{Z}\left(\sum_{i=1}^{n}Z_i^2\right)\right] = \frac{1}{n}\mathbb{E}\left[\left(\sum_{j=1}^{n}Z_j\right)\left(\sum_{i=1}^{n}Z_i^2\right)\right]=\frac{1}{n}\mathbb{E}\left[\sum_{i=1}^{n}Z_i^3\right] = \mu_3 \]

și

\[ \mathbb{E}[\bar{Z}^3] = \frac{1}{n^3}\mathbb{E}\left[\left(\sum_{i=1}^{n}Z_i\right)\left(\sum_{j=1}^{n}Z_j\right)\left(\sum_{k=1}^{n}Z_k\right)\right] = \frac{1}{n^3}\mathbb{E}\left[\sum_{i=1}^{n}Z_i^3\right] = \frac{\mu_3}{n^2} \]

rezultă că \(Cov(\bar{X}_n,S_n^2)=\frac{1}{n-1}\left(\mu_3-\frac{\mu_3}{n}\right) = \frac{\mu_3}{n}\).

Vom finaliza această secțiune prin ilustrarea proprietăților mediei și a varianței eșantionului în populații normale:

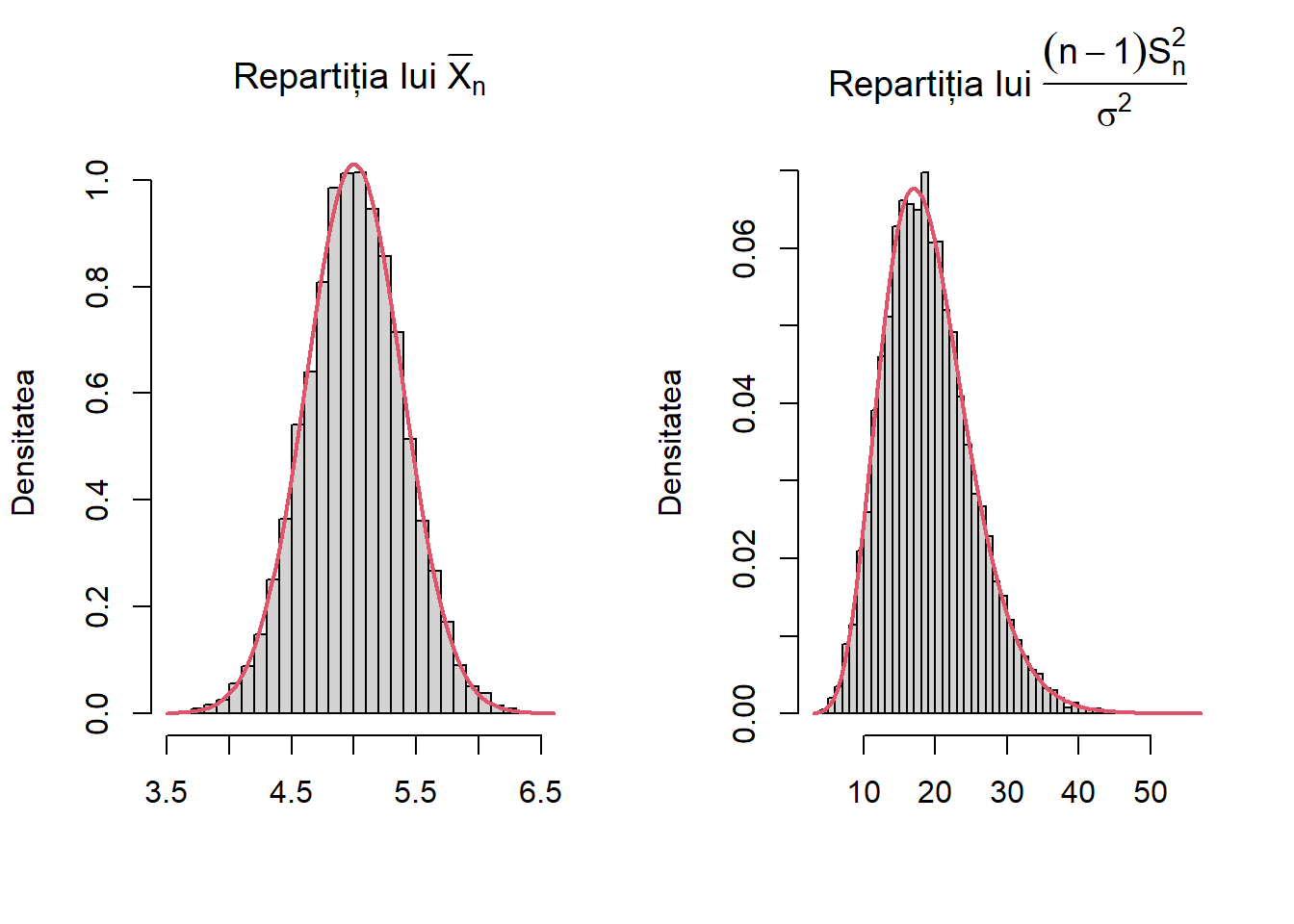
Propoziția 2.4 (Eșantionare în populații normale) Fie \(X_1,X_2,\ldots,X_n\) un eșantion de volum \(n\) dintr-o populație \(\mathcal{N}(\mu,\sigma^2)\) și considerăm \(\bar{X}_n\) și \(S_n^2\) media și respectiv varianța eșantionului. Atunci

1. \(\bar{X}_n\sim\mathcal{N}\left(\mu, \frac{\sigma^2}{n}\right)\)

2. \(\bar{X}_n\) și \(S_n^2\) sunt independente

3. \((n-1)\frac{S_n^2}{\sigma^2}\) este repartizată hi-pătrat cu \(n-1\) grade de libertate, i.e. \((n-1)\frac{S_n^2}{\sigma^2}\sim\chi^2\left(n-1\right)\)

Demonstrație. Pentru primul punct să observăm că din Propoziția 1.1 avem că \(\mathbb{E}\left[\bar{X}_n\right]=\mu\) și \(\operatorname{Var}\left(\bar{X}_n\right)=\sigma^2 / n\) și cum \(\bar{X}_n\) este repartizată normal, fiind o sumă de variabile aleatoare repartizate normal și independente, deducem că \(\bar{X}_n\sim\mathcal{N}\left(\mu, \frac{\sigma^2}{n}\right)\).

2. Vom presupune, fără a pierde din generalitate, că \(X_i\sim\mathcal{N}(0,1)\). Într-adevăr, dacă \(X_i\sim\mathcal{N}(\mu,\sigma^2)\) atunci putem scrie că \(X_i = \mu + \sigma Z_i\), unde \(Z_i\sim\mathcal{N}(0,1)\), și atunci

\[ \bar{X}_n=\frac{1}{n} \sum_{i=n}^n X_i=\frac{1}{n} \sum_{i=n}^n\left(\mu+\sigma Z_i\right)=\mu+\sigma \bar{Z}_n \]

iar

\[ \begin{aligned} S_n^2 & =\frac{1}{n-1} \sum_{i=1}\left(X_i-\bar{X}_n\right)^2=\frac{1}{n-1} \sum_{i=1}\left(\mu+\sigma Z_i-\mu-\sigma \bar{Z}_n\right)^2 \\ & =\sigma^2 \frac{1}{n-1} \sum_{i=1}^n\left(Z_i-\bar{Z}_n\right)^2=\sigma^2 S_Z^2 \end{aligned} \]

Astfel, dacă arătăm că \(\bar{Z}_n\) și \(S_Z^2\) sunt independente atunci și \(\bar{X}_n\) și \(S_n^2\) sunt independente.

Pentru a demonstra independența dintre \(\bar{X}_n\) și \(S_n^2\) vom arăta pentru început că \(S_n^2=u\left(X_2-\bar{X}_n, \ldots X_n-\bar{X}_n\right)\) și apoi că \(\bar{X}_n\) este independent de \(\left(X_2-\bar{X}_n, \ldots X_n-\bar{X}_n\right)\). Pentru prima parte notăm că

\[ \begin{aligned} S_n^2 & =\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}_n\right)^2 \\ & =\frac{1}{n-1}\left[\sum_{i=2}^n\left(X_i-\bar{X}_n\right)^2+\left(X_1-\bar{X}_n\right)^2\right] \end{aligned} \]

și cum

\[ \bar{X}_n=\frac{1}{n} \sum_{i=1}^n X_i \Rightarrow n \bar{X}_n=\sum_{i=1}^n X_i \Rightarrow \sum_{i=1}^n\left(X_i-\bar{X}_n\right)=0 \Rightarrow X_1-\bar{X}_n = - \sum_{i=2}^n\left(X_i-\bar{X}_n\right) \]

de unde

\[ \begin{aligned} S_n^2 & =\frac{1}{n-1}\left[\sum_{i=2}^n\left(X_i-\bar{X}_n\right)^2+\left(\sum_{i=2}^n\left(X_i-\bar{X}_n\right)\right)^2\right] \\ & =u\left(X_2-\bar{X}_n, X_3-\bar{X}_n, \ldots X_n-\bar{X}_n\right) \end{aligned} \]

Pentru partea a doua vom calcula densitatea comună a vectorului \(\left(\bar{X}_n,X_2-\bar{X}_n, \ldots X_n-\bar{X}_n\right)\) și vom arăta că aceasta se poate factoriza¹. Știm că \(X_1,X_2,\ldots,X_n\sim\mathcal{N}(0,1)\), prin urmare densitatea vectorului \((X_1,X_2,\ldots,X_n)\) este

\[ \begin{aligned} f\left(x_1 \ldots x_n\right) & =f\left(x_1\right) \times \cdots f\left(x_n\right)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{x_1^2}{2}} \times \cdots \times \frac{1}{\sqrt{2 \pi}} e^{-\frac{x_n^2}{2}} \\ & =\left(\frac{1}{\sqrt{2 \pi}}\right)^n e^{-\frac{1}{2} \sum_{i=1}^n x_i^2} \end{aligned} \]

Considerăm transformarea \(g:\mathbb{R}^n \longrightarrow \mathbb{R}^n\) unde \(g\left(x_1, x_2, \ldots x_n\right) = \left(\bar{x}_n, x_2-\bar{x}_n, \ldots x_n-\bar{x}_n\right)\) și fie \(Y=g\left(X_1, X_2, \ldots X_n\right)\). Inversa se obține prin rezolvarea ecuației \(g(x)=y\) în \(x\)

\[ \left\{\begin{array}{l} y_1=\bar{x}_n \\ y_2=x_2-\bar{x}_n \\ \quad \quad \vdots\\ y_n=x_n-\bar{x}_n \end{array}\right. \]

care prin adunare conduce la \(\sum_{i=1}^n y_i=\sum_{j=2}^n x_j-(n-2) \bar{x}_n=2 \bar{x}_n-x_1\). Astfel găsim că \(x_1=2 y_1-\sum_{i=1}^n y_i=y_1-y_2 \cdots-y_n\) și \(x_i=y_i+\bar{x}_n=y_i+y_1\) pentru \(i\geq 2\), de unde inversa este

\[ g^{-1}(y_1,\ldots,y_n) = \left(y_1-y_2 \cdots-y_n, y_2+y_1, \ldots, y_n+y_1\right) \]

Matricea Jacobiană corespunzătoare lui \(g^{-1}\) este

\[ J_{g^{-1}} = \begin{pmatrix} 1 & -1 & -1 & \cdots & -1 \\ 1 & 1 & 0 & \cdots & 0 \\ 1 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ 1 & 0 & 0 & \cdots & 1 \end{pmatrix} \]

iar determinantul acesteia este \(\left|\det J_{g^{-1}}\right|=n\). Prin urmare, densitatea vectorului \(Y\) devine

\[ \begin{aligned} f_Y(y) &= f\left(g^{-1}(y)\right)\left|\det J_{g^{-1}}\right| \\ &= f\left(y_1-y_2 -\cdots -y_n, y_1+y_2, \ldots y_1+y_n\right) \times n \\ &= n \times\left(\frac{1}{\sqrt{2 \pi}}\right)^n e^{-\frac{1}{2}\left(y_1-y_2-\cdots-y_n\right)^2} \times e^{-\frac{1}{2} \sum_{i=2}^n\left(y_1+y_i\right)^2} \\ &=\left(\sqrt{\frac{n}{2 \pi}} e^{-\frac{n y_1^2}{2}}\right) \times\left(\frac{\sqrt{n}}{(\sqrt{2 \pi})^{n-1}} e^{-\frac{1}{2}\left[\sum_{i=2}^n y_i^2+\left(\sum_{i=2}^n y_i\right)^2\right]}\right) \\ &= h_1\left(y_1\right) \times h_2\left(y_2, \ldots y_n\right) \end{aligned} \]

ceea ce arată că \(\bar{X}_n\) este independent de \(\left(X_2-\bar{X}_n, \ldots X_n-\bar{X}_n\right)\).

3. Vom arăta că \((n-1)\frac{S_n^2}{\sigma^2}\sim\chi^2\left(n-1\right)\) prin inducție. Ca și la punctul anterior putem presupune, fără a pierde din generalitate, că \(X_i\sim\mathcal{N}(0,1)\) și în acest caz rămâne să verificăm că \((n-1)S_n^2\sim\chi^2\left(n-1\right)\).

Pentru început, să observăm că \((n-1) S_n^2=\sum_{i=1}^n\left(X_i-\bar{X}_n\right)^2\) și că

\[ \begin{aligned} X_i-\bar{X}_n & =X_i-\bar{X}_{n-1}+\bar{X}_{n-1}-\bar{X}_n \\ & =X_i-\bar{X}_{n-1}+\bar{X}_{n-1}-\frac{\sum_{i=1}^{n-1} X_i+X_n}{n} \\ & =X_i-\bar{X}_{n-1}+\bar{X}_{n-1}-\frac{(n-1) \bar{X}_{n-1}}{n}-\frac{X_n}{n} \\ & =X_i-\bar{X}_{n-1}+\frac{\bar{X}_{n-1}-X_n}{n} \end{aligned} \]

de unde

\[ \begin{aligned} (n-1) S_n^2= & \sum_{i=1}^n\left(X_i-\bar{X}_n\right)^2 \\ = & \sum_{i=1}^n\left(X_i-\bar{X}_{n-1}+\frac{\bar{X}_{n-1}-X_n}{n}\right)^2 \\ = & \sum_{i=1}^n\left[\left(X_i-\bar{X}_{n-1}\right)^2+2\left(X_i-\bar{X}_{n-1}\right) \frac{\left(\bar{X}_{n-1}-X_n\right)}{n}+\frac{\left(\bar{X}_{n-1}-X_n\right)^2}{n^2}\right] \\ = & \sum_{i=1}^{n}\left(X_i-\bar{X}_{n-1}\right)^2+\frac{2\left(\bar{X}_{n-1}-X_n\right)}{n} \sum_{i=1}^n\left(X_i-\bar{X}_{n-1}\right)+ \sum_{i=1}^{n}\frac{\left(\bar{X}_{n-1}-X_n\right)^2}{n^2}\\ = & \sum_{i=1}^{n-1}\left(X_i-\bar{X}_{n-1}\right)^2+\left(X_n-\bar{X}_{n-1}\right)^2+\frac{2\left(\bar{X}_{n-1}-X_n\right)}{n}\left(\sum_{i=1}^n X_i-n \bar{X}_{n-1}\right) \\ &+\frac{\left(\bar{X}_{n-1}-X_n\right)^2}{n} \\ = & (n-2)S_{n-1}^2+\left(X_n-\bar{X}_{n-1}\right)^2+\frac{2\left(\bar{X}_{n-1}-X_n\right)}{n}\left[(n-1)\bar{X}_{n-1} + X_n-n \bar{X}_{n-1}\right] \\ &+\frac{\left(\bar{X}_{n-1}-X_n\right)^2}{n} \\ = & (n-2) S_{n-1}^2+\left(\frac{n-1}{n}\right)\left(X_n-\bar{X}_{n-1}\right)^2 \end{aligned} \]

Astfel am obținut următoarea relație de recurență între \(S_n^2\) și \(S_{n-1}^2\):

\[ (n-1) S_n^2 = (n-2) S_{n-1}^2+\left(\frac{n-1}{n}\right)\left(X_n-\bar{X}_{n-1}\right)^2. \]

Dacă \(n=2\) atunci avem că \(S_2^2=\frac{1}{2}\left(X_2-X_1\right)^2\) și cum \(X_1,X_2\sim\mathcal{N}(0,1)\) independente deducem că \(X_1 - X_2\sim\mathcal{N}(0,2)\) prin urmare \(\left(\frac{X_1 - X_2}{\sqrt{2}}\right)^2\sim\chi^2(1)\), adică \(S_2^2\sim\chi^2(1)\). Presupunem afirmația adevărată pentru \(n\), i.e. \((n-1)S_n^2\sim\chi^2\left(n-1\right)\), și o vom arăta pentru \(n+1\):

\[ nS_{n+1}^2\sim\chi^2\left(n\right). \]

Din relația de recurență avem

\[ n S_{n+1}^2 = (n-1) S_{n}^2+\frac{n}{n+1}\left(X_{n+1}-\bar{X}_{n}\right)^2 \]

și cum din ipoteza de inducție \((n-1)S_n^2\sim\chi^2\left(n-1\right)\), este suficient să demonstrăm că \(\frac{n}{n+1}\left(X_{n+1}-\bar{X}_{n}\right)^2\sim\chi^2(1)\) și că \((n-1)S_n^2\) și \(\frac{n}{n+1}\left(X_{n+1}-\bar{X}_{n}\right)^2\) sunt independente. Am văzut din punctul b) că \(\bar{X}_n\) și \(S_n^2\) sunt independente și cum \(X_{n+1}\) este independent și de \(\bar{X}_n\) și de \(S_n^2\), deducem că \((n-1)S_n^2\) și \(\frac{n}{n+1}\left(X_{n+1}-\bar{X}_{n}\right)^2\) sunt independente (ca funcții de variabile aleatoare independente). În plus, \(X_{n+1}\sim\mathcal{N}(0,1)\) iar din punctul a) \(\bar{X}_n\sim\mathcal{N}\left(0, \frac{1}{n}\right)\) prin urmare, ținând cont de independența lor,

\[ X_{n+1}-\bar{X}_n \sim \mathcal{N}\left(0,1+\frac{1}{n}\right) \]

ceea ce implică

\[ \frac{X_{n+1}-\bar{X}_n}{\sqrt{\frac{n+1}{n}}} \sim \mathcal{N}(0,1) \Rightarrow\left(\frac{X_{n+1}-\bar{X}_n}{\sqrt{\frac{n+1}{n}}}\right)^2 \sim \chi^2(1). \]

Astfel, combinând cele două relații (împreună cu independența) găsim că

\[ n S_{n+1}^2 = \underbrace{(n-1) S_{n}^2}_{\sim\chi^2(n-1)}+\underbrace{\frac{n}{n+1}\left(X_{n+1}-\bar{X}_{n}\right)^2}_{\sim\chi^2(1)}\sim\chi^2(n). \]

Remarcă

În populații normale, cum \((n-1)\frac{S_n^2}{\sigma^2}\sim\chi^2\left(n-1\right)\) deducem că \(\operatorname{Var}\left((n-1)\frac{S_n^2}{\sigma^2}\right) = 2(n-1)\) de unde găsim că

\[ \operatorname{Var}\left(S_n^2\right)=\frac{2 \sigma^4}{n-1}. \]

Vom exemplifica rezultatul din Propoziția 2.4 plecând de la \(N=10000\) de eșantioane de volum \(n=20\) dintr-o populație \(\mathcal{N}(\mu,\sigma^2)\) cu \(\mu = 5\) și \(\sigma^2 = 3\). Următorul cod R ilustrează rezultatul:

set.seed(123)
N <- 10000

n <- 20
mu <- 5
sigma_sq <- 3

# generarea eșantioanelor
x <- matrix(rnorm(N * n, mean = mu, sd = sqrt(sigma_sq)), nrow = N, ncol = n)

# Media și varianța eșantioanelor
Xbar <- rowMeans(x)
S2 <- apply(x, 1, var)

Tstat <- (n - 1) * S2 / sigma_sq

# Ilustrare grafica
par(mfrow = c(1, 2))

hist(Xbar, freq = FALSE, breaks = 40, main = expression("Repartiția lui " * bar(X)[n]),
     xlab = "", 
     ylab = "Densitatea")
curve(dnorm(x, mean = mu, sd = sqrt(sigma_sq)/sqrt(n)), 
      col = 2, lwd = 2, add = TRUE)


hist(Tstat, freq = FALSE, breaks = 40,
     main = expression("Repartiția lui " * frac((n - 1) * S[n]^2, sigma^2)),
     xlab = "", 
     ylab = "Densitatea")

curve(dchisq(x, df = n - 1), col = 2, lwd = 2, add = TRUE)

Figura 2.1: Ilustrarea repartițiilor mediei și varianței eșantionului pentru populații normale: \(X_1,\ldots,X_{20}\sim\mathcal{N}(5,3)\)

Covarianța empirică

Fie \(X\) și \(Y\) două variabile aleatoare de medie \(\mu_{X}\) și \(\mu_{Y}\) și de varianțe \(\sigma_{X}^{2}\) respectiv \(\sigma_{Y}^{2}\). Ne interesăm la estimarea covarianței dintre cele două variabile

\[ \operatorname{Cov}(X,Y)=\mathbb{E}[(X-\mathbb{E}[X])(Y-\mathbb{E}[Y])]=\mathbb{E}[X Y]-\mathbb{E}[X] \mathbb{E}[Y] \]

Definiția 3.1 (Covarianța empirică și covarianța eșantionului) Fie \(\left(X_{1}, Y_{1}\right), \ldots,\left(X_{n}, Y_{n}\right)\) un eșantion de volum \(n\) de cupluri de variabile aleatoare independente și de repartiție comună dată de repartiția lui \((X, Y)\). Se numește covarianța empirică statistica \(C_{n}\) definită prin

\[ C_{n}=\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\bar{X}_{n}\right)\left(Y_{i}-\bar{Y}_{n}\right) \] și covarianța eșantionului statistica \(\hat{C}_n\) definită prin

\[ \hat{C}_{n}=\frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\bar{X}_{n}\right)\left(Y_{i}-\bar{Y}_{n}\right). \]

Covarianța empirică și a eșantionului verifică următoarele proprietăți:

Propoziția 3.1 (Proprietățile covarianței eșantionului) Fie \(\left(X_{1}, Y_{1}\right), \ldots,\left(X_{n}, Y_{n}\right)\) un eșantion de volum \(n\) de cupluri de variabile aleatoare independente și de repartiție comună dată de repartiția lui \((X, Y)\). Atunci

1. \(\mathbb{E}\left[C_n\right]=\frac{n-1}{n}\operatorname{Cov}(X,Y)\) și \(\mathbb{E}\left[\hat{C}_n\right]=\operatorname{Cov}(X,Y)\)
2. \(C_n \xrightarrow{\text { a.s }} \operatorname{Cov}(X,Y)\) și \(\hat{C}_n \xrightarrow{\text { a.s }} \operatorname{Cov}(X,Y)\)
3. În plus dacă \(\tau^{4}=\mathbb{E}\left[\left(X-\mu_{X}\right)^{2}\left(Y-\mu_{Y}\right)^{2}\right]<+\infty\), atunci \(\sqrt{n}\left(C_{n}-\operatorname{Cov}(X,Y)\right) \xrightarrow[n \rightarrow \infty]{d} \mathcal{N}\left(0, \tau^4 - \operatorname{Cov}(X,Y)^2\right)\) și respectiv \(\sqrt{n}\left(\hat{C}_{n}-\operatorname{Cov}(X,Y)\right) \xrightarrow[n \rightarrow \infty]{d} \mathcal{N}\left(0, \tau^4 - \operatorname{Cov}(X,Y)^2\right)\)

Demonstrație. Avem

1. Adunând și scăzând \(\mu_{X}\) și \(\mu_{Y}\) obținem

\[ \begin{aligned} & \sum_{j=1}^{n}\left(X_{j}-\bar{X}_{n}\right)\left(Y_{j}-\bar{Y}_{n}\right)=\sum_{j=1}^{n}\left(\left(X_{j}-\mu_{X}\right)+\left(\mu_X-\bar{X}_{n}\right)\right)\left(\left(Y_{j}-\mu_{Y}\right)+\left(\mu_Y-\bar{Y}_{n}\right)\right) \\ & =\sum_{i=1}^{n}\left(X_{i}-\mu_{X}\right)\left(Y_{i}-\mu_{Y}\right)+\sum_{i=1}^{n}\left(X_{i}-\mu_{X}\right)\left(\mu_{Y}-\bar{Y}_{n}\right)+\sum_{i=1}^{n}\left(\mu_{X}-\bar{X}_{n}\right)\left(Y_{i}-\mu_{Y}\right)+ \\ &\quad +\sum_{i=1}^{n}\left(\mu_{X}-\bar{X}_{n}\right)\left(\mu_{Y}-\bar{Y}_{n}\right) \\ & =\sum_{i=1}^{n}\left(X_{i}-\mu_{X}\right)\left(Y_{i}-\mu_{Y}\right)+\left(\mu_{Y}-\bar{Y}_{n}\right) \sum_{i=1}^{n}\left(X_{i}-\mu_{X}\right)+\left(\mu_{X}-\bar{X}_{n}\right) \sum_{i=1}^{n}\left(Y_{i}-\mu_{Y}\right)+\\ & \quad + n\left(\mu_{X}-\bar{X}_{n}\right)\left(\mu_{Y}-\bar{Y}_{n}\right) \\ & =\sum_{i=1}^{n}\left(X_{i}-\mu_{X}\right)\left(Y_{i}-\mu_{Y}\right)+n\left(\mu_{Y}-\bar{Y}_{n}\right)\left(\bar{X}_{n}-\mu_{X}\right)+n\left(\mu_{X}-\bar{X}_{n}\right)\left(\bar{Y}_{n}-\mu_{Y}\right)+\\ &\quad +n\left(\mu_{X}-\bar{X}_{n}\right)\left(\mu_{Y}-\bar{Y}_{n}\right) \\ & =\sum_{i=1}^{n}\left(X_{i}-\mu_{X}\right)\left(Y_{i}-\mu_{Y}\right)-n\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right) . \end{aligned} \]

De asemenea putem scrie

\[ \begin{aligned} n^{2}\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right) & =\left(\sum_{i=1}^{n}\left(X_{i}-\mu_{X}\right)\right)\left(\sum_{i=1}^{n}\left(Y_{i}-\mu_{Y}\right)\right) \\ & =\sum_{i=1}^{n}\left(X_{j}-\mu_{X}\right)\left(Y_{n}-\mu_{Y}\right)+\sum_{i \neq j}\left(X_{i}-\mu_{X}\right)\left(Y_{j}-\mu_{Y}\right) \end{aligned} \]

Din liniaritatea mediei avem

\[ \begin{aligned} \mathbb{E}\left[C_{n}\right] & =\mathbb{E}\left[\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu_{X}\right)\left(Y_{i}-\mu_{Y}\right)-\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right)\right] \\ & =\frac{1}{n} \sum_{i=1}^{n} \mathbb{E}\left[\left(X_{i}-\mu_{X}\right)\left(Y_{i}-\mu_{Y}\right)\right]-\mathbb{E}\left[\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right)\right] \\ & =\frac{1}{n} \sum_{i=1}^{n} \operatorname{Cov}(X,Y)-\frac{1}{n^{2}} \mathbb{E}\left[n^{2}\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right)\right] \end{aligned} \]

Ținând cont de descompunerea anterioară și de independența cuplurilor \((X_{i}, Y_{i})\) găsim

\[ \begin{aligned} \mathbb{E}\left[n^{2}\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right)\right] & =\mathbb{E}\left[\sum_{i=1}^{n}\left(X_{j}-\mu_{X}\right)\left(Y_{j}-\mu_{Y}\right)+\sum_{i \neq j}\left(X_{i}-\mu_{X}\right)\left(Y_{j}-\mu_{Y}\right)\right] \\ & =\sum_{i=1}^{n} \mathbb{E}\left[\left(X_{j}-\mu_{X}\right)\left(Y_{j}-\mu_{Y}\right)\right]+\sum_{i \neq j} \mathbb{E}\left[\left(X_{i}-\mu_{X}\right)\left(Y_{j}-\mu_{Y}\right)\right] \\ & =\sum_{i=1}^{n} \operatorname{Cov}(X,Y)+\sum_{i \neq j} \underbrace{\operatorname{Cov}\left(X_{i}, Y_{j}\right)}_{=0} \\ & =n \operatorname{Cov}(X,Y). \end{aligned} \]

Astfel, deducem că

\[ \mathbb{E}\left[C_{n}\right]=\frac{n-1}{n} \operatorname{Cov}(X,Y). \]

Ținând cont de definiția lui \(\hat{C}_{n}\), estimatorul

\[ \hat{C}_{n}=\frac{n}{n-1} C_{n} = \frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\bar{X}_{n}\right)\left(Y_{i}-\bar{Y}_{n}\right) \]

verifică \(\mathbb{E}\left[\hat{C}_{n}\right]=\operatorname{Cov}(X,Y)\).

2. Putem scrie

\[ C_{n}=\frac{1}{n} \sum_{i=1}^{n} Z_{i}-\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right) \]

Din Legea Numerelor Mari, primul termen converge aproape sigur la \(\operatorname{Cov}(X,Y)\) pe când al doilea termen converge aproape sigur la \(0\) (deoarece \(\bar{X}_{n}\) și \(\bar{Y}_{n}\) converg aproape sigur la \(\mu_{X}\) și respectiv \(\mu_{Y}\)). Astfel,

\[ C_n \xrightarrow{\text { a.s }} \operatorname{Cov}(X,Y) \]

și cum \(\frac{n-1}{n}\to 1\) deducem că \(\hat{C}_n \xrightarrow{\text { a.s }} \operatorname{Cov}(X,Y)\).

3. Pentru început vom arăta că

\[ \sqrt{n}\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right) \xrightarrow[n \rightarrow+\infty]{\mathbb{P}} 0 \]

Cum pentru toate constantele pozitive \(a, b\), are loc inegalitatea \(2a b \leq a^{2}+ b^{2}\), obținem că

\[ \mathbb{E}\left[\sqrt{n}\left|\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right)\right|\right] \leq \sqrt{n} \frac{1}{2} \mathbb{E}\left[\left(\bar{X}_{n}-\mu_{X}\right)^{2}\right]+\sqrt{n} \frac{1}{2} \mathbb{E}\left[\left(\bar{Y}_{n}-\mu_{Y}\right)^{2}\right]=\frac{\sigma_{X}^{2}}{2 \sqrt{n}}+\frac{\sigma_{Y}^{2}}{2 \sqrt{n}} \] Aplicând inegalitatea lui Markov, pentru \(\epsilon>0\),

\[ \begin{aligned} \mathbb{P}\left[\sqrt{n}\left|\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right)\right| \geq \epsilon\right] & \leq \frac{1}{\epsilon} \mathbb{E}\left[\sqrt{n}\left|\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right)\right|\right] \\ & \leq \frac{\sigma_{X}^{2}}{2 \sqrt{n} \epsilon}+\frac{\sigma_{Y}^{2}}{2 \sqrt{n} \epsilon} \end{aligned} \]

de unde concluzia.

Alternativ, aplicând inegalitatea Cauchy-Schwarz, avem

\[ \begin{aligned} \mathbb{E}\left[\sqrt{n}\left|\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right)\right|\right] & \leq \sqrt{n} \sqrt{\mathbb{E}\left[\left|\bar{X}_{n}-\mu_{X}\right|^{2}\right]} \sqrt{\mathbb{E}\left[\left|\bar{Y}_{n}-\mu_{Y}\right|^{2}\right]} \\ & =\sqrt{n} \frac{\sigma_{X} \sigma_{Y}}{n} \end{aligned} \]

O a treia soluție presupune aplicarea Teoremei lui Slutsky pentru că

\[ \sqrt{n}\left(\bar{X}_{n}-\mu_{X}\right) \xrightarrow[n \rightarrow \infty]{d} \mathcal{N}\left(0, \sigma_{X}^{2}\right) \quad \text { și } \quad \bar{Y}_{n}-\mu_{Y} \xrightarrow[n \rightarrow \infty]{\mathbb{P}} 0, \]

implică convergența în repartiție la \(0\) prin urmare și convergența în probabilitate.

Acum, am văzut că

\[ C_{n}=\frac{1}{n} \sum_{i=1}^{n} Z_{i}-\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right) \]

de unde

\[ \begin{aligned} \sqrt{n}\left(C_{n}-\operatorname{Cov}(X,Y)\right) &= \sqrt{n}\left[\bar{Z}_n - \operatorname{Cov}(X,Y) - \left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right) \right]\\ &= \sqrt{n}\left(\bar{Z}_n - \operatorname{Cov}(X,Y)\right) + \sqrt{n}\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right) \end{aligned} \]

și cum din Teorema Limită Centrală avem că

\[ \sqrt{n}\left(\bar{Z}_n - \operatorname{Cov}(X,Y)\right) \xrightarrow[n \rightarrow \infty]{d} \mathcal{N}\left(0, \operatorname{Var}(Z_1)\right) \]

unde \(\operatorname{Var}(Z_1) = \tau^4 - \operatorname{Cov}(X,Y)^2\), și cum am arătat anterior că

\[ \sqrt{n}\left(\bar{X}_{n}-\mu_{X}\right)\left(\bar{Y}_{n}-\mu_{Y}\right) \xrightarrow[n \rightarrow+\infty]{\mathbb{P}} 0 \]

aplicând Teorema lui Slutsky deducem că

\[ \sqrt{n}\left(C_{n}-\operatorname{Cov}(X,Y)\right) \xrightarrow[n \rightarrow \infty]{d} \mathcal{N}\left(0, \tau^4 - \operatorname{Cov}(X,Y)^2\right). \]

Coeficientul de asimetrie și de aplatizare

Coeficientul de asimetrie (skewness) este o măsură a simetriei (sau mai bine a lipsei simetriei) unei repartiții. Fiind dată o variabilă aleatoare \(X\) cu \(\mathbb{E}[|X|^3]<\infty\), \(\mathbb{E}[X]=\mu\) și \(Var(X)=\sigma^2>0\) coeficientul de asimetrie este definit prin relația

\[ \gamma_1(X) = \mathbb{E}\left[\frac{(X-\mu)^3}{\sigma^3}\right]. \]

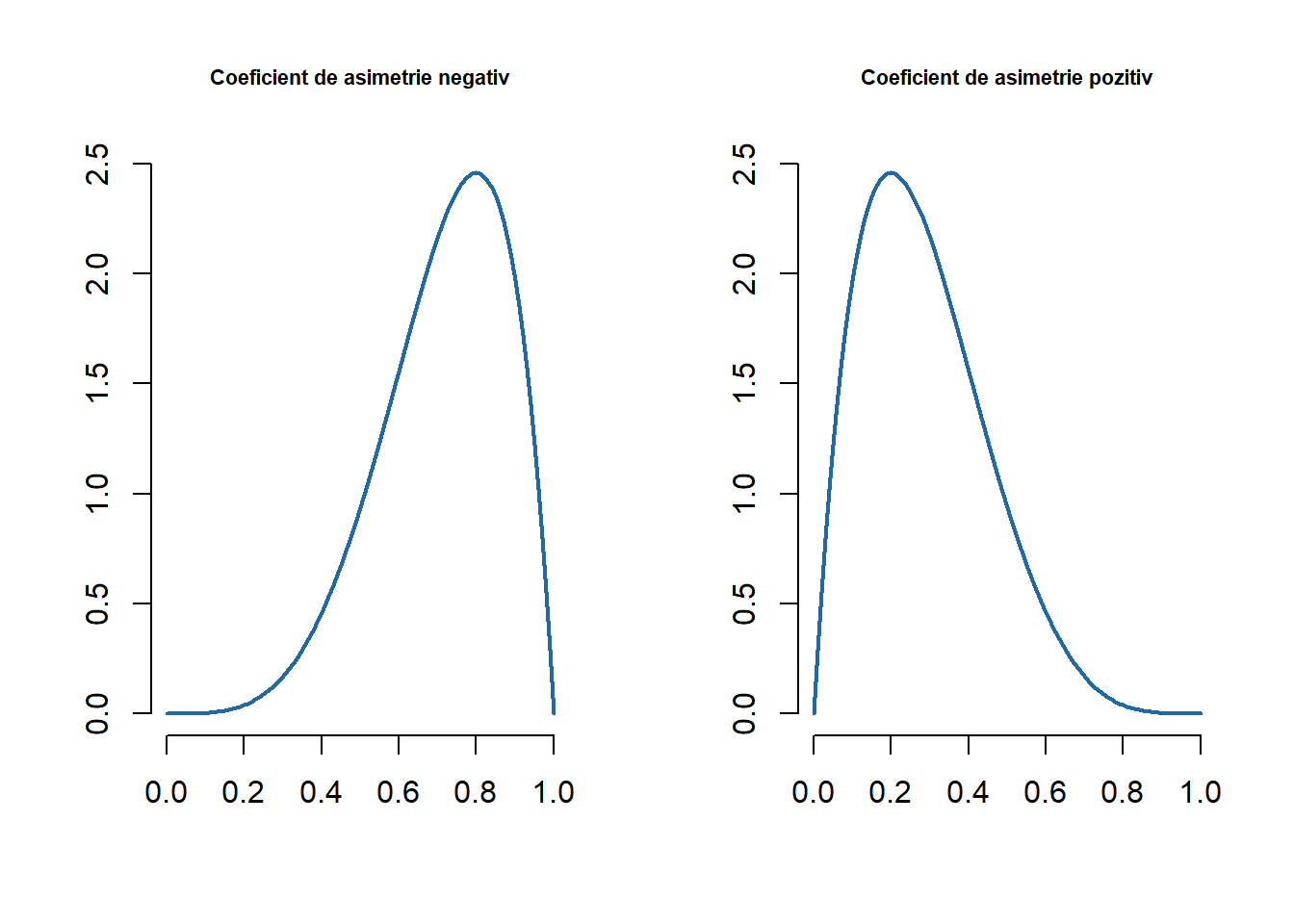
Cum repartiția normală este simetrică față de media sa \(\mu\) atunci coeficientul de asimetrie este 0. În general o repartiție unimodală are coeficientul de asimetrie negativ dacă are o coadă mai lungă spre stânga (masa este concentrată mai spre dreapta) și pozitiv dacă are coada mai lungă spre dreapta (masa este concentrată mai spre stânga).

par(mfrow = c(1,2))

curve(dbeta(x, 5, 2), 
      main = "Coeficient de asimetrie negativ", 
      col = myblue, 
      lwd = 2, 
      bty = "n",
      xlab = "",
      ylab = "",
      cex.main = 0.7)

curve(dbeta(x, 2, 5), 
      main = "Coeficient de asimetrie pozitiv", 
      col = myblue, 
      lwd = 2, 
      bty = "n",
      xlab = "",
      ylab = "",
      cex.main = 0.7)

Figura 4.1: Ilustrarea unor densități cu coeficientul de asimetrie negativ, respectiv pozitiv.

Coeficientul de asimetrie pentru un eșantion \(X_1, X_2, \ldots, X_n\) de volum \(n\) este

\[ b_1 = \frac{\frac{1}{n}\sum_{i = 1}^{n} (X_i - \bar{X}_n)^3}{\left(\frac{1}{n}\sum_{i = 1}^{n} (X_i - \bar{X}_n)^2\right)^{\frac{3}{2}}}. \]

Coeficientul de aplatizare (kurtosis) măsoară dacă datele au coadă mai lungă sau mai scurtă în raport cu repartiția normală. Fiind dată o variabilă aleatoare \(X\) cu \(\mathbb{E}[X^4]<\infty\), \(\mathbb{E}[X]=\mu\) și \(Var(X)=\sigma^2>0\) coeficientul de aplatizare este definit prin relația

\[ \gamma_2(X) = \mathbb{E}\left[\frac{(X-\mu)^4}{\sigma^4}\right] - 3. \]

Pentru o variabilă aleatoare repartizată normal, \(Z\sim \mathcal{N}(\mu, \sigma^2)\), avem că \(\gamma_2(Z) = 0\).

Coeficientul de aplatizare pentru un eșantion \(X_1, X_2, \ldots, X_n\) este

\[ b_2 = \frac{\frac{1}{n}\sum_{i = 1}^{n} (X_i - \bar{X}_n)^4}{\left(\frac{1}{n}\sum_{i = 1}^{n} (X_i - \bar{X}_n)^2\right)^{2}} - 3. \]

Articolul (Gill 1998) prezintă diferite metode de calcul pentru coeficientul de aplatizare și cel de asimetrie într-un eșantion.

Exercițiul 4.1 Construiți în R două funcții, skewness_coef() și kurtosis_coef(), care să permită calculul coeficientului de asimetrie și respectiv a coeficientului de aplatizare pentru un eșantion dat.

Soluție. Următorul cod implementează cele două funcții din cerință:

skewness_coef <- function(x){
  n <- length(x)
  x <- x - mean(x)
  y <- sqrt(n) * sum(x^3)/(sum(x^2)^(3/2))
  return(y)
}

kurtosis_coef <- function(x){
  n <- length(x)
  x <- x - mean(x)
  r <- n * sum(x^4)/(sum(x^2)^2)
  y <- r-3
  return(y)
}

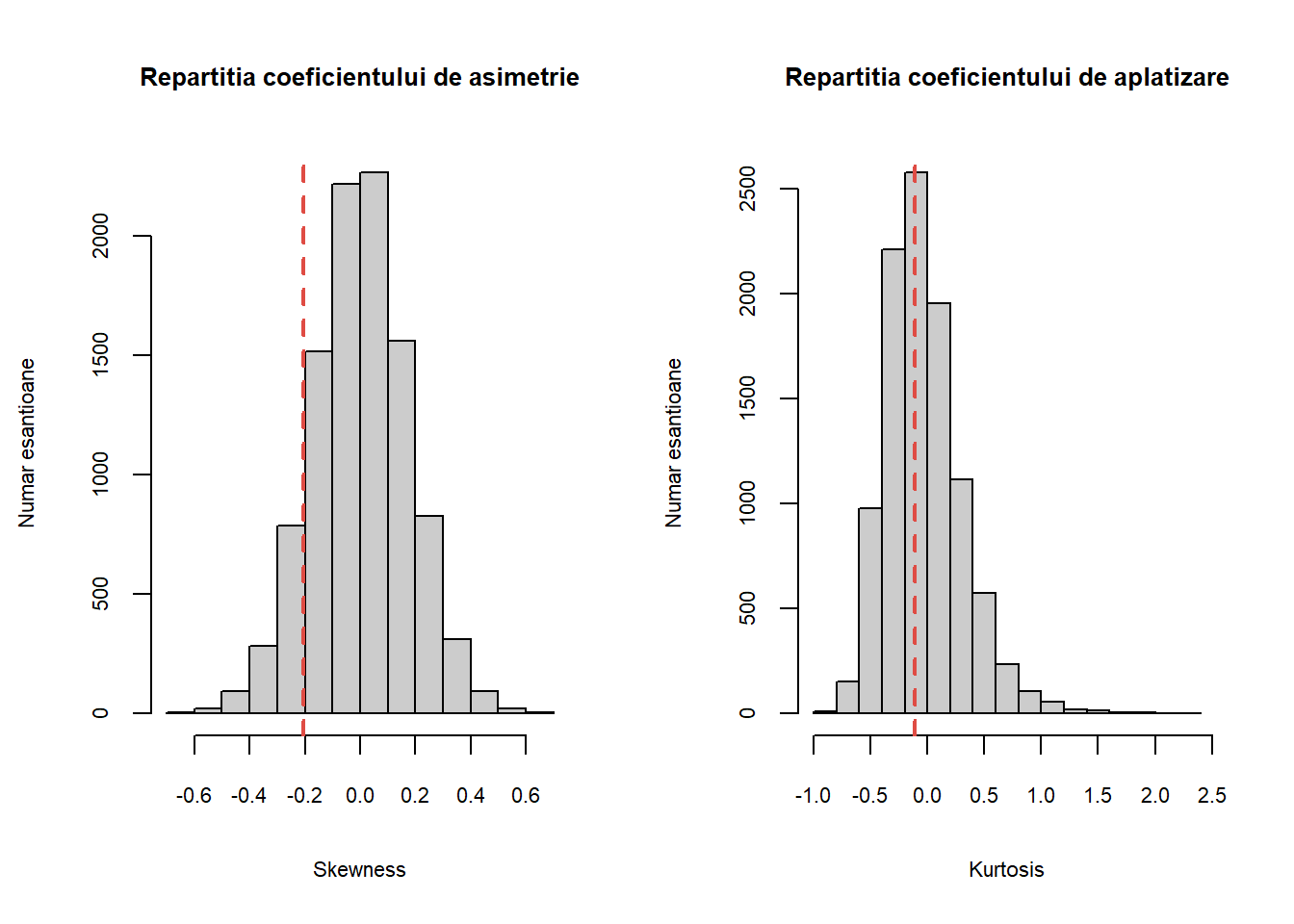
Deplasarea față de valoarea \(0\), atât pentru coeficientul de asimetrie cât și pentru cel de aplatizare indică o deplasare față de repartiția normală. Pentru a decide dacă o anumită deplasare față de \(0\) este mare sau mică se poate folosi un studiu de simulare. De exemplu, coeficientul de asimetrie calculat pentru greutatea la naștere a celor 189 de copii din setul de date birthwt (din pachetul MASS) este -0.207 iar coeficientul de aplatizare este -0.113. Pentru a vedea dacă -0.207 și respectiv dacă -0.113 sunt valori tipice pentru coeficientul de asimetrie și respectiv de aplatizare dintr-un eșantion de 189 de observații dintr-o populație normală, repetăm următorul proces de un număr mare de ori (de exemplu \(10000\)): generăm aleator 189 de observații dintr-o repartiție normală și calculăm cei doi coeficienți.

Următorul cod R ilustrează acest proces:

library(MASS)
weight <- birthwt$bwt

n_wt <- length(weight)
m_wt <- mean(weight)
sd_wt <- sd(weight)

skew_bwt <- skewness_coef(weight)
kurt_bwt <- kurtosis_coef(weight)

# functia de simulare
skew_kurt_sim <- function(fun = function(n) rnorm(n), n = 100){
  x <- fun(n)
  kurt <- kurtosis_coef(x)
  skew <- skewness_coef(x)
  
  return(c(kurtosis = kurt, skewness = skew))
}

# replicam de 10000 de ori procesul 
out1 <- replicate(10000, 
         skew_kurt_sim(fun = function(n) rnorm(n), 
                       n = n_wt))

Figurile de mai jos reprezintă histogramele a \(10000\) de valori ale coeficientului de asimetrie și respectiv de aplatizare, calculate pentru \(10000\) de eșantioane de talie 189 dintr-o repartiție normală standard.

# ilustram grafic
par(mfrow = c(1,2))

hist(out1[2,],
     col = "grey80",
     main = "Repartitia coeficientului de asimetrie",
     xlab = "Skewness",
     ylab = "Numar esantioane",
     cex.main = 0.8,
     cex.axis = 0.7,
     cex.lab = 0.7)
abline(v = skew_bwt, col = myred, 
       lty = 2, lwd = 2)

hist(out1[1,],
     col = "grey80",
     main = "Repartitia coeficientului de aplatizare",
     xlab = "Kurtosis",
     ylab = "Numar esantioane",
     cex.main = 0.8,
     cex.axis = 0.7,
     cex.lab = 0.7)
abline(v = kurt_bwt, col = myred, 
       lty = 2, lwd = 2)

Figura 4.2: Repartiția coeficientului de asimetrie și de aplatizare pentru exemplul considerat.

Statistici de ordine

În cele ce urmează vom introduce noțiunea de statistică de ordine:

Definiția 5.1 (Statistică de ordin \(k\)) Fie \(X_1,X_2,\ldots,X_n\) un eșantion de volum \(n\) dintr-o populație a cărei funcție de repartiție este \(F\) și \(h_k:\mathbb{R}^n\mapsto\mathbb{R}\) o funcție care face să-i corespundă vectorului \((x_1,\ldots,x_n)\) a \(k\)-a cea mai mică valoare dintre \(x_1,\ldots, x_n\). Se numește statistică de ordin \(k\), și se notează cu \(X_{(k)}\), statistica

\[ X_{(k)} = h_k(X_1,\ldots, X_n). \]

Conform definiției de mai sus avem că

\[ \begin{aligned} X_{(1)} &= \min\{X_1,\ldots, X_n\}\\ X_{(n)} &= \max\{X_1,\ldots, X_n\}. \end{aligned} \]

Se poate verifica cu ușurință că statistica de ordin \(k\) verifică următoarele proprietăți:

Propoziția 5.1 (Funcția de repartiție și densitatea statisticii de ordin \(k\)) Fie \(X_1,X_2,\ldots,X_n\) un eșantion de volum \(n\) dintr-o populație a cărei funcție de repartiție este \(F\) și densitate de repartiție este \(f\). Atunci

1. Funcția de repartiție a statisticii de ordin \(k\), i.e. \(X_{(k)}\) este \[ F_{X_{(k)}}(x) = \sum_{j=k}^{n}\binom{n}{j}F(x)^j(1-F(x))^{n-j} \]

2. Densitatea de repartiție a statisticii de ordin \(k\), i.e. \(X_{(k)}\) este \[ f_{X_{(k)}} = k\binom{n}{k}f(x)F(x)^{k-1}(1-F(x))^{n-k}. \]

Demonstrație. Pentru primul punct avem:

1. Fie \(x\in\mathbb{R}\) fixat și fie \(Y\) variabila aleatoare care ne dă numărul de variabile \(X_1,X_2,\ldots,X_n\) care sunt mai mici sau egale cu \(x\), i. e.

\[ Y = \mathbf{1}_{\{X_1\leq x\}} + \mathbf{1}_{\{X_2\leq x\}} + \cdots + \mathbf{1}_{\{X_n\leq x\}} = \sum_{i = 1}^{n}\mathbf{1}_{\{X_i\leq x\}}. \]

Variabilele aleatoare \(\mathbf{1}_{\{X_i\leq x\}}\) sunt variabile de tip Bernoulli \(\mathcal{B}(p)\) unde \(p=\mathbb{P}(X_i\leq x) = F(x)\) și cum \(X_1,X_2,\ldots,X_n\) sunt independente deducem că \(\mathbf{1}_{\{X_1\leq x\}}, \mathbf{1}_{\{X_2\leq x\}}, \ldots, \mathbf{1}_{\{X_n\leq x\}}\) sunt independente iar \(Y\sim \mathrm{Bin}(n,F(x))\), ca sumă de Bernoulli independente.

Observăm că între statistica de ordin \(k\), \(X_{(k)}\), și \(Y\) avem relația

\[ \mathbb{P}(X_{(k)}\leq x) = \mathbb{P}(Y \geq k) \]

ceea ce conduce la

\[ \begin{aligned} F_{X_{(k)}}(x) &= \mathbb{P}(X_{(k)}\leq x) = \sum_{j=k}^{n}\mathbb{P}(Y = j)\\ &= \sum_{j=k}^{n}\binom{n}{j}F(x)^j(1-F(x))^{n-j}. \end{aligned} \]

2. Pentru a determina densitatea, calculăm derivata funcției de repartiție și avem \(f_{X_{(k)}}(x)=\)

\[ \begin{aligned} f_{x_{(k)}}(x) & = \frac{d}{d x} F_{(k)}(x) = \frac{d}{d x} \sum_{j=k}^n\binom{n}{j} F(x)^j(1-F(x))^{n-j} \\ &= \sum_{j=k}^n\binom{n}{j} \frac{d}{d x}\left[F(x)^j(1-F(x))^{n-j}\right]\\ &= \sum_{j=k}^n\binom{n}{j}\left[j F(x)^{j-1} f(x)(1-F(x))^{n-j} - (n-j) F(x)^{j}(1-F(x))^{n-j-1}f(x) \right]\\ &= k\binom{n}{k}f(x)F(x)^{k-1}(1-F(x))^{n-k} + \underbrace{\sum_{j=k+1}^n\binom{n}{j}j F(x)^{j-1} f(x)(1-F(x))^{n-j}}_{T_1} - \\ &\quad - \underbrace{\sum_{j=k}^{n-1}\binom{n}{j}(n-j) F(x)^{j} f(x)(1-F(x))^{n-j-1}}_{T_2} \end{aligned} \]

Cum

\[ T_1 - T_2 = \sum_{l=k}^{n-1}\binom{n}{l+1}(l+1) F(x)^{l} f(x)(1-F(x))^{n-l-1} - \sum_{j=k}^{n-1}\binom{n}{j}(n-j) F(x)^{j} f(x)(1-F(x))^{n-j-1} \]

și \(\binom{n}{l+1}(l+1) = \binom{n}{j}(n-j)\) găsim că \(T_1 = T_2\), prin urmare

\[ f_{X_{(k)}}(x) = k\binom{n}{k}f(x)F(x)^{k-1}(1-F(x))^{n-k}. \]

Remarcă

Expresia densității de repartiție a statisticii de ordin \(k\) se poate reține și dacă apelăm la următorul argument euristic bazat pe repartiția multinomială (generalizarea repartiției binomiale). Pentru ca statistica de ordin \(k\), \(X_{(k)}\), să fie aproape de \(x\) (așa încât să aproximăm probabilitatea cu densitatea ori unitatea de lungime) ar trebui ca \(k-1\) dintre variabile să fie mai mici decât \(x\), o variabilă să fie aproape \(x\) și \(n - k\) să fie mai mari decât \(x\). Categoriile și probabilitățile lor sunt date mai jos

\[ \begin{array}{cccc} \hline \text { Categoria} & \text { Descriere } & \text { Probabilitatea } & \text { \# Observații} \\ \hline 1 & \text { Mai mic decât } x & p_1=\mathbb{P}(X<x)=F(x) & k-1 \\ 2 & \text { Aproape egal cu } x & p_2=\mathbb{P}(x\leq X\leq x+dx)\approx f(x)dx & 1 \\ 3 & \text { Mai mare decât } x & p_3=\mathbb{P}(X>x)=1-F(x) & n-k \\ \hline \end{array} \]

prin urmare, prin aplicarea repartiției multinomiale cu trei categorii găsim

\[ \begin{aligned} & P\left(x \leq X_{(k)} \leq x+d x\right) \approx f_{X_{(k)}}(x) dx \\ & \approx P[(k-1) \text { din categoria } 1,1 \text { din categoria } 2,(n-k) \text { din categoria } 3] \\ & \approx \binom{n}{k-1, 1 ,n-k} p_1^{k-1} p_2^1 p_3^{n-k} \\ & \approx \frac{n !}{(k-1) ! 1 !(n-k) !}\left\{\left[F\left(x\right)\right]^{k-1} f\left(x\right) d x\left[1-F\left(x\right)\right]^{n-k}\right\} \\ & \end{aligned} \]

iar densitatea căutată este

\[ f_{X_{(k)}}(x) = \frac{n !}{(k-1) !(n-k) !}\left[F(x)\right]^{k-1} f(x)\left[1-F(x)\right]^{n-k} \]

Scopul următorului exercițiu este de a ilustra empiric proprietățile statisticii de ordin \(k\) prezentate în Propoziția 5.1.

Exercițiul 5.1 Fie \(X_1,X_2,\ldots,X_n\) un eșantion de volum \(n=100\) din repartiția \(\mathrm{Exp}(\lambda)\).

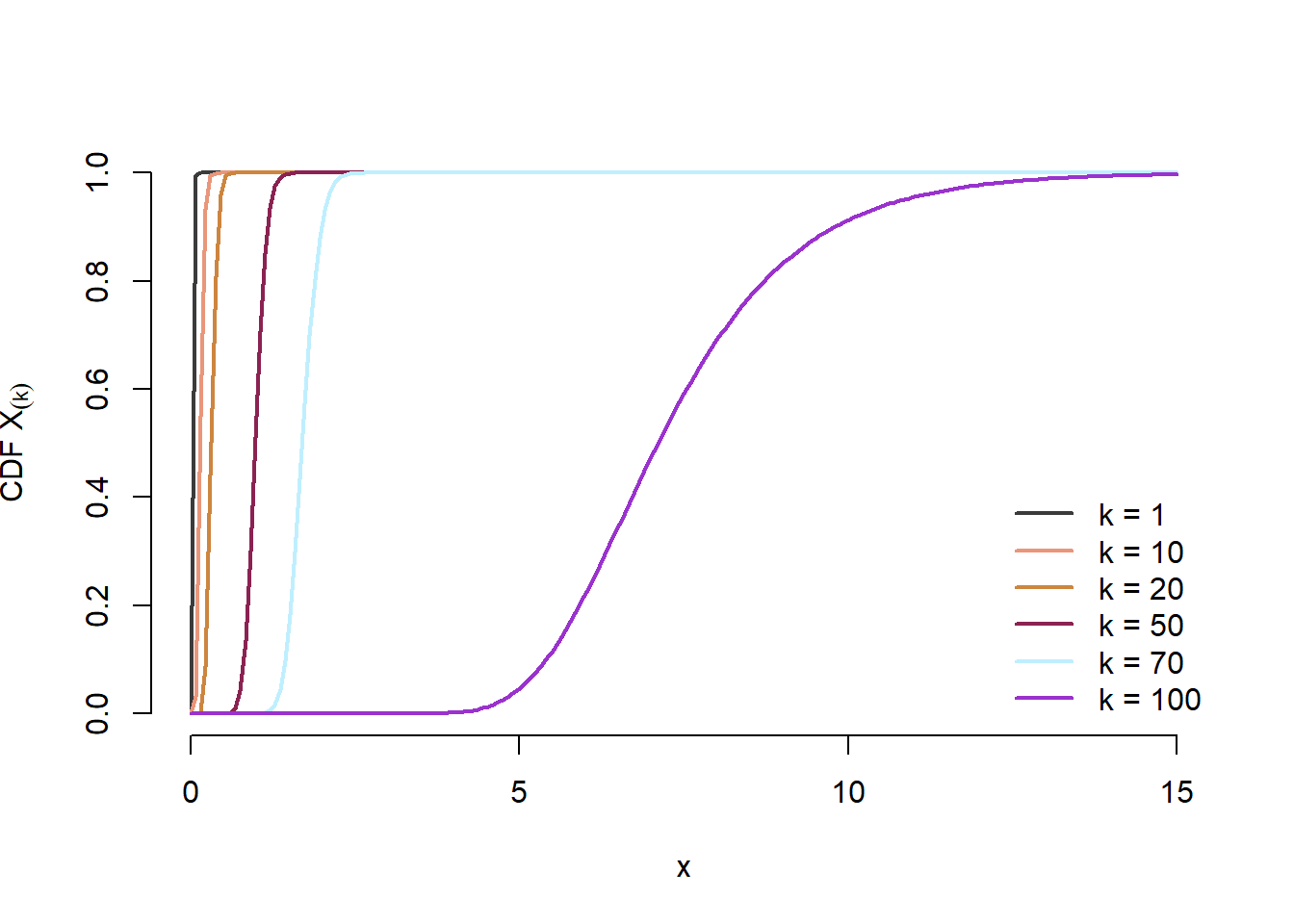
1. Implementați în R câte o funcție care să permită calculul funcției de repartiție, respectiv a densității statisticii de ordin \(k\).

2. Pentru \(\lambda = 0.7\), ilustrați pe același grafic funcțiile de repartiție corespunzătoare statisticii de ordin \(k\) pentru \(k\in\{1, 10, 20, 50, 70, 100\}\). Aceeași cerință pentru densitățile de repartiție.

3. Generați \(N = 10000\) de eșantioane de volum \(n=100\) din \(\mathrm{Exp}(0.7)\), calculați statisticile de ordin \(k\in\{1, 10, 20, 50, 70, 100\}\) și comparați grafic (prin intermediul unei histograme) repartiția empirică cu cea teoretică.

Soluție. Avem

1. Următoarele două funcții implementează expresiile funcției de repartiție, respectiv a densității de repartiție pentru statistica de ordin \(k\) conform relațiilor din Propoziția 5.1:

# Functia de repartitie a statisticii de ordin k
cdf_stat_ord_k <- function(x, n = 1, k = 1, lambda = 1){
     if (k > n){
          stop("Ordinul trebuie sa fie mai mic decat volumul esantionului!")
     }
     
     ind <- k:n
     cdf_exp <- pexp(x, lambda)^ind*pexp(x, lambda, lower.tail = FALSE)^(n-ind)
     comb <- choose(n, ind)
     
     out <- sum(comb*cdf_exp)
     
     return(out)
}

cdf_stat_ord_k <- Vectorize(cdf_stat_ord_k, vectorize.args = "x")


# Densitatea statisticii de ordin k
dens_stat_ord_k <- function(x, n = 1, k = 1, lambda = 1){
     if (k > n){
          stop("Ordinul trebuie sa fie mai mic decat volumul esantionului!")
     }
     
     out <- k*choose(n, k) * dexp(x, lambda) * pexp(x, lambda)^(k-1)*(1 - pexp(x, lambda))^(n - k)
  
  return(out)
}

2. În Figura 5.1 sunt prezentate funcțiile de repartiție \(F_{X_{(k)}}(x)\) pentru \(k\in\{1, 10, 20, 50, 70, 100\}\):

n <- 100
lambda0 <- 0.7

t <- seq(0, 15, length.out = 200)
ords <- c(1, 10, 20, 50, 70, n)


plot(t, 
     cdf_stat_ord_k(t, n, ords[1], lambda = lambda0), 
     type = "n", 
     xlab = "x", 
     ylab = expression(paste("CDF ", X[(k)])),
     bty = "n",
     lwd = 3)

set.seed(1234)
cols <- colors()[sample(1:657, length(ords))]

for (i in seq_along(ords)){
  k <- ords[i]
  
  lines(t, 
        cdf_stat_ord_k(t, n, k, lambda = lambda0),
        lwd = 2,
        col = cols[i])
}

legend("bottomright", 
       legend = paste0("k = ", ords), 
       col = cols, 
       lwd = 2, 
       bty = "n")

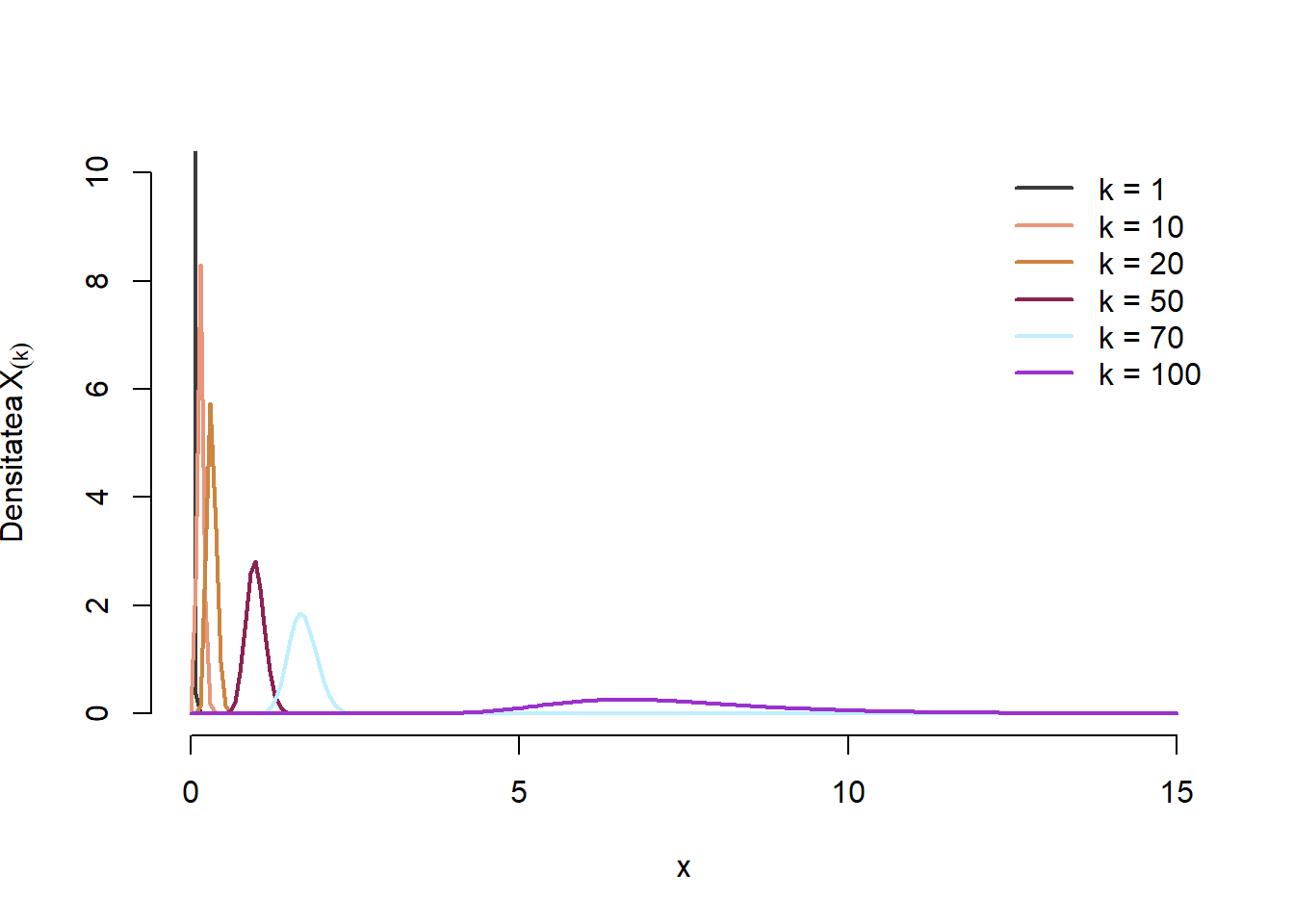
Figura 5.1: Ilustrarea funcțiilor de repartiție ale statisticilor de ordin \(k\), pentru \(k\in\{1, 10, 20, 50, 70, 100\}\) în cazul \(\mathrm{Exp}(0.7)\)

Densitățile de repartiție \(f_{X_{(k)}}(x)\) ale statisticii de ordin \(k\) pentru \(k\in\{1, 10, 20, 50, 70, 100\}\) sunt ilustrate mai jos:

n <- 100
lambda0 <- 0.7

t <- seq(0, 15, length.out = 200)
ords <- c(1, 10, 20, 50, 70, n)


plot(t, 
     dens_stat_ord_k(t, n, ords[1], lambda = lambda0), 
     type = "n", 
     xlab = "x", 
     ylab = expression(paste("Densitatea ", X[(k)])),
     ylim = c(0, 10),
     bty = "n",
     lwd = 3)

set.seed(1234)
cols <- colors()[sample(1:657, length(ords))]

for (i in seq_along(ords)){
  k <- ords[i]
  
  lines(t, 
        dens_stat_ord_k(t, n, k, lambda = lambda0),
        lwd = 2,
        col = cols[i])
}

legend("topright", 
       legend = paste0("k = ", ords), 
       col = cols, 
       lwd = 2, 
       bty = "n")

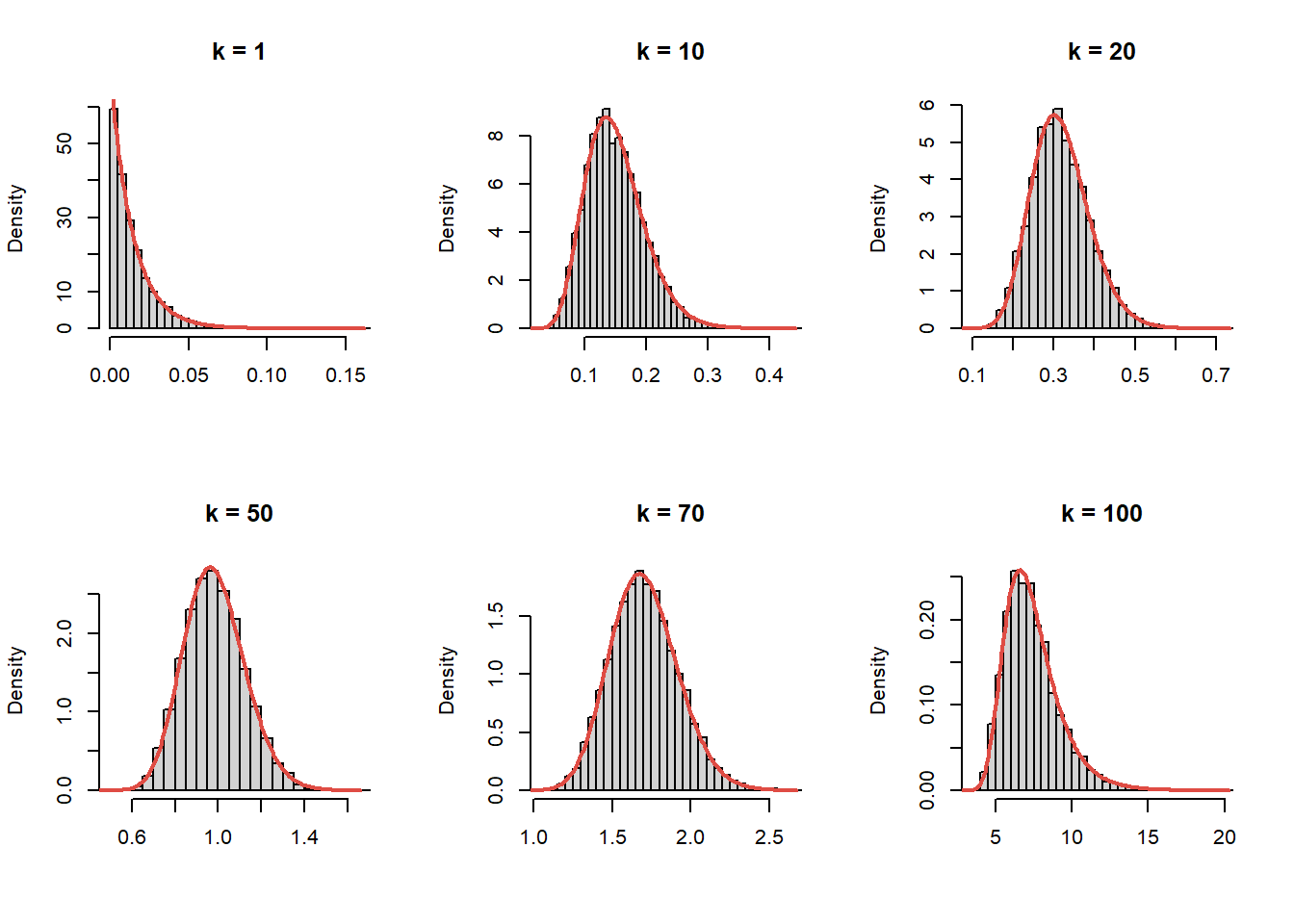
Figura 5.2: Ilustrarea densităților de repartiție ale statisticilor de ordin \(k\), pentru \(k\in\{1, 10, 20, 50, 70, 100\}\) în cazul \(\mathrm{Exp}(0.7)\)

3. Pentru compararea repartițiilor empirice cu cele teoretice avem

# simulare
N <- 10000
n <- 100

lambda <- 0.7
k <- c(1, 10, 20, 50, 70, n)

X_k <- matrix(0, nrow = N, ncol = length(k))

for (i in 1:N){
  x <- rexp(n, lambda)
  x_s <- sort(x)
  
  X_k[i, ] <- x_s[k]
}

par(mfrow = c(2, 3))

for (i in 1:length(k)){
     hist(X_k[, i], 
          probability = TRUE, 
          breaks = 30, xlab = "",
          main = paste0("k = ", k[i]))
     
     t <- seq(0, max(X_k[, i]), length.out = 200)
     lines(t, 
           dens_stat_ord_k(t, n, k[i], lambda),  
           lwd = 2, 
           col = myred)
}

Figura 5.3: Compararea repartițiilor empirice cu cele teoretice pentru statisticile de ordin \(k\), \(k\in\{1, 10, 20, 50, 70, 100\}\), în cazul \(\mathrm{Exp}(0.7)\)

Următorul rezultat ne arată care este repartiția comună a statisticilor de ordine:

Propoziția 5.2 (Densitatea comună a statisticilor de ordine) Fie \(X_1, X_2,\ldots, X_n\) variabile aleatoare i.i.d. cu densitatea de repartiție \(f\) unde \(f(x)>0\) pentru \((-\infty \leq) a<x<b(\leq \infty)\), altfel este egală cu \(0\), și fie \(X_{(1)}, X_{(2)},\ldots,X_{(n)}\) statisticile de ordine corespunzătoare. Dacă notăm cu \(g\) densitatea de repartiție comună a vectorului \(\left(X_{(1)}, X_{(2)},\ldots,X_{(n)}\right)\) atunci

\[ g\left(y_1, \ldots, y_n\right)= \begin{cases}n ! f\left(y_1\right) \cdots f\left(y_n\right), & a<y_1<y_2<\cdots<y_n<b \\ 0, & \text { altfel }\end{cases} \]

Demonstrație. Vom demonstra rezultatul pentru cazul \(n = 3\), cazul general putând fi tratat în mod similar. Să observăm pentru început că dacă \(i\neq j\) avem, din independență,

\[ \mathbb{P}\left(X_i=X_j\right)=\iint_{\left\{x_i=x_j\right\}} f\left(x_i\right) f\left(x_j\right) d x_i d x_j=\int_a^b \int_{x_j}^{x_j} f\left(x_i\right) f\left(x_j\right) d x_i d x_j=0, \]

ceea ce implică faptul că \(\mathbb{P}\left(X_i=X_j=X_k\right)=0\) pentru \(i\neq j\neq k\).

Cum densitatea de repartiție comună a vectorului \((X_1, X_2, X_3)\) este

\[ f\left(x_1, x_2, x_3\right)= \begin{cases}f\left(x_1\right) f\left(x_2\right) f\left(x_3\right), & a<x_1 \neq x_2 \neq x_3<b \\ 0, & \text { altfel, }\end{cases} \]

concluzionăm că \(f\) este nenulă și pozitivă (din ipoteză) pe mulțimea

\[ A = \left\{\left(x_1, x_2, x_3\right)^{\intercal} \in \mathbb{R}^3 ;\, a<x_i<b,\, i=1,2,3,\, x_1 \neq x_2 \neq x_3\right\} . \]

Fie partiția \(A_{i j k} \subset A\) cu \(A=\bigcup_{i, j, k} A_{i j k}\) unde

\[ A_{i j k}=\left\{\left(x_1, x_2, x_3\right)^{\intercal} ; a<x_i<x_j<x_k<b\right\}, \quad i, j, k=1,2,3, \quad i \neq j \neq k \]

Pentru fiecare \(A_{i j k}\) există o transformare bijectivă \(h_{ijk}:A_{ijk}\mapsto A_{123}\) (\((x_1,x_2,x_3)\mapsto (y_1, y_2, y_3)\) cu \(y_1<y_2<y_3\)) definită după cum urmează

\[ \begin{array}{llll} A_{123}: & y_1=x_1, & y_2=x_2, & y_3=x_3 \\ A_{132}: & y_1=x_1, & y_2=x_3, & y_3=x_2 \\ A_{213}: & y_1=x_2, & y_2=x_1, & y_3=x_3 \\ A_{231}: & y_1=x_2, & y_2=x_3, & y_3=x_1 \\ A_{312}: & y_1=x_3, & y_2=x_1, & y_3=x_2 \\ A_{321}: & y_1=x_3, & y_2=x_2, & y_3=x_1 . \end{array} \]

Inversele acestor aplicații, \(h_{ijk}^{-1}\), sunt date de

\[ \begin{array}{llll} A_{123}: & x_1=y_1, & x_2=y_2, & x_3=y_3 \\ A_{132}: & x_1=y_1, & x_2=y_3, & x_3=y_2 \\ A_{213}: & x_1=y_2, & x_2=y_1, & x_3=y_3 \\ A_{231}: & x_1=y_3, & x_2=y_1, & x_3=y_2 \\ A_{312}: & x_1=y_2, & x_2=y_3, & x_3=y_1 \\ A_{321}: & x_1=y_3, & x_2=y_2, & x_3=y_1 . \end{array} \]

Determinanții matricilor Jacobiene corespunzătoare acestor transformări sunt date de

\[ \begin{aligned} A_{123}:& \quad J_{123}=\left|\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right|=1 ; \quad & A_{231}: \quad J_{231}=\left|\begin{array}{lll} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right|=1 \\ A_{132}:& \quad J_{132}=\left|\begin{array}{lll} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right|=-1 ; \quad & A_{312}: \quad J_{312}=\left|\begin{array}{lll} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{array}\right|=1 \\ A_{213}:& \quad J_{213}=\left|\begin{array}{lll} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right|=-1 ; \quad & A_{321}: \quad J_{321}=\left|\begin{array}{lll} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{array}\right|=-1 \end{aligned} \]

Observăm că \(\left|J_{123}\right|=\cdots=\left|J_{321}\right|=1\), de unde găsim că

\[ \begin{aligned} g\left(y_1, y_2, y_3\right)&=\sum_{i, j, k} f\left(h_{i j k}^{-1}\left(y_1, y_2, y_3\right)\right)\left|J_{i j k}\right| \mathbb{1}_{A_{123}}{\left(y_1, y_2, y_3\right)}\\ &= f\left(y_1\right) f\left(y_2\right) f\left(y_3\right)+f\left(y_1\right) f\left(y_3\right) f\left(y_2\right)+f\left(y_2\right) f\left(y_1\right) f\left(y_3\right) \\ &\quad +f\left(y_3\right) f\left(y_1\right) f\left(y_2\right)+f\left(y_2\right) f\left(y_3\right) f\left(y_1\right)+f\left(y_3\right) f\left(y_2\right) f\left(y_1\right) \\ \end{aligned} \]

astfel

\[ g\left(y_1, y_2, y_3\right) = \begin{cases}3! f\left(y_1\right) f\left(y_2\right) f\left(y_3\right), & a<y_1<y_2<y_3<b \\ 0, & \text { alffel. }\end{cases} \]

Ca aplicație imediată a Propoziția 5.2 să observăm că dacă \(X_1, X_2,\ldots, X_n\sim\mathcal{U}(\alpha, \beta)\) atunci densitatea comună a a vectorului \(\left(X_{(1)}, X_{(2)},\ldots,X_{(n)}\right)\) este

\[ g\left(y_1, \ldots, y_n\right)= \begin{cases}\frac{n !}{(\beta-\alpha)^n}, & \alpha<y_1<y_2<\cdots<y_n<\beta \\ 0, & \text { altfel. }\end{cases} \]

Remarcă

Expresia densității comune a perechii \(\left(X_{(i)}, X_{(j)}\right)\) se poate determina euristic folosind argumentul bazat pe repartiția multinomială. În acest caz, considerăm categoriile următoare

\[ \begin{array}{cccc} \hline \text { Categoria} & \text { Descriere } & \text { Probabilitatea } & \text { \# Observații} \\ \hline 1 & \text{Mai mic decât } x & p_1 = F\left(x\right) & i-1 \\ 2 & \text{Aproximativ egal cu } x & p_2 = \text{" } f\left(x\right) \text{ "} & 1 \\ 3 & \text{Între } x \text{ și } y & p_3 = F\left(y\right)-F\left(x\right) & j-1-i \\ 4 & \text{Aproximativ egal cu } y & p_4 = \text{" } f\left(y\right) \text{ "} & 1 \\ 5 & \text{Mai mare decât } y & p_5 = 1-F\left(y\right) & n-j \\ \hline \end{array} \]

și găsim că

\[ \begin{aligned} f_{\left(X_{(i)}, X_{(j)}\right)}\left(x, y\right)&= \binom{n}{i-1, 1, j-1-i, 1, n-j}p_1^{i-1}p_2^{1}p_3^{j-1-i}p_4^{1}p_5^{n-j}\\ &= \frac{n !}{(i-1) !(j-1-i) !(n-j) !}\left[F\left(x\right)\right]^{i-1} f\left(x\right)\left[F\left(y\right)-F\left(x\right)\right]^{j-1-i} f\left(y\right)\left[1-F\left(y\right)\right]^{n-j} \end{aligned} \]

Următoarele exerciții fac referire la modul în care este repartizată amplitudinea (range) eșantionului. Știm că dacă \(X_1,X_2,\ldots,X_n\) este un eșantion de volum \(n\) dintr-o populație dată atunci statistica \(R_n = X_{(n)} - X_{(1)}\) se numește amplitudinea eșantionului (în engleză range) și este o statistică care oferă o imagine a gradului de împrăștiere a datelor.

Exercițiul 5.2 (Densitatea amplitudinii eșantionului) Fie \(X_1,X_2,\ldots,X_n\sim F\), un eșantion de volum \(n\) din populația \(F\).

1. Să se determine funcția de repartiție a vectorului \(\left(X_{(1)}, X_{(n)}\right)\)
2. Dacă \(F\) admite densitatea de repartiție \(f\) atunci să se determine densitatea amplitudinii eșantionului \(R_n = X_{(n)} - X_{(1)}\).

Soluție. Pentru primul punct avem:

1. Funcția de repartiție a vectorului \(\left(X_{(1)}, X_{(n)}\right)\) este

\[ \begin{aligned} F_{\left(X_{(1)}, X_{(n)}\right)}(x, y) &= \mathbb{P}\left(X_{(1)}\leq x, X_{(n)}\leq y\right) = \mathbb{P}\left(X_{(n)}\leq y\right) - \mathbb{P}\left(X_{(1)}> x, X_{(n)}\leq y\right) \\ &= \mathbb{P}\left(X_1\leq y, \ldots, X_n\leq y\right) - \mathbb{P}\left(X_{(1)}> x, X_{(n)}\leq y\right) \\ &\stackrel{indep}{=} \prod_{i=1}^{n}\mathbb{P}\left(X_i\leq y\right) - \mathbb{P}\left(X_{(1)}> x, X_{(n)}\leq y\right)\\ &= F(y)^n - \mathbb{P}\left(X_{(1)}> x, X_{(n)}\leq y\right) \end{aligned} \]

Dacă \(y \leq x\) atunci \(\{X_{(n)}\leq y \leq x < X_{(1)}\} = \emptyset\) deci \(\mathbb{P}\left(X_{(1)}> x, X_{(n)}\leq y\right) = 0\) iar dacă \(y > x\) atunci

\[ \{X_{(1)}> x, X_{(n)}\leq y\} = \{x < X_{(1)}\leq X_{(n)}\leq y\} = \bigcap_{i=1}^{n}\{x < X_i\leq y\} \]

de unde

\[ \begin{aligned} \mathbb{P}\left(X_{(1)}> x, X_{(n)}\leq y\right) &= \mathbb{P}\left(\bigcap_{i=1}^{n}\{x < X_i\leq y\}\right) = \prod_{i=1}^{n}\mathbb{P}\left(x < X_i\leq y\right) \\ &= \prod_{i=1}^{n}\left[\mathbb{P}\left(X_i\leq y\right) - \mathbb{P}\left(X_i\leq x\right)\right] = \prod_{i=1}^{n}\left[F(y) - F(x)\right]\\ &= \left[F(y) - F(x)\right]^n \end{aligned} \]

Astfel rezultă că

\[ F_{\left(X_{(1)}, X_{(n)}\right)}(x, y) = \left\{\begin{array}{ll} F(y)^n, & \text{dacă } y\leq x\\ F(y)^n - \left[F(y) - F(x)\right]^n, & \text{dacă } y > x \end{array}\right. \]

2. Dacă \(X_i\) admite densitatea de repartiție \(f\) atunci densitatea de repartiție a vectorului \(\left(X_{(1)}, X_{(n)}\right)\) este

\[ \begin{aligned} f_{\left(X_{(1)}, X_{(n)}\right)}(x, y) &= \frac{\partial^2 F_{\left(X_{(1)}, X_{(n)}\right)}(x, y)}{\partial x \partial y}\\ &= \left\{\begin{array}{ll} 0, & \text{dacă } y\leq x\\ n(n-1)\left[F(y) - F(x)\right]^{n-2}f(x)f(y), & \text{dacă } y > x \end{array}\right. \end{aligned} \]

Pentru a determina densitatea de repartiția a statisticii \(R_n = X_{(n)} - X_{(1)}\), vom calcula densitatea comună a vectorului \((R_n,X_{(1)}) = \left(X_{(n)} - X_{(1)}, X_{(1)}\right)\) și, plecând de la aceasta, vom găsi repartiția marginală a lui \(R_n\). Considerăm transformarea \(g: A\to B\) definită prin

\[ g:(x, y) \mapsto(u, v)=\left(y-x, x\right) \]

astfel că \((R_n,X_{(1)}) = g(X_{(1)}, X_{(n)})\). Funcția \(g\) este bijectivă iar inversa ei este dată de

\[ g^{-1}:(u, v) \mapsto\left(v, u + v\right). \]

Matricea Jacobiană corespunzătoare lui \(g^{-1}\) este

\[ J_{g^{-1}}=\left(\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\right) \]

de unde găsim determinantul \(\operatorname{det}\left(J_{g^{-1}}(u, v)\right)=-1\). Ținând cont de faptul că densitatea comună a vectorului \(\left(X_{(1)}, X_{(n)}\right)\) este

\[ f_{\left(X_{(1)}, X_{(n)}\right)}(x, y) = \left\{\begin{array}{ll} 0, & \text{dacă } y\leq x\\ n(n-1)\left[F(y) - F(x)\right]^{n-2}f(x)f(y), & \text{dacă } y > x \end{array}\right. \]

atunci densitatea comună a vectorului \(\left(R_n,X_{(1)}\right)\) este, pentru \(u\geq 0\),

\[ \begin{aligned} f_{\left(R_n,X_{(1)}\right)}(u, v) & =f_{\left(X_{(1)}, X_{(n)}\right)}\left(g^{-1}(u, v)\right)\left|\operatorname{det}\left(J_{g-1}(u, v)\right)\right|=f_{\left(X_{(1)}, X_{(n)}\right)}\left(v , u+v\right) |1|\\ & = n(n-1)\left[F(u + v) - F(v)\right]^{n-2}f(u)f(u+v). \end{aligned} \]

Integrând în raport cu \(v\) avem că densitatea marginală a lui \(R_n\) este

\[ \begin{aligned} f_{R_n}(u) & = \left\{\begin{array}{ll} n(n-1)\int\left[F(u + v) - F(v)\right]^{n-2}f(u)f(u+v) \,dv, & \text{dacă } u > 0\\ 0, & \text{dacă } u\leq 0\\ \end{array}\right. \end{aligned} \]

Exercițiul 5.3 (Amplitudinea eșantionului în populații uniforme) Fie \(X_1,X_2,\ldots,X_n\sim F\), un eșantion de volum \(n\) din populația \(\mathcal{U}(0, 1)\).

1. Să se determine densitatea amplitudinii eșantionului \(R_n = X_{(n)} - X_{(1)}\)
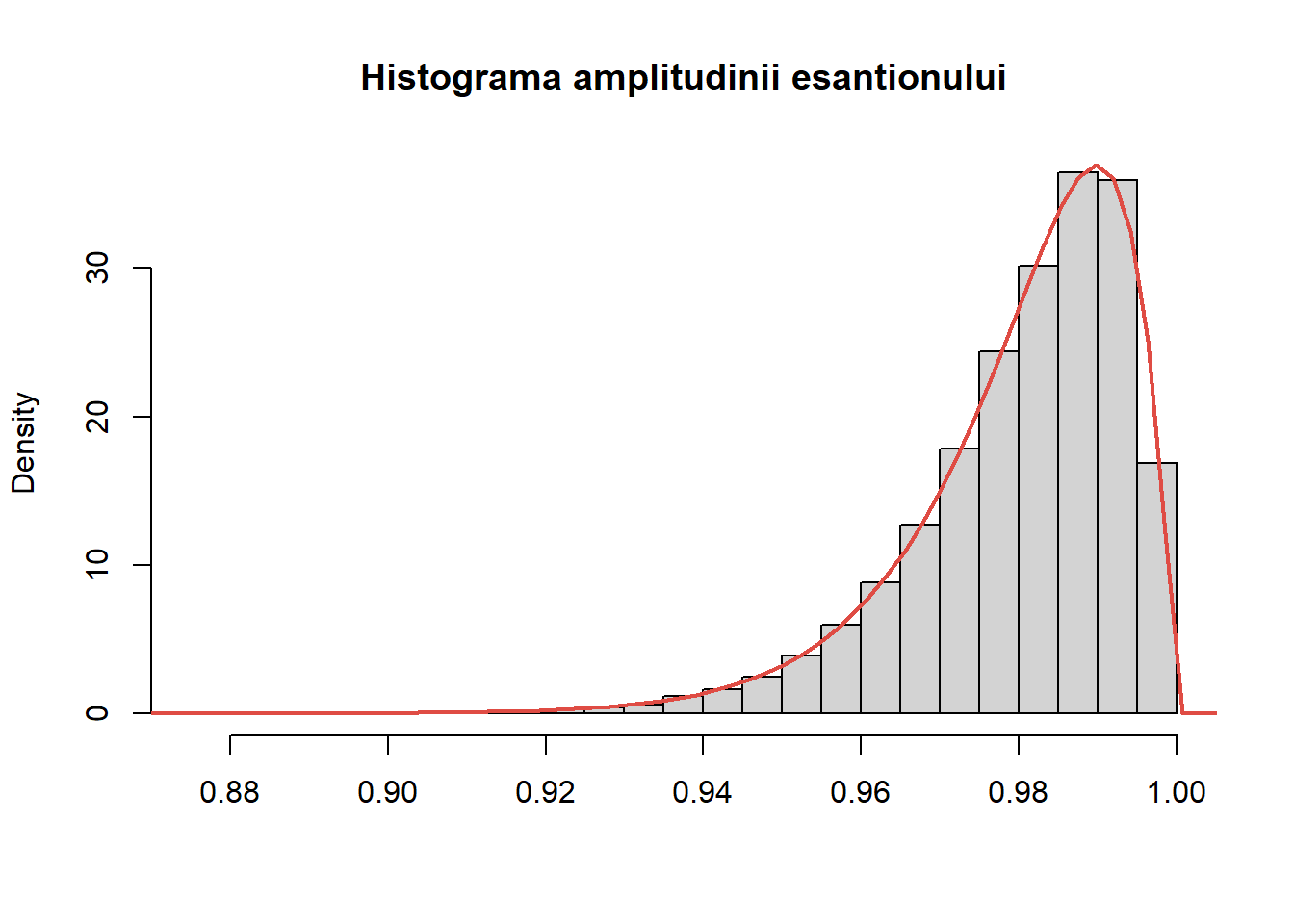
2. Generați \(N = 10000\) de eșantioane de volum \(n=100\) din \(\mathcal{U}(0, 1)\), calculați amplitudinea eșantionului și comparați grafic (prin intermediul unei histograme) repartiția empirică cu cea teoretică.
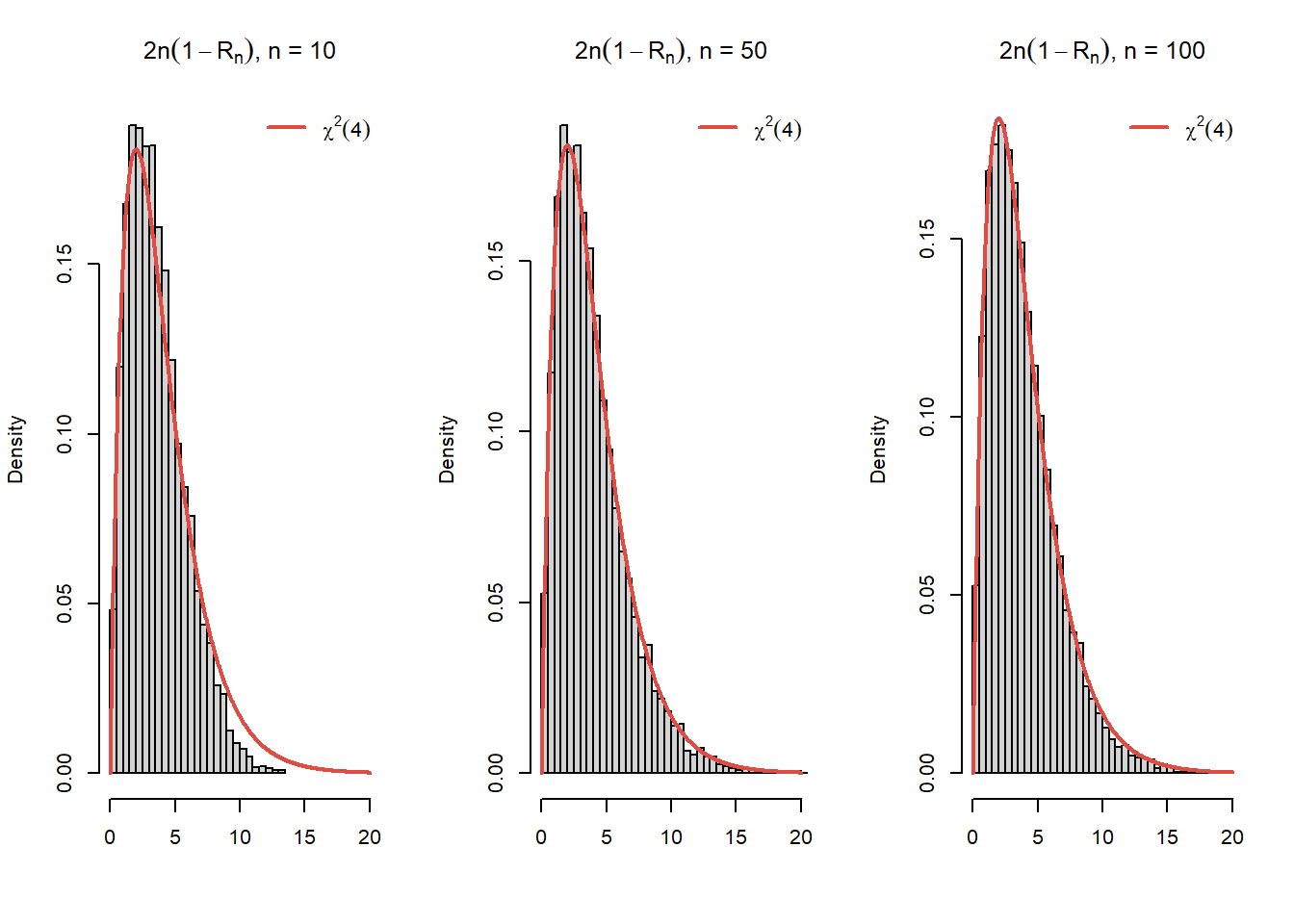
3. Arătați că repartiția limită a variabilei \(2n(1-R_n)\) este \(\chi^2(4)\).

Soluție. Avem pentru primul punct:

1. Din Exercițiul 5.2 am văzut că densitatea amplitudinii eșantionului este

\[ \begin{aligned} f_{R_n}(u) & = \left\{\begin{array}{ll} n(n-1)\int\left[F(u + v) - F(v)\right]^{n-2}f(u)f(u+v) \,dv, & \text{dacă } u > 0\\ 0, & \text{dacă } u\leq 0\\ \end{array}\right. \end{aligned} \]

și pentru cazul repartiției \(\mathcal{U}(0, 1)\) acest rezultat se reduce la

\[ f_{R_n}(u) = n(n-1) \int_0^{1-u} u^{n-2} d x = n (n-1) u^{n-2}(1-u), \quad 0<u<1 \]

Se observă, în plus, că densitatea amplitudinii pentru cazul \(\mathcal{U}(0, 1)\) se reduce la

\[ f_{R_n}(u) = \frac{\Gamma(n+1)}{\Gamma(n-1) \Gamma(2)} u^{(n-1)-1}\left(1-u\right)^{2-1} \]

ceea ce arată că \(R_n\) este repartizată Beta \(B(n-1, 2)\).

2. Pentru al doilea punct, avem următoarea funcție care implementează densitatea \(f_{R_n}\)

range_unif <- function(u, n=1){
     # uniforma pe (0, 1)
     # n - volumul esantionului
     
     return(ifelse((0<=u) & (u<=1), n*(n-1)*u^(n-2)*(1-u), 0))
}

și următorul cod care permite compararea repartiției empirice cu cea teoretică

# simulare
N <- 10000
n <- 100

Rn <- numeric(N)

for (i in 1:N){
  x <- runif(n)
  Rn[i] <- max(x) - min(x)
}

hist(Rn, 
     probability = TRUE,
     breaks = 30, xlab = "",
     main = "Histograma amplitudinii esantionului")
     
t <- seq(0, 1.1, length.out = 500)
lines(t, 
      range_unif(t, n = n),  
      lwd = 2, 
      col = myred)

Figura 5.4: Compararea repartiției empirice a amplitudinii eșantionului cu cea teoretică

3. Dacă notăm cu \(Y = 2n\left(1-R_n\right)\) atunci

\[ \begin{aligned} F_{Y}(x) &= \mathbb{P}\left(Y\leq x\right) = \mathbb{P}\left(2n\left(1-R_n\right)\leq x\right)\\ &= \mathbb{P}\left(R_n\geq 1-\frac{x}{2n}\right) = 1 - \mathbb{P}\left(R_n< 1-\frac{x}{2n}\right)\\ &= 1 - F_{R_n}\left(1-\frac{x}{2n}\right) \end{aligned} \]

ceea ce conduce la

\[ \begin{aligned} f_{Y}(x) &= \frac{d F_{Y}(x)}{dx} = \frac{1}{2n}f_{R_n}\left(1-\frac{x}{2n}\right)\\ &= \frac{1}{2n}n (n-1) \left(1-\frac{x}{2n}\right)^{n-2}\left[1-\left(1-\frac{x}{2n}\right)\right]\mathbf{1}_{(0,1)}\left(1-\frac{x}{2 n}\right)\\ &= \begin{cases}\frac{n-1}{4 n} x\left(1-\frac{x}{2 n}\right)^{n-2} & 0<x<2 n \\ 0 & \text { altfel }\end{cases} \end{aligned} \]

Cum \(\lim_{n\to\infty}\left(1-\frac{x}{2 n}\right)^{n-2} = e^{-\frac{x}{2}}\) și \(\frac{n-1}{4 n}\to\frac{1}{4}\) găsim că

\[ \lim_{n\to\infty}f_{Y}(x) = \frac{1}{4}x e^{-\frac{x}{2}}\mathbf{1}_{(0,\infty)}(x). \]

Aplicând Lema lui Scheffe deducem că repartiția limită a variabilei \(2n(1-R_n)\) este \(\chi^2(4)\).

Figura de mai jos ilustrează acest proces:

N <- 10000
n <- c(10, 50, 100)

Y <- matrix(0, nrow = N, ncol = length(n))

for (i in 1:N){
     x1 <- runif(n[1])
     Y[i, 1] <- 2*n[1]*(1 - max(x1) + min(x1))
     
     x2 <- runif(n[2])
     Y[i, 2] <- 2*n[2]*(1 - max(x2) + min(x2))
     
     x3 <- runif(n[3])
     Y[i, 3] <- 2*n[3]*(1 - max(x3) + min(x3))
}

f_lim <- function(x){dchisq(x, df = 4)}

par(mfrow = c(1, length(n)))

for (j in 1:length(n)){
     
hist(Y[, j], 
     probability = TRUE,
     xlim = c(0, 20),
     breaks = 30, xlab = "",
     main = TeX(paste0("$2n(1- R_n)$,", " n = ", n[j])))
     
t <- seq(0, 20, length.out = 500)
lines(t, 
      f_lim(t),  
      lwd = 2, 
      col = myred)

legend("topright", 
       legend = TeX("$\\chi^2(4)$"), 
       col = myred, 
       lwd = 2, bty = "n")
}

Figura 5.5: Ilustrarea repartiției asimptotice a v.a. \(2n(1 - R_n)\)

Funcția de repartiție empirică

Fie \(X_1,X_2,\ldots,X_n\) un eșantion de volum \(n\) dintr-o populație a cărei funcție de repartiție este \(F\). Funcția de repartiție empirică este definită, pentru toate valorile \(x\in\mathbb{R}\), prin

\[ \hat{F}_n(x) = \frac{1}{n}\sum_{i = 1}^{n}\mathbb{1}_{(-\infty, x]}(X_i) = \frac{1}{n}\sum_{i = 1}^{n}\mathbb{1}_{(-\infty, x]}(X_{(i)}) \]

unde \(X_{(1)}, X_{(2)}, \ldots, X_{(n)}\) reprezintă statisticile de ordine. Observăm că, notând \(X_{(n+1)} = +\infty\), avem

\[ \hat{F}_n(x) = \sum_{i = 1}^{n}\frac{i}{n}\mathbf{1}_{\left[X_{(i)}, X_{(i+1)}\right)}(x). \]

Funcția de repartiție empirică verifică:

Propoziția 6.1 Dacă \(\hat{F}_n(x)\) este funcția de repartiție empirică asociată unui eșantion de talie \(n\), dintr-o populație a cărei funcție de repartiție este \(F\), atunci, pentru \(x\in\mathbb{R}\):

1. variabila aleatoare \(n\hat{F}_n(x)\) este repartizată binomial \(\mathcal{B}(n, F(x))\)
2. are loc convergența (LNM): \(\hat{F}_n(x)\overset{a.s.}{\to} F(x)\)
3. are loc proprietatea de normalitate asimptotică (TLC): \(\sqrt{n}(\hat{F}_n(x) - F(x))\overset{d}{\to}\mathcal{N}(0,F(x)(1-F(x)))\).

Demonstrație. Fie \(x\in\mathbb{R}\) fixat și definim variabilele aleatoare \(Y_i = \mathbf{1}_{(-\infty, x]}(X_i)\), \(1\leq i\leq n\). Cum \(X_1,X_2,\ldots,X_n\) sunt i.i.d. deducem că \(Y_1,Y_2,\ldots,Y_n\) sunt i.i.d. și în plus \(Y_i\sim \mathcal{B}(p)\) cu \(p = \mathbb{P}(Y_1 = 1) = F(x)\).

Din definiția funcției de repartiție empirică avem

\[ \hat{F}_n(x) = \frac{1}{n}\sum_{i = 1}^{n}\mathbf{1}_{(-\infty, x]}(X_i) = \frac{1}{n}\sum_{i = 1}^{n}Y_i \]

și aplicând Legea Tare a Numerelor Mari obținem

\[ \hat{F}_n(x) = \frac{1}{n}\sum_{i = 1}^{n}Y_i \overset{a.s.}{\underset{n\to\infty}\longrightarrow} \mathbb{E}[Y_1] = F(x). \]

În mod similar aplicând Teorema Limită Centrală deducem

\[ \sqrt{n}(\hat{F}_n(x) - F(x))\overset{d}{\underset{n\to\infty}\longrightarrow}\mathcal{N}(0,Var(Y_1)) = \mathcal{N}(0,F(x)(1-F(x))). \]

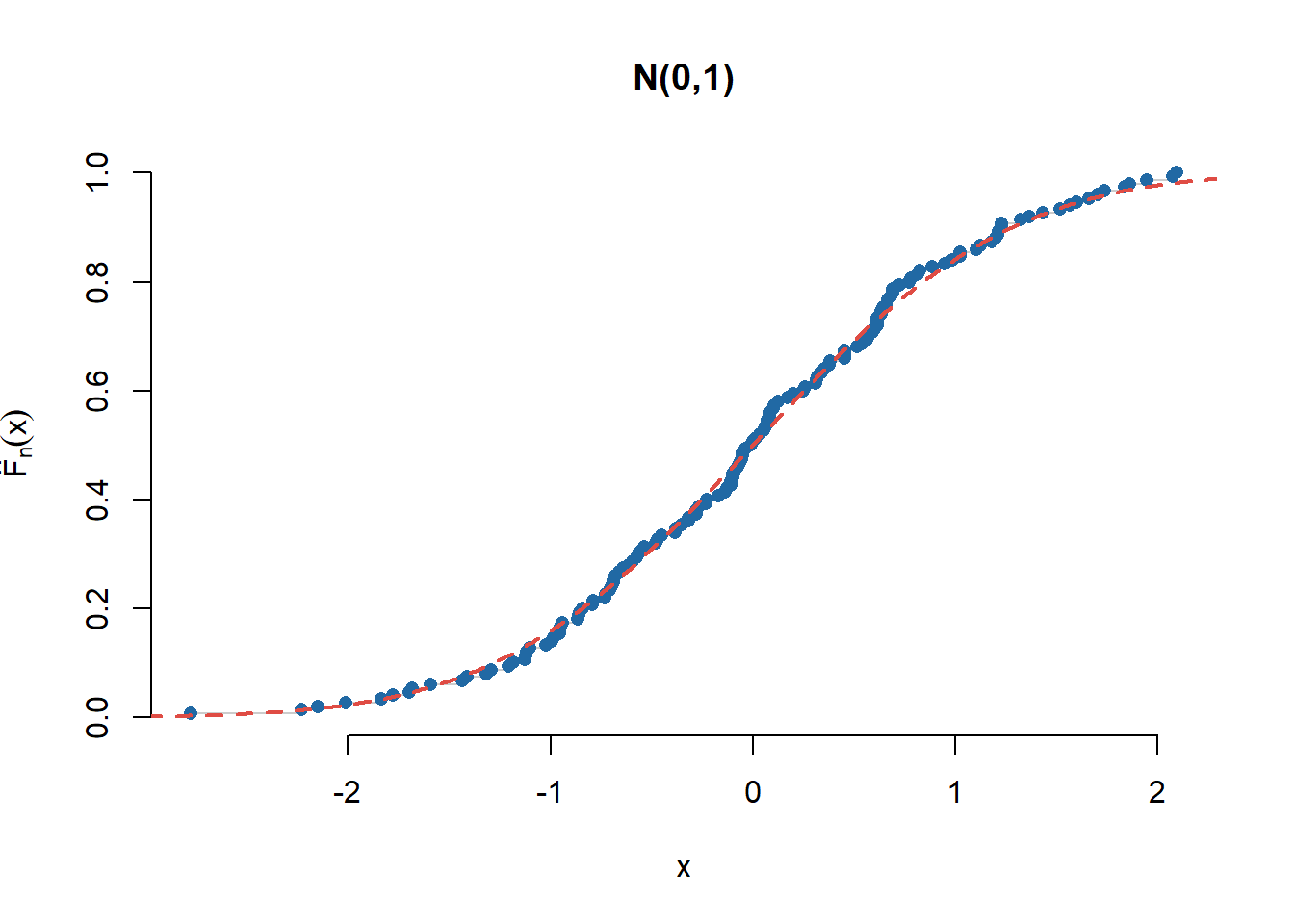
Exercițiul 6.1 Ilustrați grafic rezultatele din Propoziția 6.1 pentru o populație repartizată \(\mathcal{N}(0,1)\) și respectiv \(\mathrm{Exp}(3)\). Pentru proprietatea de normalitate considerați \(x_0 = 2\) și respectiv \(x_0 = 1.5\).

Soluție. Pentru ilustrarea repartiției empirice, în cazul \(\mathcal{N}(0,1)\), avem următorul cod

n <- 150 
x <- rnorm(n)

plot(sort(x), (1:n)/n, type = "s", 
     main = "N(0,1)", bty = "n", 
     col = "grey80",
     xlab = "x", 
     ylab = expression(hat(F)[n](x)))
points(sort(x), (1:n)/n, pch = 16,
       col = myblue)
lines(seq(-3,3,0.01), pnorm(seq(-3,3,0.01)),
      col = myred, lwd = 2, lty = 2)

Figura 6.1: Ilustrarea repartiției empirice pentru un eșantion \(\mathcal{N}(0,1)\).

Următoarea funcție generică ne permite să trasăm grafic funcția de repartiție empirică plecând de la un eșantion dat:

plot_ecdf <- function(x, ...){
  # trasarea functiei de repartitie empirice pentru esantionul x
  n <- length(x)
  xs <- sort(x)
  
  lx <- xs[1] - (xs[n] - xs[1])/10
  ux <- xs[n] + (xs[n] + xs[1])/10
  
  plot(c(lx, xs, ux), c(0, (1:n)/n, 1), 
       type = "s", 
       main = "Functia de repartitie empirica", 
       bty = "n", 
       xlab = "x", 
       ylab = expression(hat(F)[n](x)), 
       ...)
  
  points(xs, (1:n)/n,
         pch = 16, 
         cex = 0.5)
  
  abline(h = 0, 
         lty = 2)
  abline(h = 1, 
         lty = 2)
}

Pentru ilustrarea convergenței vom construi o funcție care ne permite să evaluăm funcția de repartiție empirică într-un punct

compute_ecdf <- function(x, esantion){
  n <- length(esantion)
  xs <- sort(esantion)
  
  out <- sum(xs <= x)/n
  
  return(out)
}

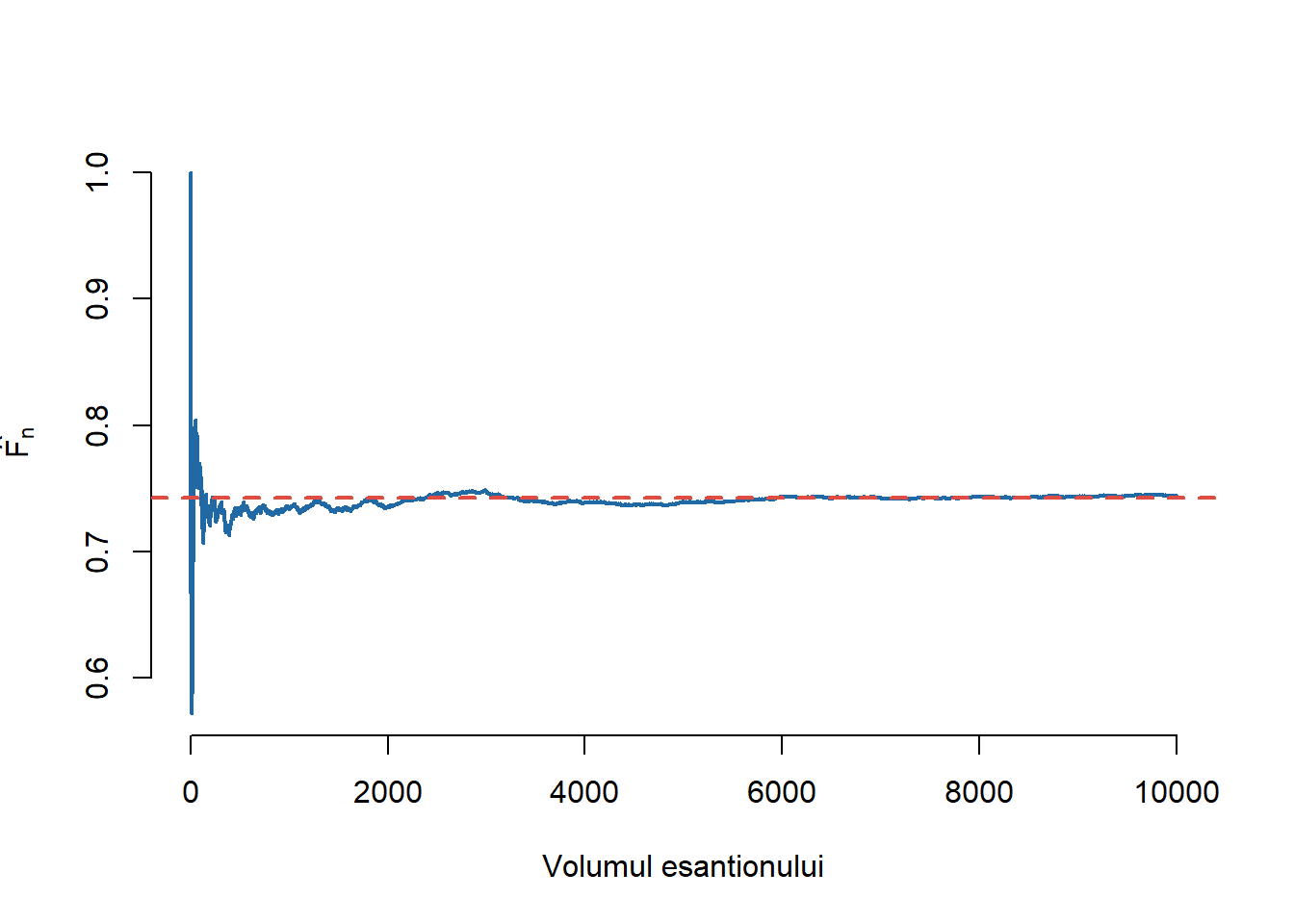
compute_ecdf <- Vectorize(compute_ecdf, vectorize.args = "x")

Convergența (LNM) este ilustrată în cele ce urmează:

# Simulare
x0 <- 0.65

N <- 10000

# Esantion
x <- rnorm(N)

Fn <- numeric(N)

for (i in 1:N){
  Fn[i] <- compute_ecdf(x0, x[1:i])
}

plot(1:N, Fn, 
     type = "l", lwd = 2,
     xlab = "Volumul esantionului",
     ylab = expression(hat(F[n])),
     col = myblue, 
     bty = "n")

abline(h = pnorm(x0), 
       col = myred, 
       lty = 2, lwd = 2)

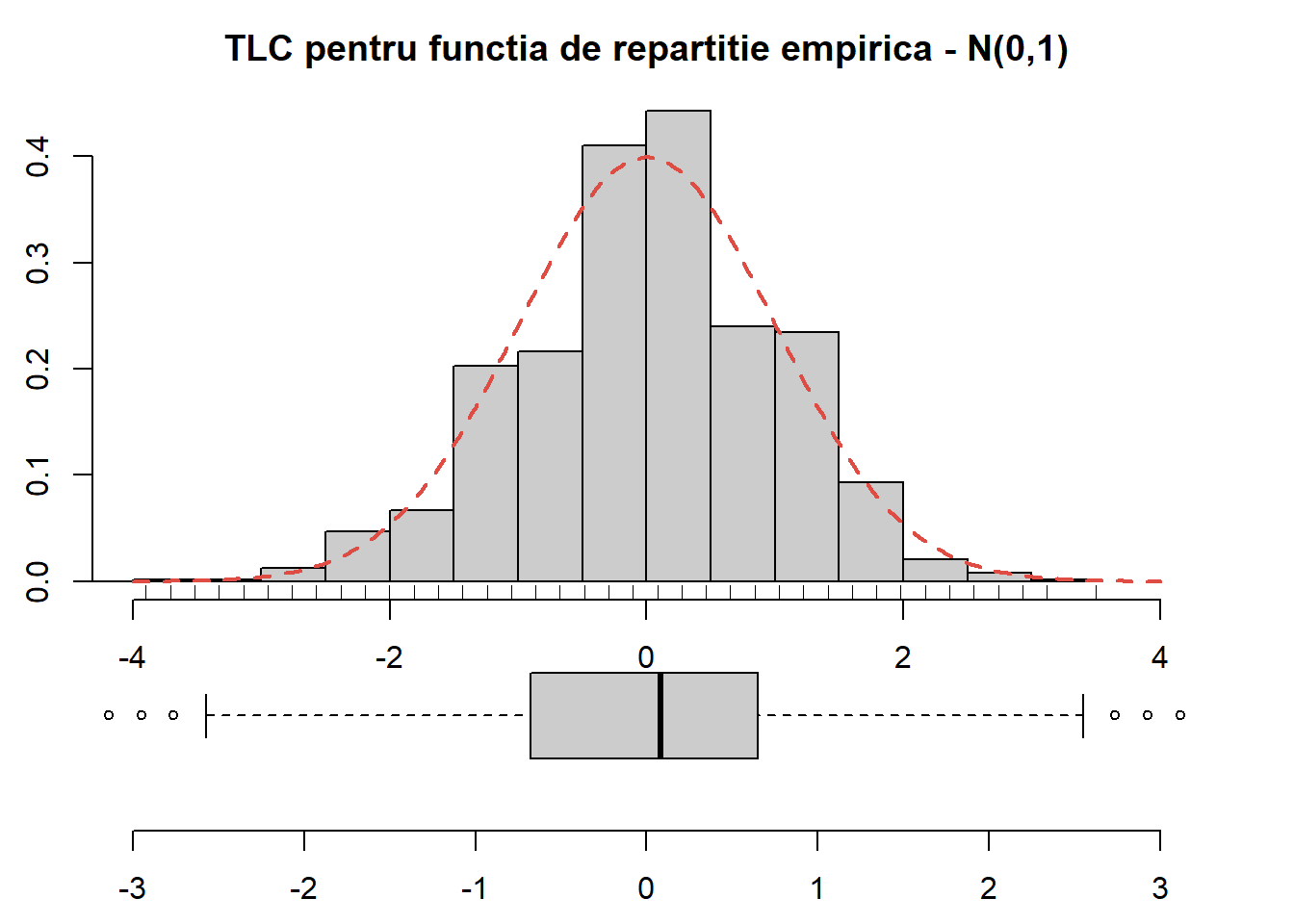
Figura 6.2: Ilustrarea convergenței repartiției empirice la repartiția teoretică în cazul \(\mathcal{N}(0,1)\).

Proprietatea de normalitate asimptotică (TLC) este ilustrată în Figura 6.3 de mai jos:

S <- 10000
n <- 1250

x0 <- 2
sigma_sq <- pnorm(x0)*(1-pnorm(x0))
sigma <- sqrt(sigma_sq)
Fx0 <- pnorm(x0)

Fn <- numeric(S) 

for (i in 1:S){
  x <- rnorm(n)
  Fn[i] <- (sum(x<=x0)/n - Fx0)*sqrt(n)/sigma
}

# plot
par(mai=c(0.5,0.5,0.5,0.5), bty = "n")

par(fig = c(0, 1, 0, 0.45))
boxplot(Fn, horizontal=T, bty="n", 
        xlab=expression(sqrt(n) (hat(F)[n] (2) - F(2))/sqrt(F(2)(1-F(2)))),
        col = "grey80",
        ylim = c(-3, 3), 
        cex = 0.7)

par(fig = c(0, 1, 0.25, 1), new = T)
hist(Fn, 
     probability = TRUE, 
     # breaks = seq(-4, 4, by = 0.5),
     xlim = c(-4, 4),
     col = "grey80",
     main = "TLC pentru functia de repartitie empirica - N(0,1)",
     xlab = "",
     ylab = "Densitatea")

lines(seq(-4, 4, length.out = 250),
      dnorm(seq(-4, 4, length.out = 250)), 
      type = "l", 
      col = myred, lty = 2, lwd = 2)
rug(Fn)

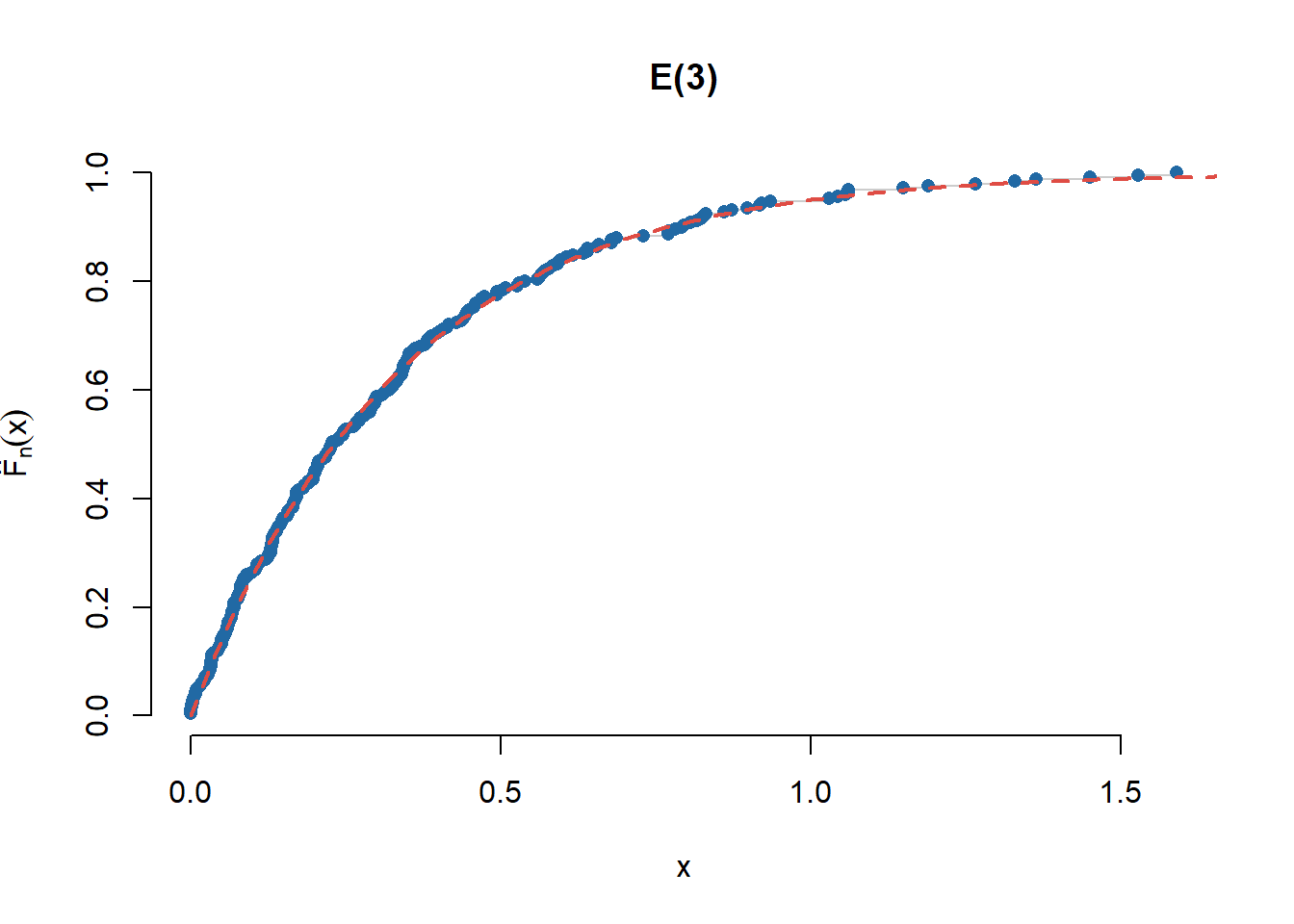
Figura 6.3: Ilustrarea proprietății de normalitate asimptotică în cazul \(\mathcal{N}(0,1)\).

Pentru repartiția \(\mathrm{Exp}(3)\) avem pentru început ilustrarea funcției de repartiție empirică

n <- 250 
x <- rexp(n, 3)

plot(sort(x), (1:n)/n, type = "s", 
     main = "E(3)", bty = "n", 
     col = "grey80",
     xlab = "x", 
     ylab = expression(hat(F)[n](x)))
points(sort(x), (1:n)/n, pch = 16,
       col = myblue)
lines(seq(0,3,0.01), pexp(seq(0,3,0.01), 3),
      col = myred, lwd = 2, lty = 2)

Figura 6.4: Ilustrarea funcției de repartiție empirice în cazul \(\mathrm{Exp}(3)\).

Proprietatea de convergență devine

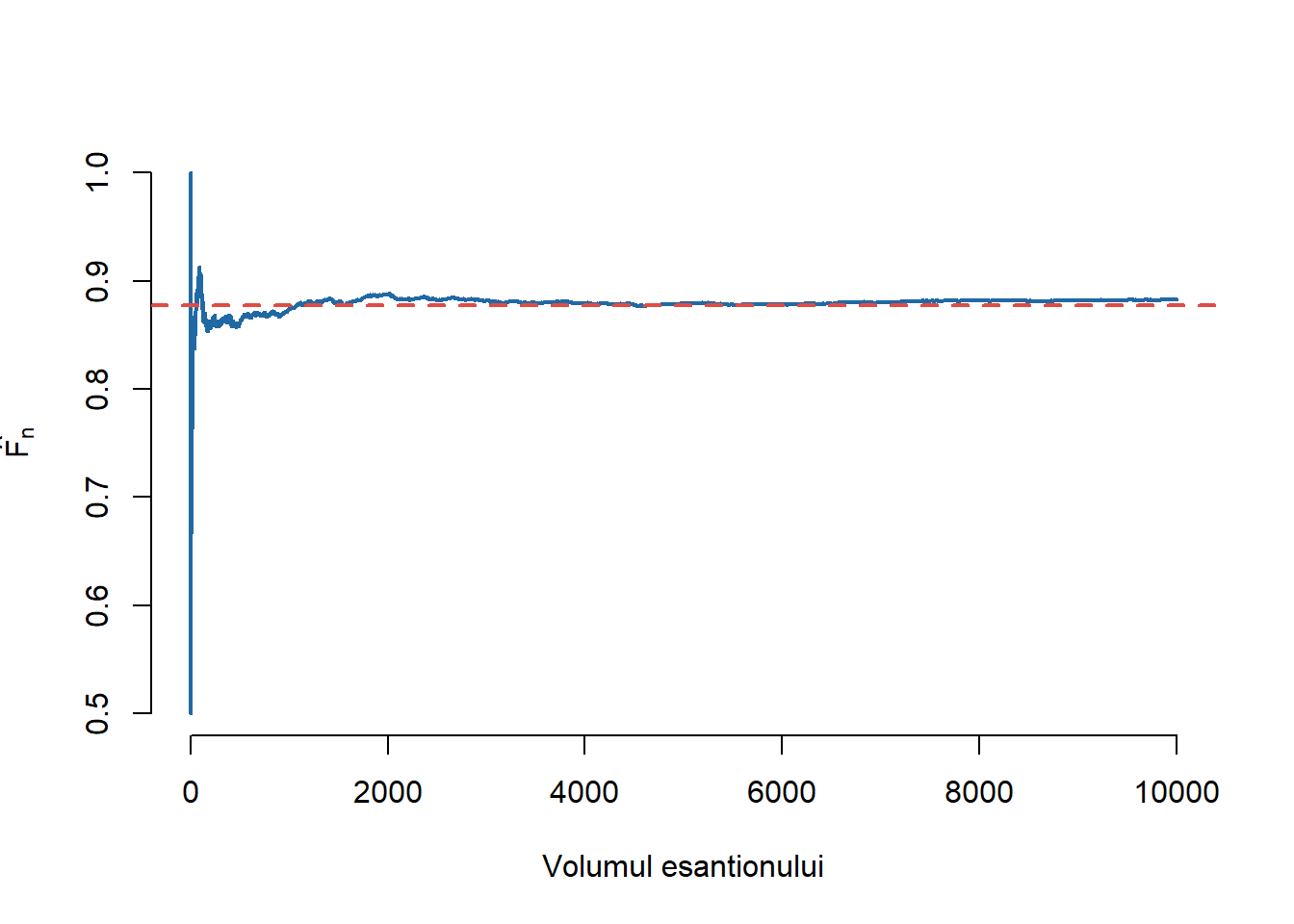
# Simulare
x0 <- 0.7

N <- 10000

# Esantion
x <- rexp(N, rate = 3)

Fn <- numeric(N)

for (i in 1:N){
  Fn[i] <- compute_ecdf(x0, x[1:i])
}

plot(1:N, Fn, 
     type = "l", lwd = 2,
     xlab = "Volumul esantionului",
     ylab = expression(hat(F[n])),
     col = myblue, 
     bty = "n")

abline(h = pexp(x0, rate = 3), 
       col = myred, 
       lty = 2, lwd = 2)

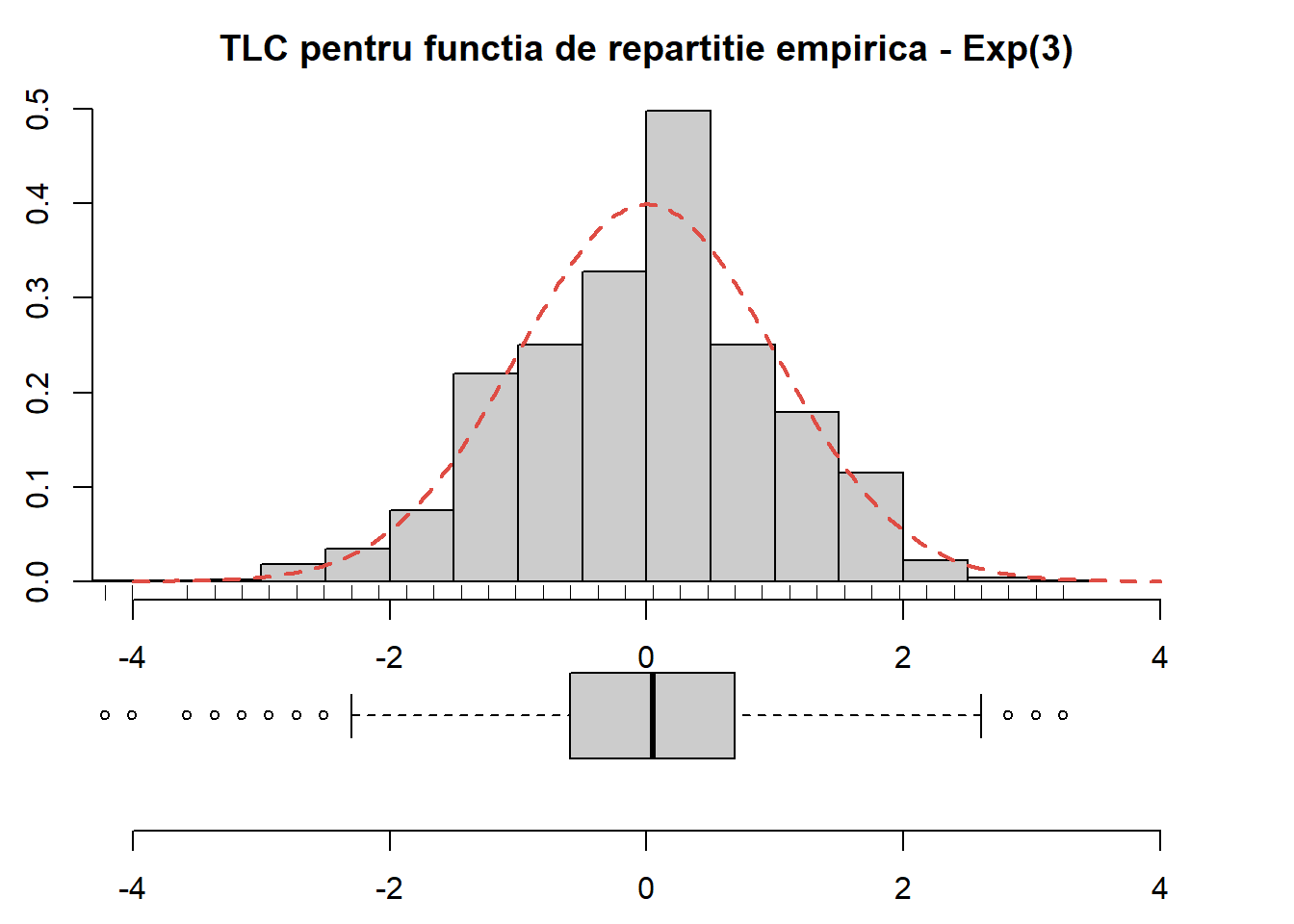
Figura 6.5: Ilustrarea convergenței repartiției empirice la repartiția teoretică în cazul \(\mathrm{Exp}(3)\).

Proprietatea de normalitate asimptotică este evidențiată în codul următor:

S <- 10000
n <- 2000

x0 <- 1.5
lambda <- 3

sigma_sq <- pexp(x0, lambda)*(1-pexp(x0, lambda))
sigma <- sqrt(sigma_sq)
Fx0 <- pexp(x0, lambda)

Fn <- numeric(S) 

for (i in 1:S){
  x <- rexp(n, lambda)
  Fn[i] <- (sum(x<=x0)/n - Fx0)*sqrt(n)/sigma
}

# plot
par(mai=c(0.5,0.5,0.5,0.5), bty = "n")

par(fig = c(0, 1, 0, 0.45))
boxplot(Fn, horizontal=T, bty="n", 
        xlab=expression(sqrt(n) (hat(F)[n] (1.5) - F(1.5))/sqrt(F(1.5)(1-F(1.5)))),
        col = "grey80",
        ylim = c(-4, 4), 
        cex = 0.7)

par(fig = c(0, 1, 0.25, 1), new = T)
hist(Fn, 
     probability = TRUE, 
     # breaks = seq(-4, 4, by = 0.5),
     xlim = c(-4, 4),
     col = "grey80",
     main = "TLC pentru functia de repartitie empirica - Exp(3)",
     xlab = "",
     ylab = "Densitatea")

lines(seq(-4, 4, length.out = 250),
      dnorm(seq(-4, 4, length.out = 250)), 
      type = "l", 
      col = myred, lty = 2, lwd = 2)
rug(Fn)

Figura 6.6: Ilustrarea proprietății de normalitate asimptotică în cazul \(\mathrm{Exp}(3)\).

Conform rezultatului anterior putem spune că \(\hat{F}_n(x)\) este un estimator rezonabil pentru funcția de repartiție \(F(x)\) dat fiind o valoare \(x\in\mathbb{R}\) fixată. Întrebarea care se pune este dacă \(\hat{F}_n(x)\) este un estimator rezonabil pentru întreaga funcție de repartiție \(F(x)\) ? Răspunsul la această întrebare este dat de Teorema Glivenko-Cantelli² de mai jos:

Teorema 6.1 (Teorema Glivenko-Cantelli) Fie \((X_n)_n\) un șir de variabile aleatoare independent și identic repartizate, cu funcția de repartiție comună \(F\). Atunci are loc

\[ \sup_{x\in\mathbb{R}}\left|\hat{F}_n(x) - F(x)\right| \overset{a.s.}{\underset{n\to\infty}\longrightarrow} 0. \]

Cuantile empirice

Reamintim că dată fiind o funcție de repartiție \(F\), funcția cuantilă (inversa generalizată) asociată lui \(F\), \(F^{-1}:(0,1)\to\mathbb{R}\) este definită prin

\[ F^{-1}(u) = \inf\{x\in\mathbb{R}\,|\,F(x)\geq u\}, \quad \forall u\in(0,1) \]

unde folosim convențiile \(\inf\mathbb{R} = -\infty\) și \(\inf\emptyset = +\infty\).

Propoziția 7.1 Funcția cuantilă \(F^{-1}\) verifică următoarele proprietăți:

1. Valoarea în \(0\): \(F^{-1}(0) = -\infty\)
2. Monotonie: \(F^{-1}\) este crescătoare
3. Continuitate: \(F^{-1}\) este continuă la stânga
4. Echivalență: pentru \(\forall u\in[0,1]\) avem \(F(x)\geq u \iff x\geq F^{-1}(u)\)
5. Inversabilitate: \(\forall u\in[0,1]\) avem \((F\circ F^{-1})(u)\geq u\). În plus
   1. dacă \(F\) este continuă atunci \(F\circ F^{-1} = Id\) dar dacă nu este injectivă atunci există \(x_0\) așa încât \((F^{-1}\circ F)(x_0)<x_0\)
   2. dacă \(F\) este injectivă atunci \(F^{-1}\circ F = Id\) dar dacă nu este continuă atunci există \(u_0\) astfel că \((F\circ F^{-1})(u_0)>u_0\)

Pentru a exemplifica punctul 5a, putem considera variabila aleatoare \(X\sim\mathcal{U}[0,1]\) a cărei funcție de repartiție \(F\) este continuă dar nu injectivă și în plus \((F^{-1}\circ F)(2) = F^{-1}(1) = 1 < 2\). Pentru punctul 5b să considerăm variabilele aleatoare \(Y\sim\mathcal{N}(0,1)\) și \(B\sim\mathcal{B}(0.5)\) independente și să definim \(X = BY\). Atunci funcția de repartiție a lui \(X\) verifică \(F(0-) = \frac{1}{4}\) și \(F(0) = \frac{3}{4}\), este injectivă dar nu și continuă în \(0\) și în plus avem \((F\circ F^{-1})(1/2) = F(0) = \frac{3}{4}>\frac{1}{2}\).

Se numește cuantilă de ordin \(p\in(0,1)\) (sau \(p\)-cuantilă) asociată lui \(F\) valoarea

\[ x_p = F^{-1}(p) = \inf\{x\in\mathbb{R}\,|\,F(x)\geq p\}. \]

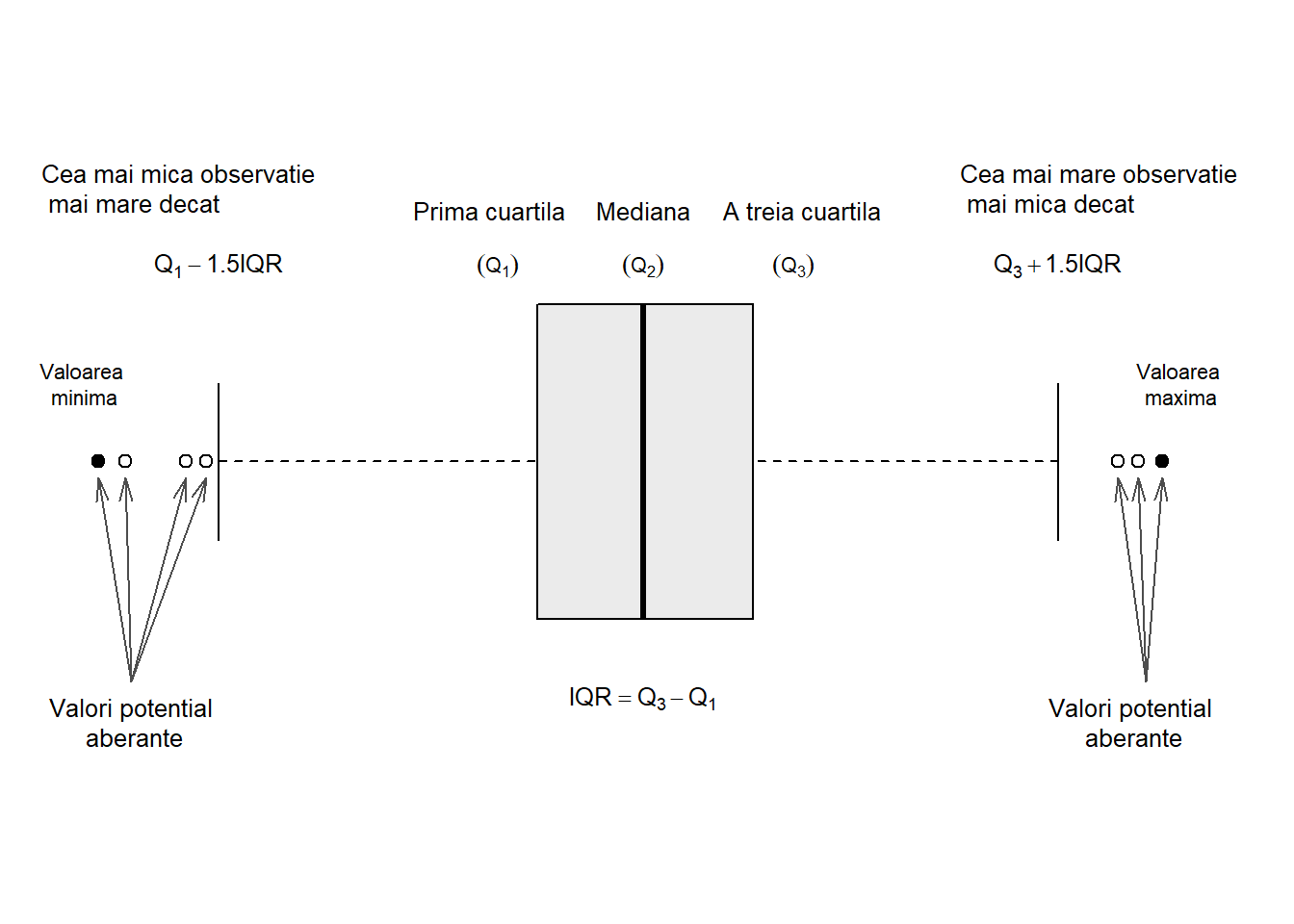
Cuantila de ordin \(0.5\), \(x_{\frac{1}{2}}\) se numește mediana lui \(F\) și se notează cu \(M\) sau \(Q_2\), iar cuantilele de ordin \(\frac{1}{4}\) și respectiv \(\frac{3}{4}\) se numesc prima și respectiv a treia cuartilă și se notează cu \(Q_1\) și respectiv \(Q_3\).

Fie acum \(X_1,X_2,\ldots,X_n\) un eșantion de talie \(n\) dintr-o populație a cărei funcție de repartiție este \(F\) și fie \(\hat{F}_n\) funcția de repartiție empirică asociată. Pentru \(p\in(0,1)\) definim cuantila empirică de ordin \(p\) și o notăm \(\hat{x}_p = \hat{x}_p(n)\) valoarea

\[ \hat{x}_p = \hat{F}_n^{-1}(p) = \inf\{x\in\mathbb{R}\,|\,\hat{F}_n(x)\geq p\}. \]

Folosind convenția \(X_{(0)}=-\infty\), cunatila empirică de ordin \(p\) coincide cu una dintre statisticile de ordine:

\[ \hat{x}_p = X_{(i)} \iff np\leq i< np+1 \iff \hat{x}_p = X_{(\lceil np \rceil)}, \]

unde \(\lceil x \rceil\) reprezintă cea mai mică valoare întreagă mai mare sau egală cu \(x\).

Are loc următorul rezultat³:

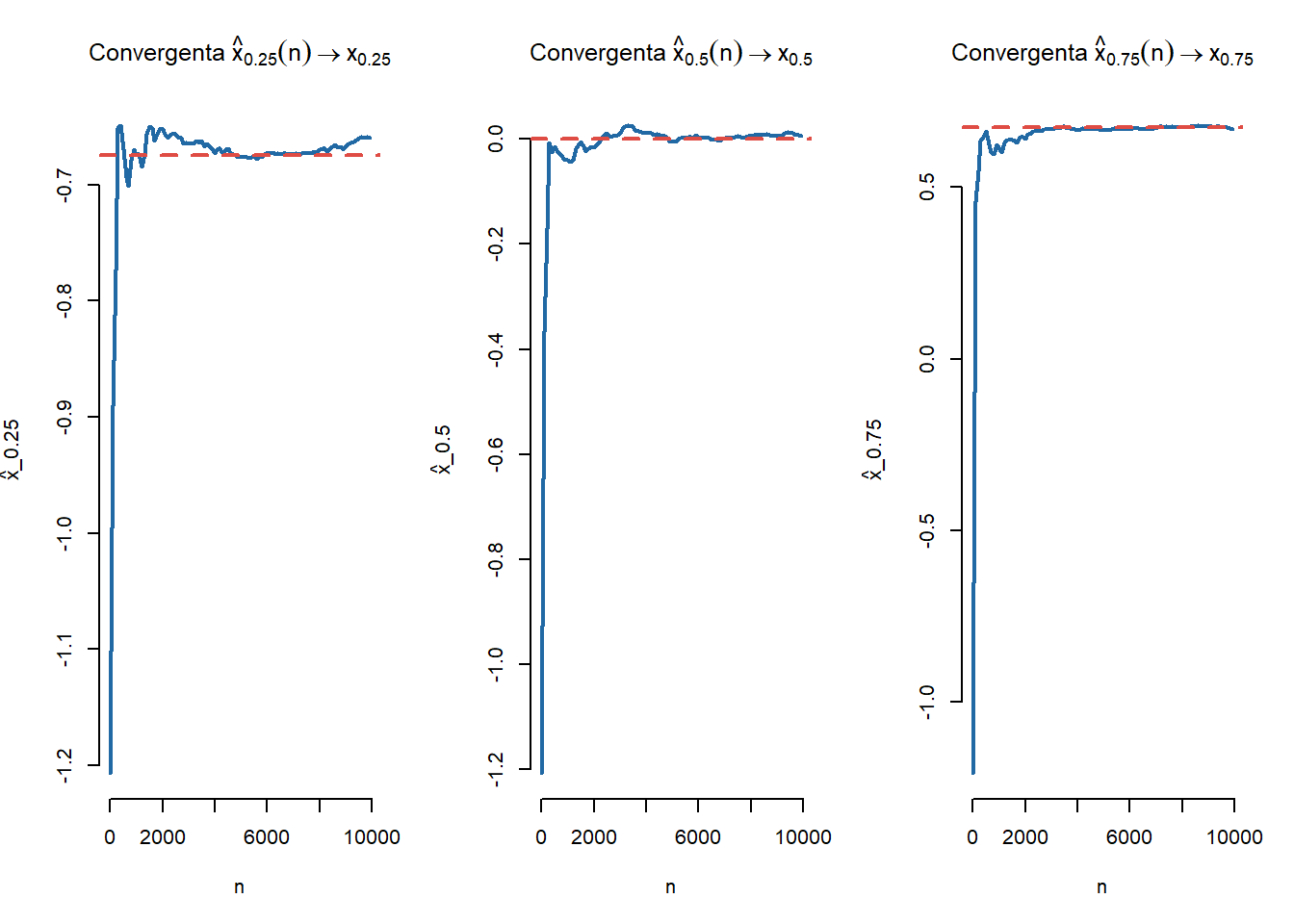
Teorema 7.1 (Convergența și normalitatea asimptotică a cuantilelor empirice) Fie \(X_1,X_2,\ldots,X_n\) un eșantion de talie \(n\) dintr-o populație cu funcția de repartiție \(F\), \(p\in(0,1)\) fixat, \(x_p\) cuantila de ordin \(p\) asociată lui \(F\) și \(\hat{x}_p(n)\) cuantila empirică de ordin \(p\). Atunci

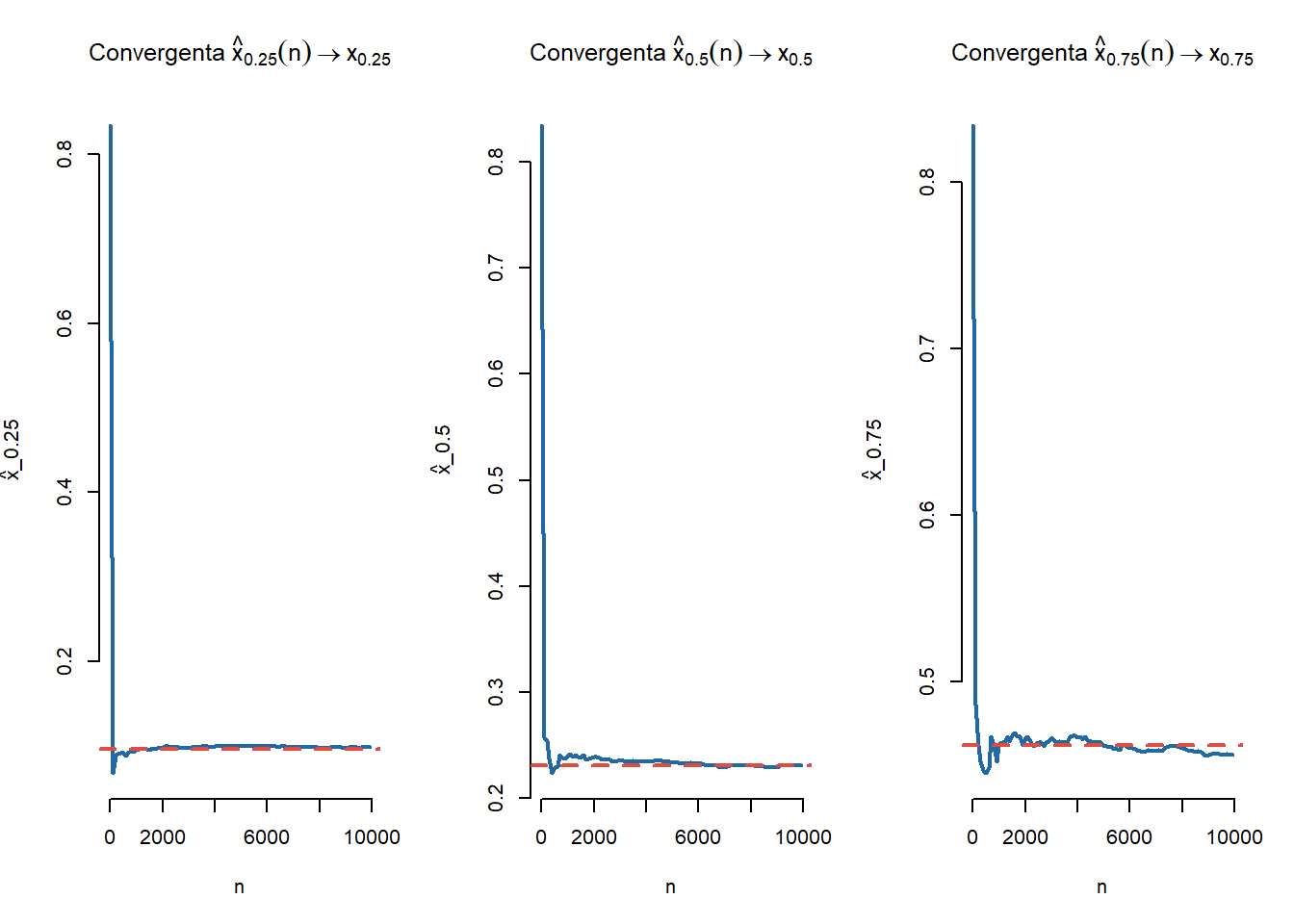
1. Convergența: dacă \(F\) este strict crescătoare în \(x_p\) are loc

\[ \hat{x}_p(n) \overset{a.s.}{\underset{n\to\infty}\longrightarrow} x_p \]

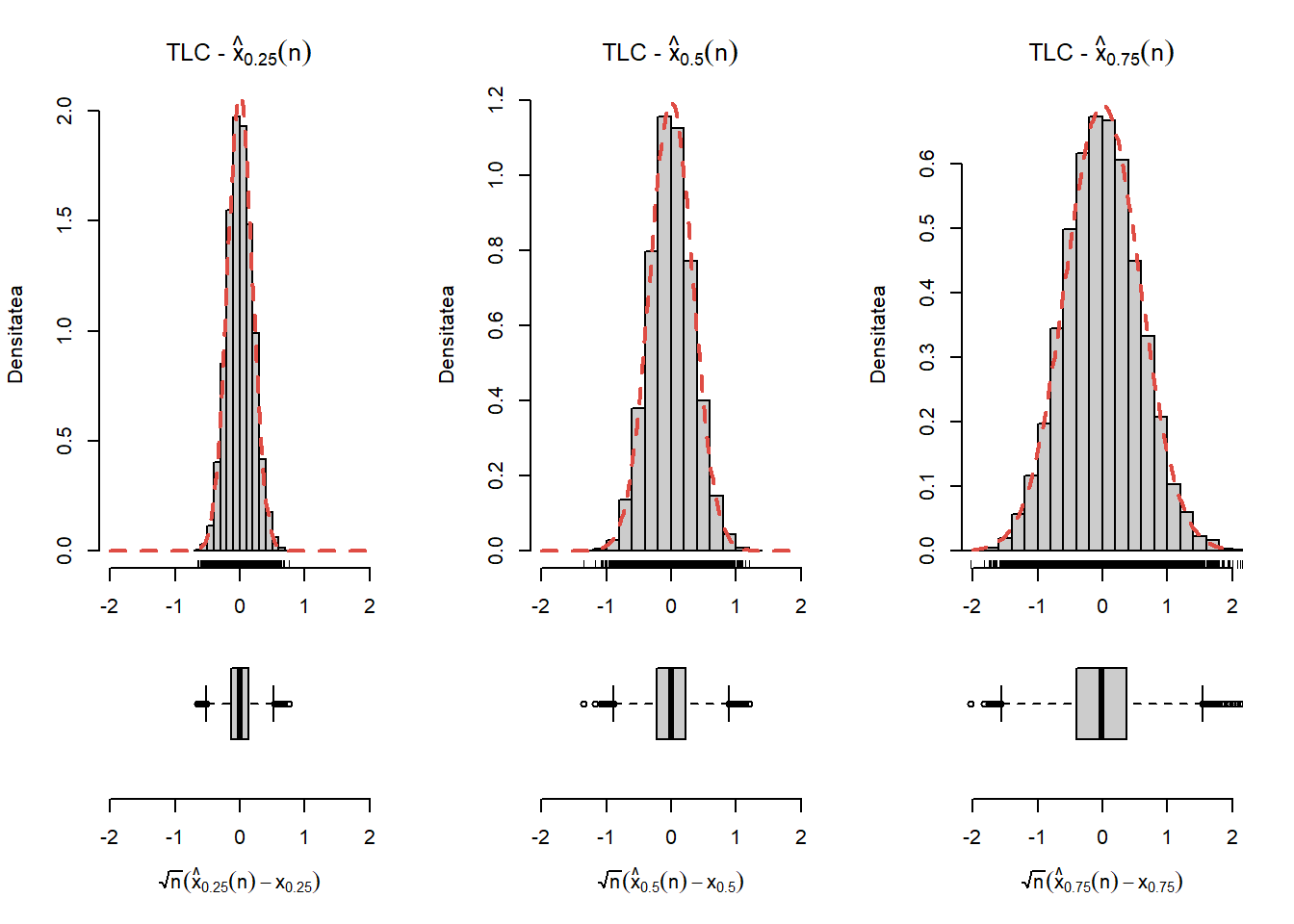
2. Normalitatea asimptotică: dacă \(F\) este derivabilă în \(x_p\) cu derivata \(f(x_p)>0\), atunci

\[ \sqrt{n}(\hat{x}_p(n) - x_p)\overset{d}{\underset{n\to\infty}\longrightarrow}\mathcal{N}\left(0,\frac{p(1-p)}{f(x_p)^2}\right). \]

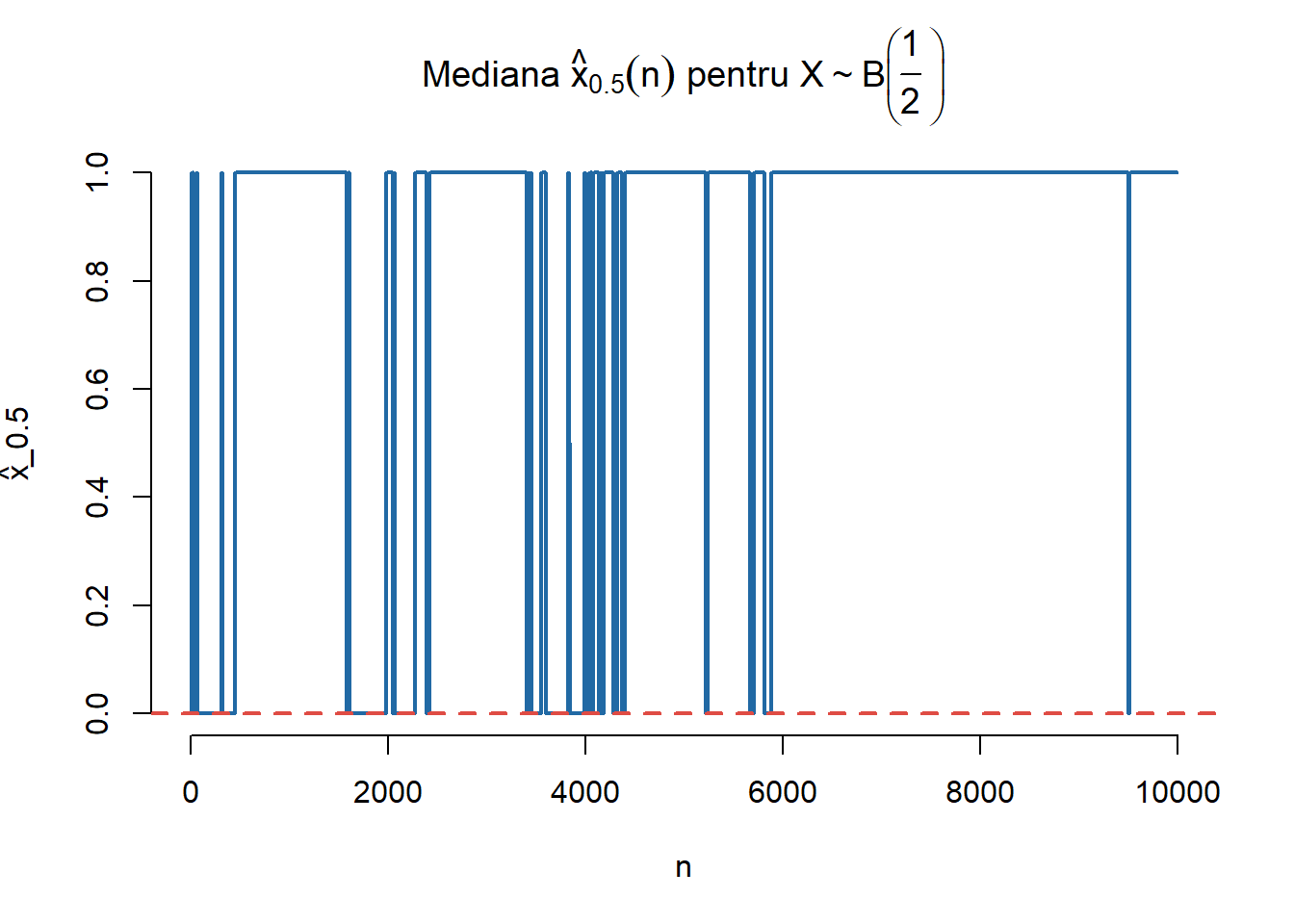
Pentru a ilustra importanța condiției de la primul punct (\(F\) este strict crescătoare în \(x_p\)) să considerăm \(X\sim\mathcal{B}(\frac{1}{2})\). Atunci mediana sa este \(x_{\frac{1}{2}} = 0\) pe când mediana empirică \(\hat{x}_{\frac{1}{2}}(n)\) va oscila mereu (dar neregulat) între valorile \(0\) și \(1\).

# Normala
N <- 10000
step <- 10

q2 <- qbinom(0.5, 1, 0.5)

n <- seq(1, N, step)

q2e <- rep(0, length(n))


set.seed(1234)
x <- rbinom(N, 1, 0.5)

for (i in seq_along(n)){
  y <- x[1:n[i]]
  q2e[i] <- quantile(y, probs = 0.5)
}

#-2
plot(n, q2e, type = "l",
     col = myblue,
     lty = 1,
     lwd = 2,
     bty = "n", 
     main = TeX("Mediana $\\hat{x}_{0.5}(n)$ pentru $X\\sim B\\left(\\frac{1}{2}\\right)$"),
     xlab = "n", 
     ylab = TeX("\\hat{x}_{0.5}"))

abline(h = q2, 
       col = myred, 
       lty = 2, 
       lwd = 2)

Figura 7.1: Ilustrarea încălcării condiției din convergență.

Exercițiul 7.1 Ilustrați grafic în R proprietatea de convergență și de normalitate asimptotică (din Teorema 7.1) pentru o populație repartizată \(\mathcal{N}(0,1)\) și respectiv \(\mathrm{Exp}(3)\) și pentru \(p\in\left\{\frac{1}{4}, \frac{1}{2}, \frac{3}{4} \right\}\).

Soluție. În cazul \(\mathcal{N}(0,1)\) avem proprietatea de convergență a cuantilelor

# Normala
N <- 10000
step <- 100

q1 <- qnorm(0.25)
q2 <- qnorm(0.5)
q3 <- qnorm(0.75)

n <- seq(1, N, step)

q1e <- rep(0, length(n))
q2e <- rep(0, length(n))
q3e <- rep(0, length(n))


set.seed(1234)
x <- rnorm(N)

for (i in seq_along(n)){
  y <- x[1:n[i]]
  
  q1e[i] <- quantile(y, probs = 0.25)
  q2e[i] <- quantile(y, probs = 0.5)
  q3e[i] <- quantile(y, probs = 0.75)
}

par(mfrow = c(1,3))
#-1
plot(n, q1e, type = "l",
     col = myblue,
     lty = 1,
     lwd = 2,
     bty = "n", 
     main = TeX("Convergenta $\\hat{x}_{0.25}(n) \\rightarrow x_{0.25}$"),
     xlab = "n", 
     ylab = TeX("\\hat{x}_{0.25}"))

# points(n, q1e, pch = 16,
#        col = myblue)

abline(h = q1, 
       col = myred, 
       lty = 2, 
       lwd = 2)
#-2
plot(n, q2e, type = "l",
     col = myblue,
     lty = 1,
     lwd = 2,
     bty = "n", 
     main = TeX("Convergenta $\\hat{x}_{0.5}(n) \\rightarrow x_{0.5}$"),
     xlab = "n", 
     ylab = TeX("\\hat{x}_{0.5}"))

# points(n, q2e, pch = 16,
#        col = myblue)

abline(h = q2, 
       col = myred, 
       lty = 2, 
       lwd = 2)
#-3
plot(n, q3e, type = "l",
     col = myblue,
     lty = 1,
     lwd = 2,
     bty = "n", 
     main = TeX("Convergenta $\\hat{x}_{0.75}(n) \\rightarrow x_{0.75}$"),
     xlab = "n", 
     ylab = TeX("\\hat{x}_{0.75}"))

# points(n, q3e, pch = 16,
#        col = myblue)

abline(h = q3, 
       col = myred, 
       lty = 2, 
       lwd = 2)

Figura 7.2: Ilustrarea proprietății de convergență a cuantilelor empirice în cazul \(\mathcal{N}(0,1)\).

și proprietatea de normalitate asimptotică

S <- 10000
n <- 1250

p1<- 0.25
p2 <- 0.5
p3 <- 0.75

q1 <- qnorm(p1)
q2 <- qnorm(p2)
q3 <- qnorm(p3)

fxp1 <- dnorm(q1)
fxp2 <- dnorm(q2)
fxp3 <- dnorm(q3)

sd1 <- sqrt(p1*(1-p1)/fxp1^2)
sd2 <- sqrt(p2*(1-p2)/fxp2^2)
sd3 <- sqrt(p3*(1-p3)/fxp3^2)

xp1n <- numeric(S) 
xp2n <- numeric(S) 
xp3n <- numeric(S) 

for (i in 1:S){
  x <- rnorm(n)
  xp1n[i] <- sqrt(n)*(quantile(x, p1) - q1)
  xp2n[i] <- sqrt(n)*(quantile(x, p2) - q2)
  xp3n[i] <- sqrt(n)*(quantile(x, p3) - q3)
}

par(mfrow = c(1, 3))

# plot 1 
par(fig = c(0, 1/3, 0, 0.45), bty = "n", new = T)
boxplot(xp1n, horizontal=T, bty="n",
        xlab = expression(sqrt(n) (hat(x)[0.25] (n) - x[0.25])),
        col = "grey80",
        ylim = c(-4, 4), 
        cex = 0.7)

par(fig = c(0, 1/3, 0.25, 1), new = T)
hist(xp1n, 
     probability = TRUE, 
     # breaks = seq(-4, 4, by = 0.5),
     xlim = c(-4, 4),
     col = "grey80",
     main = TeX("TLC - $\\hat{x}_{0.25}(n)$"),
     xlab = "",
     ylab = "Densitatea")

lines(seq(-4, 4, length.out = 250),
      dnorm(seq(-4, 4, length.out = 250), sd = sd1), 
      type = "l", 
      col = myred, lty = 2, lwd = 2)
rug(xp1n)

# plot 2 
par(fig = c(1/3, 2/3, 0, 0.45), bty = "n", new = T)
boxplot(xp2n, horizontal=T, bty="n", 
        xlab = expression(sqrt(n) (hat(x)[0.5] (n) - x[0.5])),
        col = "grey80",
        ylim = c(-4, 4), 
        cex = 0.7)

par(fig = c(1/3, 2/3, 0.25, 1), new = T)
hist(xp2n, 
     probability = TRUE, 
     # breaks = seq(-4, 4, by = 0.5),
     xlim = c(-4, 4),
     col = "grey80",
     main = TeX("TLC - $\\hat{x}_{0.5}(n)$"),
     xlab = "",
     ylab = "Densitatea")

lines(seq(-4, 4, length.out = 250),
      dnorm(seq(-4, 4, length.out = 250), sd = sd2), 
      type = "l", 
      col = myred, lty = 2, lwd = 2)
rug(xp2n)

# plot 3
par(fig = c(2/3, 1, 0, 0.45), bty = "n", new = T)
boxplot(xp3n, horizontal=T, bty="n", 
        xlab = expression(sqrt(n) (hat(x)[0.75] (n) - x[0.75])),
        col = "grey80",
        ylim = c(-4, 4), 
        cex = 0.7)

par(fig = c(2/3, 1, 0.25, 1), new = T)
hist(xp3n, 
     probability = TRUE, 
     # breaks = seq(-4, 4, by = 0.5),
     xlim = c(-4, 4),
     col = "grey80",
     main = TeX("TLC - $\\hat{x}_{0.75}(n)$"),
     xlab = "",
     ylab = "Densitatea")

lines(seq(-4, 4, length.out = 250),
      dnorm(seq(-4, 4, length.out = 250), sd = sd3), 
      type = "l", 
      col = myred, lty = 2, lwd = 2)
rug(xp3n)

Figura 7.3: Ilustrarea proprietății de normalitate asimptotică a cuantilelor empirice în cazul \(\mathcal{N}(0,1)\).

În cazul \(\mathrm{Exp}(3)\) avem proprietatea de convergență a cuantilelor

# Exponentiala
N <- 10000
step <- 100

q1 <- qexp(0.25, 3)
q2 <- qexp(0.5, 3)
q3 <- qexp(0.75, 3)

n <- seq(1, N, step)

q1e <- rep(0, length(n))
q2e <- rep(0, length(n))
q3e <- rep(0, length(n))


set.seed(1234)
x <- rexp(N, 3)

for (i in seq_along(n)){
  y <- x[1:n[i]]
  
  q1e[i] <- quantile(y, probs <- 0.25)
  q2e[i] <- quantile(y, probs <- 0.5)
  q3e[i] <- quantile(y, probs <- 0.75)
}

par(mfrow = c(1,3))
#-1
plot(n, q1e, type = "l",
     col = myblue,
     lty = 1,
     lwd = 2,
     bty = "n", 
     main = TeX("Convergenta $\\hat{x}_{0.25}(n) \\rightarrow x_{0.25}$"),
     xlab = "n", 
     ylab = TeX("\\hat{x}_{0.25}"))

# points(n, q1e, pch = 16,
#        col = myblue)

abline(h = q1, 
       col = myred, 
       lty = 2, 
       lwd = 2)
#-2
plot(n, q2e, type = "l",
     col = myblue,
     lty = 1,
     lwd = 2,
     bty = "n", 
     main = TeX("Convergenta $\\hat{x}_{0.5}(n) \\rightarrow x_{0.5}$"),
     xlab = "n", 
     ylab = TeX("\\hat{x}_{0.5}"))

# points(n, q2e, pch = 16,
#        col = myblue)

abline(h = q2, 
       col = myred, 
       lty = 2, 
       lwd = 2)
#-3
plot(n, q3e, type = "l",
     col = myblue,
     lty = 1,
     lwd = 2,
     bty = "n", 
     main = TeX("Convergenta $\\hat{x}_{0.75}(n) \\rightarrow x_{0.75}$"),
     xlab = "n", 
     ylab = TeX("\\hat{x}_{0.75}"))

# points(n, q3e, pch = 16,
#        col = myblue)

abline(h = q3, 
       col = myred, 
       lty = 2, 
       lwd = 2)

Figura 7.4: Ilustrarea proprietății de convergență a cuantilelor empirice în cazul \(\mathrm{Exp}(3)\).

și proprietatea de normalitate asimptotică

S <- 10000
n <- 1250

p1 <- 0.25
p2 <- 0.5
p3 <- 0.75

q1 <- qexp(p1, 3)
q2 <- qexp(p2, 3)
q3 <- qexp(p3, 3)

fxp1 <- dexp(q1, 3)
fxp2 <- dexp(q2, 3)
fxp3 <- dexp(q3, 3)

sd1 <- sqrt(p1*(1-p1)/fxp1^2)
sd2 <- sqrt(p2*(1-p2)/fxp2^2)
sd3 <- sqrt(p3*(1-p3)/fxp3^2)

xp1n <- numeric(S) 
xp2n <- numeric(S) 
xp3n <- numeric(S) 

for (i in 1:S){
  x <- rexp(n, 3)
  xp1n[i] <- sqrt(n)*(quantile(x, p1) - q1)
  xp2n[i] <- sqrt(n)*(quantile(x, p2) - q2)
  xp3n[i] <- sqrt(n)*(quantile(x, p3) - q3)
}

par(mfrow = c(1, 3))

# plot 1 
par(fig = c(0, 1/3, 0, 0.45), bty = "n", new = T)
boxplot(xp1n, horizontal=T, bty="n", 
        xlab = expression(sqrt(n) (hat(x)[0.25] (n) - x[0.25])),
        col = "grey80",
        ylim = c(-2, 2), 
        cex = 0.7)

par(fig = c(0, 1/3, 0.25, 1), new = T)
hist(xp1n, 
     probability = TRUE, 
     # breaks = seq(-4, 4, by = 0.5),
     xlim = c(-2, 2),
     col = "grey80",
     main = TeX("TLC - $\\hat{x}_{0.25}(n)$"),
     xlab = "",
     ylab = "Densitatea")

lines(seq(-2, 2, length.out = 250),
      dnorm(seq(-2, 2, length.out = 250), sd = sd1), 
      type = "l", 
      col = myred, lty = 2, lwd = 2)
rug(xp1n)

# plot 2 
par(fig = c(1/3, 2/3, 0, 0.45), bty = "n", new = T)
boxplot(xp2n, horizontal=T, bty="n", 
        xlab = expression(sqrt(n) (hat(x)[0.5] (n) - x[0.5])),
        col = "grey80",
        ylim = c(-2, 2), 
        cex = 0.7)

par(fig = c(1/3, 2/3, 0.25, 1), new = T)
hist(xp2n, 
     probability = TRUE, 
     # breaks = seq(-4, 4, by = 0.5),
     xlim = c(-2, 2),
     col = "grey80",
     main = TeX("TLC - $\\hat{x}_{0.5}(n)$"),
     xlab = "",
     ylab = "Densitatea")

lines(seq(-2, 2, length.out = 250),
      dnorm(seq(-2, 2, length.out = 250), sd = sd2), 
      type = "l", 
      col = myred, lty = 2, lwd = 2)
rug(xp2n)

# plot 3
par(fig = c(2/3, 1, 0, 0.45), bty = "n", new = T)
boxplot(xp3n, horizontal=T, bty="n", 
        xlab = expression(sqrt(n) (hat(x)[0.75] (n) - x[0.75])),
        col = "grey80",
        ylim = c(-2, 2), 
        cex = 0.7)

par(fig = c(2/3, 1, 0.25, 1), new = T)
hist(xp3n, 
     probability = TRUE, 
     # breaks = seq(-4, 4, by = 0.5),
     xlim = c(-2, 2),
     col = "grey80",
     main = TeX("TLC - $\\hat{x}_{0.75}(n)$"),
     xlab = "",
     ylab = "Densitatea")

lines(seq(-2, 2, length.out = 250),
      dnorm(seq(-2, 2, length.out = 250), sd = sd3), 
      type = "l", 
      col = myred, lty = 2, lwd = 2)
rug(xp3n)

Figura 7.5: Ilustrarea proprietății de normalitate asimptotică a cuantilelor empirice în cazul \(\mathrm{Exp}(3)\).

Metode grafice

Diagrama cu bare (barplot)

Diagrama cu batoane sau bare (barplot) este o metodă grafică folosită cu precădere atunci când datele sunt discrete (date calitative). O diagramă de tip barplot trasează bare verticale sau orizontale, în general separate de un spațiu alb, pentru a evidenția frecvențele de apariție a observațiilor după categoriile corespunzătoare.

Să presupunem că \(X\) este o variabilă aleatoare discretă cu funcția de masă dată de \(p(x)=\mathbb{P}(X = x)\) și \(X_1, X_2, \ldots, X_n\) un eșantion de volum \(n\) din populația \(p(x)\). Dacă \(X\) ia un număr finit de valori, \(X\in\mathcal{A}\) cu \(\mathcal{A} = \{a_1, \ldots, a_m\}\), atunci un estimator nedeplasat și consistent al lui \(p(a_j)\) este

\[ \hat{p}(a_j) = \frac{1}{n}\sum_{i = 1}^{n}\mathbf{1}_{\left\{X_i = a_j\right\}}. \]

Dacă \(X\) ia un număr infinit (numărabil) de valori, \(X\in\mathcal{A}\) cu \(\mathcal{A} = \{a_1, a_2, \ldots\}\), atunci putem să formăm grupurile

\[ \{a_1\}, \;\{a_2\},\cdots, \{a_m\},\; \tilde{a}_{m+1} = \{a_{m+1}, a_{m+2}, \ldots\} \]

și să considerăm

\[ \hat{p}(\tilde{a}_{m+1}) = \frac{1}{n}\sum_{i = 1}^{n}\mathbf{1}_{\left\{X_i \geq a_{m+1}\right\}}. \] În practică, alegerea lui \(m\) se face așa încât \(\hat{p}(a_m)\geq 2\hat{p}(\tilde{a}_{m+1})\). O diagramă cu bare este o ilustrare a lui \(a_j\) versus \(\hat{p}(a_j)\).

În R, diagrama cu bare se ilustrează prin intermediul funcției barplot().

Exercițiul 8.1 Folosind setul de date mtcars ilustrați prin intermediul unei diagrame cu bare greutatea medie a mașinilor din setul de date în funcție de numărul de cilindrii.

Soluție. Avem următorul cod R:

par(mfrow = c(1, 2))

weight_cars <- aggregate(wt ~ cyl, 
                        data = mtcars, 
                        FUN = mean)

barplot(height = weight_cars$wt,
        names.arg = weight_cars$cyl,
        xlab = "Numar de cilindrii",
        ylab = "Greutatea medie",
        main = "Greutatea medie dupa numarul de cilindrii\n Barplot vertical",
        col = "grey80", 
        cex.main = 0.7)

barplot(height = weight_cars$wt,
        names.arg = weight_cars$cyl,
        horiz = TRUE,
        ylab = "Numar de cilindrii",
        xlab = "Greutatea medie",
        main = "Greutatea medie dupa numarul de cilindrii\n Barplot orizontal",
        col = "grey80", 
        cex.main = 0.7)

Figura 8.1: Greutatea medie a mașinilor după numărul de cilindrii: diagramă cu bare verticală și orizontală.

Dacă în plus vrem să afișăm greutatea medie a mașinilor din setul de date în funcție atât de numărul de cilindrii cât și de tipul de transmisie avem următorul cod R:

# calculam greutatea medie dupa numarul de cilindrii si transmisie 
carWeight_cyl_am <- aggregate(mtcars$wt, 
                              by = list(mtcars$cyl, mtcars$am), 
                              FUN = mean) 

# transformam rezultatul sub forma de matrice
carWeight_cyl_am <- as.matrix(carWeight_cyl_am)

# aducem la forma necesara pentru barplot
carWeight <- matrix(carWeight_cyl_am[,3], nrow = 3)
colnames(carWeight) <- unique(carWeight_cyl_am[,2])
rownames(carWeight) <- unique(carWeight_cyl_am[, 1])

carWeight <- t(carWeight)

barplot(carWeight, 
        beside = TRUE,
        legend.text = TRUE, 
        args.legend = list(x = "topleft", 
                           bty = "n"),
        col = c(myblue, myred),
        main = "Greutatea medie a masinilor dupa numarul de cilindrii si transmisie",
        cex.main = 0.8,
        xlab = "Numar de cilindrii",
        ylab = "Greutatea medie")

Figura 8.2: Greutatea medie a mașinilor după numărul de cilindrii și tipul de transmisie.

Histograma

Histograma este un exemplu de metodă neparametrică de estimare a densității de probabilitate. Fie \(X_1, X_2, \ldots, X_n\) un eșantion de volum \(n\) dintr-o populație cu densitate de probabilitate \(f\). Fără a restrânge generalitatea putem să presupunem că \(X_i\in[0,1]\) (în caz contrar putem scala observațiile la acest interval).

Fie \(m\) un număr natural și să considerăm diviziunea intervalului \([0,1]\) (fiecare subinterval din diviziune se numește bin):

\[ B_1 = \left[0, \frac{1}{m}\right), \, B_2 = \left[\frac{1}{m}, \frac{2}{m}\right),\cdots,\, B_m = \left[\frac{m-1}{m}, 1\right]. \]

Notăm cu \(h = \frac{1}{m}\) lungimea intervalelor din diviziune (a bin-urilor), \(p_j = \mathbb{P}(X_i\in B_j) = \int_{B_j}f(t)\,dt\) probabilitatea ca o observație să se afle în subintervalul \(B_j\) și \(\hat{p}_j = \frac{1}{n}\sum_{i = 1}^{n}\mathbf{1}_{\left\{X_i \in B_j\right\}}\) numărul de observații, din cele \(n\), care se află în intervalul \(B_j\). Observăm că \(\hat{p}_j\) este un estimator nedeplasat și consistent pentru \(p_j\).

Atunci estimatorul histogramă este dat de

\[ \hat{f}_n(x) = \left\{\begin{array}{llll} \frac{\hat{p}_1}{h}, & x\in B_1\\ \frac{\hat{p}_2}{h}, & x\in B_2\\ \vdots, & \vdots\\ \frac{\hat{p}_m}{h}, & x\in B_m \end{array}\right. \]

care scris sub formă compactă devine

\[ \hat{f}_n(x) = \sum_{i=1}^{m} \frac{\hat{p}_i}{h} \mathbf{1}_{B_i}(x). \]

Se poate observa că pentru \(m\) suficient de mare (\(h\) mic) și \(x\in B_j\) avem

\[ \mathbb{E}\left[\hat{f}_n(x)\right] = \mathbb{E}\left[\sum_{i=1}^{m} \frac{\hat{p}_i}{h} \mathbf{1}_{B_i}(x)\right]= \frac{\mathbb{E}\left[\hat{p}_j\right]}{h} = \frac{p_j}{h} = \frac{\int_{B_j}f(x)\,dx}{h}\approx \frac{f(x)h}{h} = f(x). \]

Alegerea numărului de bin-uri și a mărimii acestora nu este o problemă trivială. De exemplu, D. Scott propune o variantă de alegere a lui \(m\) în articolul (Scott 1979). Un rezultat similar, dar mai robust, a fost obținut de D. Freedman și P. Diaconis în (Freedman and Diaconis 1981). Câteva dintre metodele de alegere a mărimii bin-ului sunt prezentate în următoarea pagină de Wikipedia.

În R, funcția hist() este folosită pentru trasarea unei histograme. Această funcție utilizează ca metodă predefinită de alegere a mărimii bin-urilor, metoda lui Sturges (a se vedea articolul (Sturges 1926)), i.e. \(m = \lceil \log_2(n)\rceil + 1\).

Exercițiul 8.2 Considerați setul de date mtcars. Investigați cu ajutorul unei histograme cum este repartizată variabila hp. Trasați prin drepte verticale de culori diferite media și respectiv mediana datelor.

Soluție. Următorul cod R implementează cerința problemei:

par(mfrow = c(1,2))

hist(mtcars$hp, freq = FALSE,
     main = "Horepower - HP\n (default)", 
     xlab="HP")

hist(mtcars$hp, freq = FALSE,
     breaks=seq(0,400,25),
     col="gray",
     main="Horsepower - HP\n (marimea bin-ului 25)",
     xlab="HP")

abline(v=c(mean(mtcars$hp), median(mtcars$hp)), 
       lty=c(2,3), lwd=2)
legend("topright", legend=c("media HP","mediana HP"),
       lty=c(2,3), lwd=2,
       bty = "n")

Figura 8.3: Repartiția variabilei hp.

Exercițiul 8.3 Să presupunem că în fișierul studFMI.txt am stocat date privind sexul (f/h), înălțimea (în cm) și greutatea (în kg) a studenților de master de la Facultatea de Matematică și Informatică. Vrem să investigăm, trasând pe același grafic, cum este repartizată înălțimea și respectiv greutatea studenților în funcție de sex.

Soluție. Începem prin a citi datele din fișier:

stud <- read.table("../dataIn/studFMI.txt", header = TRUE)
str(stud)

'data.frame':   97 obs. of  3 variables:
 $ sex   : chr  "h" "h" "f" "f" ...
 $ height: int  168 177 164 166 165 150 186 185 181 188 ...
 $ weight: int  69 73 53 57 60 42 74 83 77 72 ...

head(stud)

  sex height weight
1   h    168     69
2   h    177     73
3   f    164     53
4   f    166     57
5   h    165     60
6   f    150     42

Separăm înălțimea (greutatea este exercițiu!) bărbaților și a femeilor:

# h vine de la hommes iar f de la femmes
hm <- stud$height[stud$sex == "h"]
hf <- stud$height[stud$sex == "f"]

par(mfrow = c(1,2))

hist(hm, freq = FALSE, col = grey(0.8),
     main = "Inaltimea barbatilor", 
     xlab = "inaltimea",
     ylab = "densitatea")
tm = seq(min(hm)-5, max(hm)+5, length.out = 100)
lines(tm, dnorm(tm, mean(hm), sd(hm)), 
      lty = 2, lwd = 2)

hist(hf, freq = FALSE, col = grey(0.8),
     main = "Inaltimea femeilor", 
     xlab = "inaltimea",
     ylab = "densitatea")
tf = seq(min(hf)-5, max(hf)+5, length.out = 100)
lines(tf, dnorm(tf, mean(hf), sd(hf)), 
      lty = 2, lwd = 2)

Figura 8.4: Repartiția înălțimii studenților de sex masculin și feminin în setul de date.

Reprezentăm repartiția înălțimilor luate împreună și evidențiem mixtura celor două repartiții după sex:

height <- stud$height

hist(height, proba = TRUE, 
     breaks=25, 
     col = grey(0.8), 
     main = "Inaltimea barbatilor si a femeilor",
     xlab = "inaltimea",
     ylab = "densitatea",
     ylim = c(0, 0.05))

t <- seq(145,200,length=100)

x1 <- dnorm(t,mean(hf),sd(hf))
x2 <- dnorm(t,mean(hm),sd(hm))

# proportia de femei (din nr de studenti)
pf <- length(hf)/length(height)

# mixtura dintre rep inaltimilor f si h
x3 <- pf*x1 + (1-pf)*x2

lines(t, x3, lwd = 2)

lines(t, pf*x1, col = myred, 
      lty = 2, lwd = 2)
lines(t, (1-pf)*x2, col = myblue, 
      lty = 2, lwd = 2)

legend("topright", c("femei","barbati"), 
       col = c(myred,myblue), 
       lty = 2, lwd = 2, 
       bty = "n")

Figura 8.5: Repartiția studenților după înălțime și evidențierea mixturii celor două repartiții după sex.

Boxplot-ul

Una dintre metodele grafice des întâlnite în vizualizarea datelor (cantitative) unidimensionale este boxplot-ul (eng. box and whisker plot - cutia cu mustăți). Această metodă grafică descriptivă este folosită în principal pentru a investiga atât forma repartiției (simetrică sau asimetrică) datelor cât și variabilitatea acestora precum și pentru detectarea și ilustrarea schimbărilor de locație și variație între diferitele grupuri de date.

După cum putem vedea și în Figura 8.6 de mai jos, cutia este definită, de la stânga la dreapta (sau de jos în sus în funcție de cum este reprezentat boxplot-ul: orizontal sau vertical), de prima cuartilă \(Q_1\) și de a treia curatilă \(Q_3\) ceea ce înseamnă că \(50\%\) dintre observații se află în interiorul cutiei. Linia din interiorul cutiei este determinată de mediană sau a doua cuartilă \(Q_2\).

Mustățile care pornesc de o parte și de alta a cutiei sunt determinate astfel (vom folosi convenția folosită de John Tukey în (J. 1977, pag. 40-56)): mustața din stânga este determinată de cea mai mică observație mai mare decât \(Q_1-1.5 IQR\) iar cea din dreapta de cea mai mare observație din setul de date mai mică decât \(Q_3+1.5IQR\), unde \(IQR = Q_3-Q_1\) este distanța dintre cuartile (interquartile range).

Valorile observațiilor din setul de date care sunt sau prea mici sau prea mari se numesc valori aberante (outliers) și conform lui Tukey sunt definite astfel: valori strict aberante care se află la \(3IQR\) deasupra celei de-a treia curtilă \(Q_3\) sau la \(3IQR\) sub prima cuartilă (\(x<Q_1-3IQR\) sau \(x>Q_3+3IQR\)) și valori potențial aberante care se află la \(1.5IQR\) deasupra celei de-a treia curtilă \(Q_3\) sau la \(1.5IQR\) sub prima cuartilă (\(x<Q_1-1.5IQR\) sau \(x>Q_3+1.5IQR\)).

Figura 8.6: Diagramă ilustrativă a unui boxplot.

În R metoda grafică boxplot se poate trasa cu ajutorul funcției boxplot(). Aceasta primește ca argumente sau un vector de observații numerice x, atunci când dorim să ilustrăm repartiția unei variabile, sau o formulă de tipul y~grup, unde y este un vector numeric care va fi împărțit în funcție de variabila discretă grup, atunci când vrem să comparăm aceeași variabilă numerică în funcție de una discretă (calitativă). Pentru mai multe informații puteți consulta documentația funcției, i.e. ?boxplot.

Exercițiul 8.4 Considerați setul de date mtcars. Investigați cu ajutorul unui boxplot cum variază greutatea mașinilor, variabila wt, în funcție de numărul de cilindrii cyl. Afișați numele mașinilor care prezintă potențiale valori aberante. Aceeași cerință pentru perechile mpg - cyl, hp - cyl și hp - am.

Soluție. Vom ilustra codul R pentru prima cerință, celelalte fiind similare:

par(bty = "n")
bp <- boxplot(mtcars$wt ~ mtcars$cyl,
             xlab = "Numar de cilindrii", 
             ylab = "Greutate (in tone)",
             col = "grey80",
             main = "Setul de date mtcars: greutate vs numar cilindrii")

cars <- mtcars[mtcars$cyl == 8, ]
cars.names <- rownames(cars)[which(cars$wt %in% bp$out)]

text(c(3,3,2.4)+0.3, bp$out, cars.names, cex = 0.6)
text( c(1:length(unique(mtcars$cyl))) , 
      bp$stats[nrow(bp$stats) , ] + 0.5 , 
      paste("n = ", table(mtcars$cyl),sep=""),
      cex = 0.8)

Figura 8.7: Greutatea mașinilor în funcție de numărul de cilindrii.

Numele mașinilor care au o greutate potențial aberantă este Cadillac Fleetwood, Lincoln Continental, Chrysler Imperial.

Graficul de tip cuantilă-cuantilă

Graficul de tip cuantilă-cuantilă (quantile-quantile plot sau q-q plot pe scurt) este o metodă grafică introdusă în (Wilk and Gnanadesikan 1968) și folosită pentru a determina dacă două eșantioane provin din populații cu repartiție comună. Un q-q plot ilustrează grafic cuantilele empirice ale primului eșantion față de cuantilele empirice (sau teoretice) ale celui de-al doilea eșantion.

Fiind date două eșantioane, \(X_1,X_2,\ldots,X_n\sim F\) și respectiv \(Y_1, Y_2, \ldots, Y_m\sim G\), fie \(\hat{x}_p(n) = \hat{F}_n^{-1}(p)\) și \(\hat{y}_p(m) = \hat{G}_m^{-1}(p)\) cuantilele empirice de ordin \(p\) asociate celor două eșantioane. Metoda q-q plot implică trasarea pe același grafic al punctelor de coordonate \((\hat{x}_p(n), \hat{y}_p(m))\) pentru diverse valori ale lui \(p\in(0,1)\). După cum am văzut în Capitolul 7, cunatila empirică de ordin \(p\) coincide cu una dintre statisticile de ordine \(\hat{x}_p = X_{(i)} \iff \hat{x}_p = X_{(\lceil np \rceil)}\) (deci \(X_{(k)}\) este cuantila de ordin \(\frac{k}{n}\)) și prin urmare putem considera că

\[ p\in \left\{\begin{array}{ll} \left\{\frac{i}{n}\,|\,1\leq i\leq n\right\}, & n\leq m\\ \left\{\frac{i}{m}\,|\,1\leq i\leq m\right\}, & n\geq m. \end{array}\right. \] În practică, pentru a avea \(p<1\) vom considera că \(X_{(k)}\) este cuantila de ordin \(\frac{k}{n+1}\) (unii autori consideră că \(X_{(k)}\) este cuantila de ordin \(\frac{k-0.5}{n}\) sau încă de ordin \(\frac{k-3/8}{n+1/4}\)), astfel

\[ p\in \left\{\begin{array}{ll} \left\{\frac{i}{n+1}\,|\,1\leq i\leq n\right\}, & n\leq m\\ \left\{\frac{i}{m+1}\,|\,1\leq i\leq m\right\}, & n\geq m. \end{array}\right. \]

În R putem folosi funcția qqplot() pentru a trasa graficul cuantilă-cuantilă (tastați ?qqplot pentru a vedea documentația acestei funcții).

Exercițiul 8.5 Construiți în R o funcție qqgraf() care să traseze graficul cuantilă-cuantilă pentru două eșantioane.

Soluție. Următorul cod R implementează această funcție:

qqgraf <- function(x, y, line = TRUE,
                  type = "1",
                  xlab = deparse(substitute(x)), 
                  ylab = deparse(substitute(y)), ...){
  sx <- sort(x)
  sy <- sort(y)
  
  lenx <- length(sx)
  leny <- length(sy)
  
  len <- ifelse(lenx>leny, leny, lenx)
  
  if (type == "1"){
      p = 1:len/(len+1)
    }else if(type == "2"){
      p = (1:len - 0.5)/len
    }else{
      p = (1:len - 3/8)/(len+1/4)
    }
  
  qx <- quantile(x, probs = p)
  qy <- quantile(y, probs = p)
  
  plot(qx, qy, 
       pch = 21, 
       bg = grey(0.8, 0.8),
       bty = "n", 
       xlab = xlab, 
       ylab = ylab,
       ...)
  # abline(a = mean(y)-mean(x), b = sd(y)/sd(x))
  
  if (line == TRUE)
    abline(a = 0, b = 1, lwd = 2, 
           lty = 2, col = myred)
  
}

Observăm că dacă cele două eșantioane ar proveni de la aceeași populație (\(F = G\)) atunci punctele ar fi aliniate aproximativ pe o dreaptă (prima bisectoare \(y=x\)).

x <- rnorm(100)
y <- rnorm(150)

qqgraf(x, y)

Figura 8.8: Ilustrarea graficului cuantilă-cuantilă pentru două eșantioane provenite dintr-o populație normală.

O deviere de la prima bisectoare indică o diferență între formele celor două repartiții din care au provenit datele. Atunci când cele două repartiții au aceeași formă dar au medii și respectiv abateri standard diferite atunci graficul rămâne liniar numai că ordonata la origine și panta dreptei nu vor mai fi \(0\) și respectiv \(1\). O ordonată la origine diferită de \(0\) arată o translatare în repartiții (schimbare de locație) iar o pantă neunitară indică o schimbare de scală.

par(mfrow = c(1,2))

x <- rnorm(200, 2, 1)
y <- rnorm(150)

qqgraf(x, y, main = "Translatare")
abline(a = -2, b = 1, 
       col = "grey80", 
       lty = 2, lwd = 2)

x <- rnorm(200, 0, 2)
y <- rnorm(150)

qqgraf(x, y, main = "Scalare")
abline(a = 0, b = 1/2, 
       col = "grey80",
       lty = 2, lwd = 2)

Figura 8.9: Evidențierea fenomenului de translație și respectiv scalare în graficul cuantilă-cuantilă.

Graficul cuantilă-cuantilă poate fi folosit și pentru a verifica dacă un eșantion provine dintr-o repartiție specificată, astfel, dat fiind \((X_1, X_2, \ldots, X_n)(\omega) = (x_1, x_2, \ldots, x_n)\) un eșantion de volum \(n\) vrem să verificăm dacă acesta provine dintr-o populație (specificată) \(F\). Dacă \(\hat{x}_p(n)\) este cuantila empirică de ordin \(p\) și \(x_p = F^{-1}(p)\) este cuantila teoretică de ordin \(p\) asociată lui \(F\), atunci graficul cuantilă-cuantilă este determinat de punctele \(\left(x_p,\hat{x}_p(n)\right)\), \(p\in(0,1)\). Folosind alegerea lui \(p\) de mai sus (care evită singularitățile \(F^{-1}(1) = \infty\)) și ținând cont că \(\hat{x}_{\frac{i}{n+1}}(n) = X_{(i)}\) avem că graficul cuantilă-cuantilă este determinat de mulțimea de puncte

\[ \mathcal{G} = \left\{\left(F^{-1}\left(\frac{i}{n+1}\right), X_{(i)}\right)\,|\, 1\leq i\leq n\right\}. \]

Pentru a verifica dacă datele provin dintr-o repartiție normală este suficient să alegem \(F = \Phi\), cu \(\Phi(x)\) funcția de repartiție a normalei standard (acest grafic se mai numește și normal probability plot sau normal-quantile plot). Dacă punctele se află (aproximativ) pe o dreaptă atunci putem spune că datele provin dintr-o repartiție (aproximativ) normală. Deplasarea față de normalitate este indicată prin deplasarea față de o dreaptă. Un grafic în formă de U arată că repartiția este asimetrică iar un grafic în formă de S ne spune că avem diferențe între coada repartiției normale și cea care a generat setul de date.

În R putem trasa graficul cuantilă-cuantilă pentru o populație normală cu ajutorul funcției qqnorm() iar dreapta de referință cu ajutorul funcției qqline(). Pentru mai multe detalii privind aceste funcții tastați ?qqnorm și ?qqline.

Exercițiul 8.6 Construiți în R o funcție qq_norm() care să traseze graficul cuantilă-cuantilă (normal-quantile plot) pentru a verifica dacă un eșantion provine dintr-o populație normală.

Soluție. Codul funcției qq_norm() este dat mai jos:

qq_norm <- function(x, line = TRUE,
                   type = "1", 
                   xlab = "Cuantile teoretice", 
                   ylab = "Cuantile empirice", ...){
  
  sx <- sort(x)
  lenx <- length(sx)
  
  if (type == "1"){
      p <- 1:lenx/(lenx+1)
    }else if(type == "2"){
      p <- (1:lenx - 0.5)/lenx
    }else{
      p <- (1:lenx - 3/8)/(lenx+1/4)
    }
  
  qx <- quantile(x, probs = p)
  qy <- qnorm(p)
  
  plot(qy, qx, 
       pch = 21, 
       bg = grey(0.8, 0.8),
       bty = "n", 
       xlab = xlab, 
       ylab = ylab,
       ...)

  if (line == TRUE){
    xq <- quantile(x[!is.na(x)], c(0.25, 0.75))
    xn <- qnorm(c(0.25, 0.75))
    
    slope <- diff(xq)/diff(xn)
    int <- xq[1]-slope*xn[1]
    abline(a = int, b = slope, lwd = 2, 
           lty = 2, col = myred)
  }
}

Apelând această funcție putem vizualiza ce se întâmplă în situația în care eșantionul provine dintr-o repartiție cu coadă scurtă, coadă lungă sau asimetrică.

par(mfrow = c(2,2))
n <- 250

# coada scurta 
x_st <- runif(n, min=0, max=2)
qq_norm(x_st, main = "Coada scurta")

# coada lunga 
x_ht <- rcauchy(n, location=0, scale=1)
qq_norm(x_ht, main = "Coada lunga")

# asimetrica spre stanga 
x_sn <- rbeta(n, 2, 0.5, ncp = 2)
qq_norm(x_sn, main = "Asimetrica spre stanga")

# asimetrica spre dreapta 
x_sp <- rexp(n, 2)
qq_norm(x_sp, main = "Asimetrica spre dreapta")

Figura 8.10: Graficul cuantilă-cuantilă pentru diverse scenarii.

Exercițiul 8.7 Considerați setul de date birthwt din pachetul MASS. Trasați histograma greutății la naștere a copiilor (variabila bwt) și graficul cuantilă-cuantilă pentru o populație normală. Comparați grafic dacă repartiția greutății copiilor la naștere diferă în funcție de statutul de fumător al mamei.

Soluție. Repartiția eșantionului peste care am suprapus densitatea normală corespunzătoare, împreună cu graficul cuantilă-cuantilă sunt ilustrate de codul R următor:

par(mfrow = c(1,2), 
    cex.main = 0.8,
    cex.axis = 0.7,
    cex.lab = 0.7)

hist(birthwt$bwt, 
     probability = TRUE, 
     col = "grey80",
     main = "Repartitia greutatii",
     xlab = "Greutatea la nastere",
     ylab = "Densitate")

t <- seq(min(birthwt$bwt), max(birthwt$bwt), 
        length.out = 100)
x <- dnorm(t, mean(birthwt$bwt), sd(birthwt$bwt))

lines(t, x, lwd = 2, lty = 2,
      col = myred)

qq_norm(birthwt$bwt, 
        main = "Graficul cuantila-cuantila")

Figura 8.11: Histograma greutății la naștere a copiilor și graficul cuantilă-cuantilă corespunzător.

Greutatea la naștere a copiilor din setul de date în funcție de statutul de fumător al mamei este evidențiat mai jos:

par(mfrow = c(2,2),
     cex.main = 0.8,
     cex.axis = 0.7,
     cex.lab = 0.7)

bwt_nf <- birthwt$bwt[birthwt$smoke == 0]
bwt_f <- birthwt$bwt[birthwt$smoke == 1]
bwt <- birthwt$bwt

# nefumatoare
hist(bwt_nf, proba = TRUE,
      breaks=25,
      col = grey(0.8),
      main = "Greutatea copiilor\n (mame nefumatoare)",
      xlab = "Greutatea la nastere",
      ylab = "densitatea",
      ylim = c(0, 6e-4))

t_nf <- seq(min(bwt_nf), max(bwt_nf), 
        length.out = 100)

x_nf <- dnorm(t_nf, mean(bwt_nf), sd(bwt_nf))

lines(t_nf, x_nf, col = myred,
      lty = 2, lwd = 2)

qq_norm(bwt_nf,
        main = "Graficul cuantila-cuantila")

# fumatoare
hist(bwt_f, proba = TRUE,
      breaks=25,
      col = grey(0.8),
      main = "Greutatea copiilor\n (mame fumatoare)",
      xlab = "Greutatea la nastere",
      ylab = "densitatea",
      ylim = c(0, 6e-4))

t_f <- seq(min(bwt_nf), max(bwt_nf), 
        length.out = 100)

x_f <- dnorm(t_f, mean(bwt_f), sd(bwt_f))

lines(t_f, x_f, col = myred,
      lty = 2, lwd = 2)

qq_norm(bwt_f,
        main = "Graficul cuantila-cuantila")

Figura 8.12: Repartiția greutății copiilor la naștere în funcție de statutul de fumător al mamei.

Ce se întâmplă atunci când avem o mixtură de repartiții? Următoarea funcție permite generarea unui eșantion dintr-o mixtură de două repartiții normale:

\[ f(x) = p\frac{1}{\sqrt{2\pi\sigma_1^2}}e^{-\frac{1}{2}\left(\frac{x-\mu_1}{\sigma_1}\right)^2} + (1-p)\frac{1}{\sqrt{2\pi\sigma_2^2}}e^{-\frac{1}{2}\left(\frac{x-\mu_2}{\sigma_2}\right)^2}, \; p\in (0,1) \]

mix_norm_sim <- function(n = 100, p = 0.5, m1 = -1, sd1 = 1, m2 = 2, sd2 = 2){
  n1 <- rbinom(1,n,p)
  x1 <- rnorm(n1, m = m1, sd = sd1)
  x2 <- rnorm(n-n1, m = m2, sd = sd2)
  c(x1, x2)
}

Ilustrăm grafic metoda cuantilă-cuantilă pentru diferite scenarii:

par(mfrow=c(2,2),
     cex.main = 0.8,
     cex.axis = 0.7,
     cex.lab = 0.7)
#----------
w0 = mix_norm_sim(1000,0.25,-20,10,20,10)
hist(w0, col = grey(0.8),
     probability = TRUE,
     main = "Scenariul 1", 
     xlab = "Observatii", 
     ylab = "Densitatea")
qq_norm(w0, main = "Q-Q plot - Scenariul 1")
#----------
w1 = mix_norm_sim(1000,0.5,0,1,5,1)
hist(w1, col = grey(0.8),
     probability = TRUE,
     main = "Scenariul 2", 
     xlab = "Observatii", 
     ylab = "Densitatea")
qq_norm(w1, main = "Q-Q plot - Scenariul 2")

Figura 8.13: Graficul cuantilă-cuantilă în cazul unei mixturi de normale.

Referințe

Freedman, D., and P. Diaconis. 1981. “On the Histogram as a Density Estimator: \(L_2\) Theory.” Z. Wahrscheinlichkeitstheorie Verw. Gebiete 57: 453–76.

Gill, D. N. Joanes; C. A. 1998. “Comparing Measures of Sample Skewness and Kurtosis.” Journal of the Royal Statistical Society: Series D (The Statistician) 47: 183–89. https://doi.org/10.1111/1467-9884.00122.

J., Tukey. 1977. Exploratory Data Analysis. Addison-Wesley Publishing Company.

Scott, D. 1979. “On Optimal and Data-Based Histograms.” Biometrika 66: 605–10.

Sturges, H. 1926. “The Choice of a Class Interval.” Journal of the American Statistical Association 65.

Wilk, M. B., and R. Gnanadesikan. 1968. “Probability Plotting Methods for the Analysis of Data.” Biometrika 55: 1–17. https://doi.org/10.2307/2334448.

Note de subsol

1. În esență vom folosi următoarea proprietate: Fie \(U\) și \(V\) doi vectori aleatori și \(f_{(U,V)}(u,v)\) densitatea comună a vectorului comun \((U,V)\). Dacă există \(g\) și \(h\) astfel încât \(f_{(U,V)}(u,v) = g(u)h(v)\) pentru orice \(u\) și \(v\), atunci \(U\) și \(V\) sunt independenți.

2. Pentru o demonstrație a acestei teoreme se poate consulta, spre exemplu, cartea lui Sidney Resnick A probability path, Springer, 1998 (pag 224)

3. O demonstrație a acestui rezultat care nu necesită funcții caracteristice se regăsește în articolul lui Jan Wretman A Simple Derivation of the Asymptotic Distribution of a Sample Quantile, Scand. J. Statist., 5(2): 123-124, 1978.