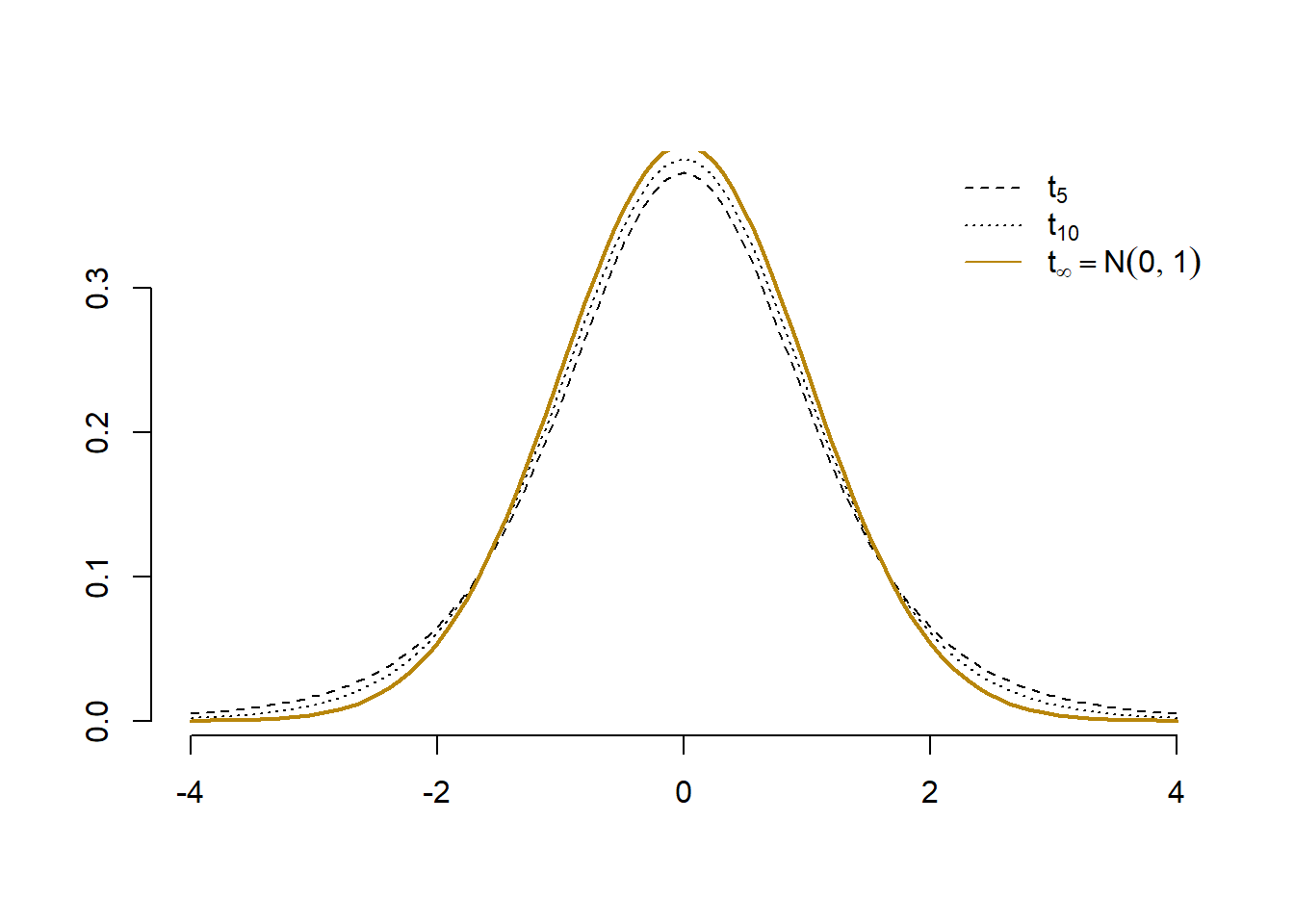Repartiții derivate din repartiția normală
În afară de repartiția normală, următoarele trei repartiții sunt des utilizate în inferența statistică a modelului clasic de regresie liniară: repartiția \(\chi^2\), repartiția Student \(t\) și repartiția Fisher-Snedecor \(F\).
Repartiția \(\chi^2\)
Definiția 1 (Variabilă aleatoare repartizată \(\chi^2(n)\)) Spunem că o variabilă aleatoare \(X\) este repartizată \(\chi^2\) (Hi-pătrat) cu \(n\) grade de libertate și se notăm cu \(X\sim \chi^2(n)\) (sau încă \(X\sim \chi^2_n\)) dacă admite densitatea de repartiție
\[ f(x)=\frac{1}{2^{n / 2} \Gamma\left(\frac{n}{2}\right)} x^{n / 2-1} e^{-x / 2} \mathbf{1}_{\{x>0\}} \]
unde \(\Gamma(\cdot)\) este funcția Gamma dată de \(\Gamma(x)=\int_{0}^{\infty} u^{x-1} \mathrm{e}^{-u} \mathrm{d} u, x>0\).
Următoarele două propoziții caracterizează repartiția \(\chi^2(n)\).
Propoziția 1 Arătați că dacă \(X\sim \mathcal{N}(0, 1)\) atunci \(Y=X^2\sim\chi^2(1)\).
Demonstrație. Să observăm pentru început că dacă \(y<0\) atunci
\[ F_Y(y) = \mathbb{P}(Y\leq y) = \mathbb{P}(X^2\leq y) = 0. \]
Pentru \(y\geq 0\) avem
\[ \begin{aligned} F_Y(y) & =\mathbb{P}\left(X^2 \leq y\right)=\mathbb{P}(|X| \leq \sqrt{y}) \\ & =\mathbb{P}(-\sqrt{y} \leq X \leq \sqrt{y})=\Phi(\sqrt{y})-\Phi(-\sqrt{y})=\Phi(\sqrt{y})-(1-\Phi(\sqrt{y})) \\ & =2 \Phi(\sqrt{y})-1 \end{aligned} \]
de unde găsim că
\[ \begin{aligned} f_Y(y) & =2 \frac{d}{d y} \Phi(\sqrt{y})=2 \frac{d}{d \sqrt{y}} \Phi(\sqrt{y}) \frac{d}{d y} \sqrt{y} \\ & =2 \phi(\sqrt{y}) \frac{y^{-1 / 2}}{2}=2 \frac{1}{\sqrt{2 \pi}} e^{-y / 2} \frac{y^{-1 / 2}}{2} \\ & =\frac{1}{\sqrt{2} \sqrt{\pi}} e^{-y / 2} y^{-1 / 2}=\frac{1}{2^{1 / 2} \Gamma(1 / 2)} y^{1 / 2-1} e^{-y / 2} \end{aligned} \]
ceea ce arată că \(Y\sim\chi^2(1)\).
Propoziția 2 (Rezultat de caracterizare a repartiției \(\chi^2(n)\)) Dacă \(X_1,\ldots,X_n\) sunt variabile aleatoare i.i.d. repartizate \(\mathcal{N}(0, 1)\) atunci variabila aleatoare \(X = \sum_{i = 1}^{n}X_i^2\) este repartizată \(\chi^2(n)\).
Demonstrație. Vom arăta pentru început că dacă \(X\sim \chi^2(n)\) iar \(Y\sim \chi^2(m)\) cu \(X\) și \(Y\) independente atunci
\[ X + Y \sim \chi^2(n + m). \]
Știm că dacă \(X\sim f_{X}\), \(Y\sim f_{Y}\) și \(X\) și \(Y\) independente atunci densitatea sumei \(X+Y\) este dată de
\[ f_{X+Y}(z) = \int_{-\infty}^{\infty}f_{X}(z - y)f_{Y}(y)\,dy \]
de unde, înlocuind \(f_X\) și \(f_Y\) cu densitățile \(\chi^2\) corespunzătoare, găsim că
\[ \begin{aligned} f_{X+Y}(z) &= \int_{-\infty}^{\infty}\frac{1}{2^{n / 2} \Gamma\left(\frac{n}{2}\right)} (z-y)^{n / 2-1} e^{-(z-y) / 2} \mathbf{1}_{\{z-y>0\}}\frac{1}{2^{m / 2} \Gamma\left(\frac{m}{2}\right)} y^{m / 2-1} e^{-y / 2} \mathbf{1}_{\{y>0\}}\,dy\\ &= \frac{1}{2^{\frac{n+m}{2}} \Gamma\left(\frac{n}{2}\right)\Gamma\left(\frac{m}{2}\right)}\int_{0}^{z}(z-y)^{n / 2-1} e^{-(z-y) / 2}y^{m / 2-1} e^{-y / 2}\,dy\\ &= \frac{e^{-z / 2}}{2^{\frac{n+m}{2}} \Gamma\left(\frac{n}{2}\right)\Gamma\left(\frac{m}{2}\right)}\int_{0}^{z}(z-y)^{n / 2-1} y^{m / 2-1} \,dy\\ &= \frac{e^{-z / 2}}{2^{\frac{n+m}{2}} \Gamma\left(\frac{n}{2}\right)\Gamma\left(\frac{m}{2}\right)}z^{\frac{n+m}{2}-2}\int_{0}^{z}\left(1-\frac{y}{z}\right)^{n / 2-1} \left(\frac{y}{z}\right)^{m / 2-1} \,dy\\ &\stackrel{t=\frac{y}{z}}{=} \frac{e^{-z / 2}}{2^{\frac{n+m}{2}} \Gamma\left(\frac{n}{2}\right)\Gamma\left(\frac{m}{2}\right)}z^{\frac{n+m}{2}-2}\int_{0}^{1}\left(1-t\right)^{n / 2-1} t^{m / 2-1} z\,dt\\ &= \frac{e^{-z / 2}}{2^{\frac{n+m}{2}} \Gamma\left(\frac{n}{2}\right)\Gamma\left(\frac{m}{2}\right)}z^{\frac{n+m}{2}-1}B\left(\frac{m}{2}, \frac{n}{2}\right) \end{aligned} \]
Folosind identitatea \(B\left(\frac{m}{2}, \frac{n}{2}\right) = \frac{\Gamma\left(\frac{n+m}{2}\right)}{\Gamma\left(\frac{n}{2}\right)\Gamma\left(\frac{m}{2}\right)}\) găsim
\[ f_{X+Y}(z) = \frac{1}{2^{\frac{n+m}{2}} \Gamma\left(\frac{n+m}{2}\right)}z^{\frac{n+m}{2}-1}e^{-z / 2}\mathbf{1}_{\{z>0\}} \]
ceea ce arată că \(X + Y \sim \chi^2(n+m)\).
Am văzut în propoziția anterioară că dacă \(X_i\sim\mathcal{N}(0, 1)\) atunci \(X_i^2\sim\chi^2(1)\). Cum \(X_1,\ldots,X_n\) sunt variabile aleatoare i.i.d. repartizate \(\mathcal{N}(0, 1)\) rezultă că \(X_1^2,\ldots,X_n^2\) sunt variabile aleatoare i.i.d. repartizate \(\chi^2(1)\). Aplicând identitatea sumei de mai sus pentru variabile \(\chi^2\) independente obținem concluzia.
Alternativ, acest rezultat se poate demonstra ușor folosind noțiunea de funcție generatoare de moment. De exemplu, funcția generatoare de moment pentru \(X\sim\chi^2(n)\) este dată de
\[ \begin{aligned} M_X(t) &= \mathbb{E}\left[e^{t X}\right] =\int_0^{\infty} e^{t x} f_{X}(x) \,d x \\ & =\frac{1}{2^{n / 2} \Gamma\left(\frac{n}{2}\right)} \int_0^{\infty} e^{t x} \cdot x^{n / 2-1} e^{-x/2}\, d x \\ & =\frac{1}{2^{n / 2} \Gamma\left(\frac{n}{2}\right)} \int_0^{\infty} x^{n / 2-1} e^{\left(t-\frac{1}{2}\right) x} d x. \end{aligned} \]
Aceasta este definită pentru \(t<\frac{1}{2}\) și folosind schimbare de variabilă \(s = \left(\frac{1}{2} - t\right)x\) avem
\[ \begin{aligned} M_X(t) & =\frac{1}{2^{n / 2} \Gamma\left(\frac{n}{2}\right)} \int_0^{\infty} x^{n / 2-1} e^{\left(t-\frac{1}{2}\right) x} d x\\ & =\left(\frac{1}{2}-t\right)^{-n / 2} \frac{1}{2^{n / 2} \Gamma\left(\frac{n}{2}\right)} \int_0^{\infty} s^{n / 2-1} e^{-s} d s \\ & =(1-2 t)^{-n / 2} \underbrace{\frac{1}{\Gamma\left(\frac{n}{2}\right)} \int_0^{\infty} s^{n / 2-1} e^{-s} d s}_{=1}\\ & =(1-2 t)^{-n / 2} . \end{aligned} \]
Din ipoteză avem că \(X = \sum_{i = 1}^{n}X_i^2\), unde \(X_i^2\) sunt variabile aleatoare independente repartizate \(\chi^2(1)\) prin urmare \(M_{X_i^2}(t) = (1-2 t)^{-1 / 2}\). Știm că funcția generatoare de moment a unei sume de variabile aleatoare independente este egală cu produsul funcțiilor generatoare de moment, astfel
\[ \begin{aligned} M_X(t) & = \prod_{i=1}^n M_{X_i}(t) = \prod_{i=1}^n (1-2 t)^{-1 / 2} = (1-2 t)^{-n / 2} \end{aligned} \]
ceea ce arată că funcția generatoare de moment a lui \(X\) coincide cu cea a repartiției \(\chi^2(n)\). Din teorema de unicitate a funcțiilor generatoare de moment avem concluzia.
Media și varianța sunt date de propoziția următoare:
Propoziția 3 Pentru o v.a. \(X\sim \chi^2(n)\) avem că \(\mathbb{E}[X] = n\) și \(Var(X) = 2n\).
Demonstrație. Într-adevăr, ținând cont că \(X = \sum_{i = 1}^{n}X_i^2\), cu \(X_i\sim\mathcal{N}(0, 1)\), și că \(\mathbb{E}\left[X_i^2\right]=1\) avem că
\[ \mathbb{E}\left[\chi^2(n)\right]=\mathbb{E}\left[\sum_{i=1}^n X_i^2\right]=\sum_{i=1}^n \mathbb{E}\left[X_i^2\right]=n \]
iar din independență și din faptul că \(Var\left(X_i^2\right)=\mathbb{E}\left[X_i^4\right] - \mathbb{E}\left[X_i^2\right]^2 = 3- 1 = 2\) găsim că
\[ Var\left(\chi^2(n)\right) = Var\left(\sum_{i=1}^n X_i^2\right) = \sum_{i=1}^n Var\left(X_i^2\right)=2n. \]
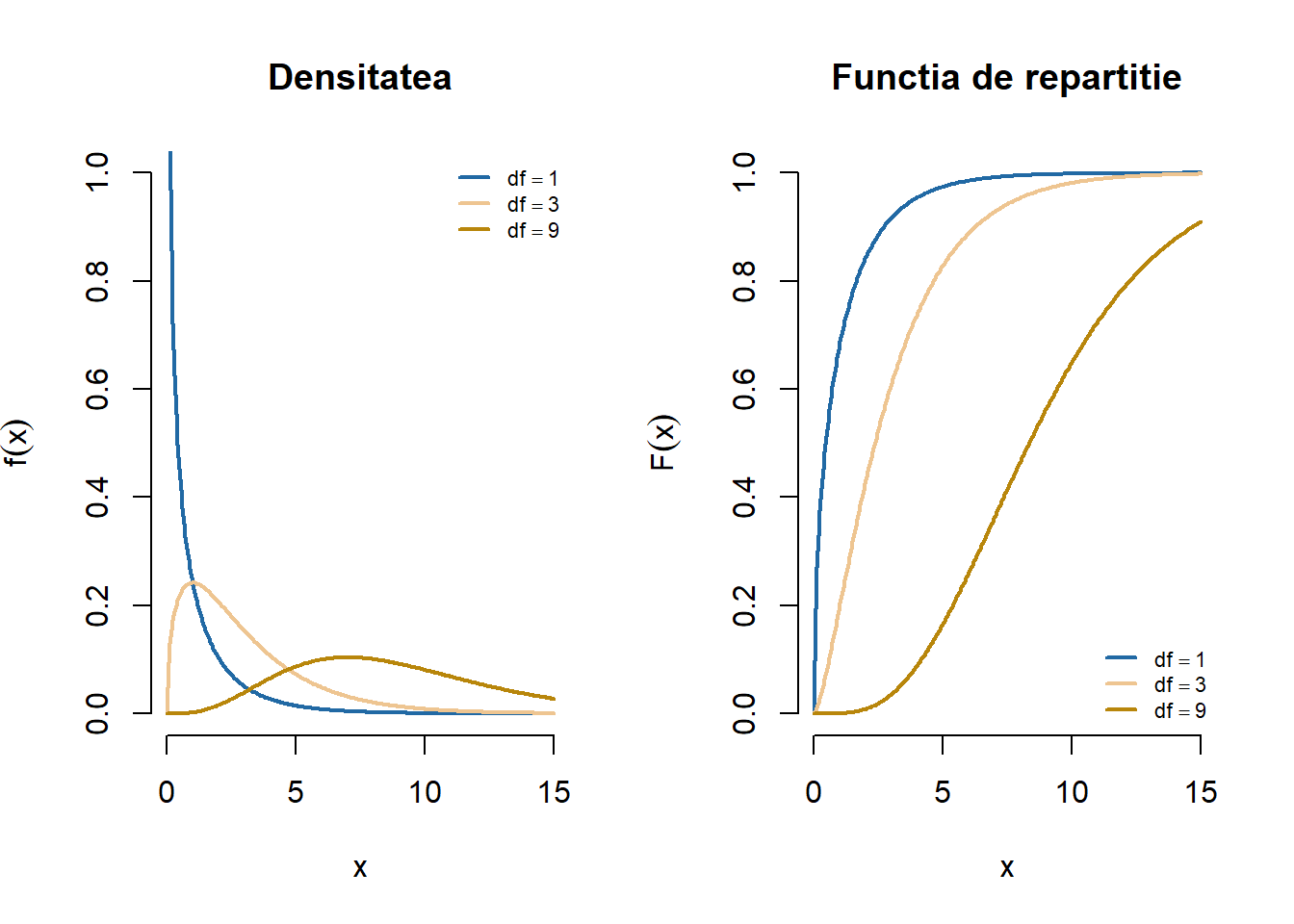
Figura 1 de mai jos ilustrează densitatea și funcția de repartiție a unei variabile aleatoare repartizată \(\chi^2(n)\) unde \(n\in\{1, 3, 9\}\).
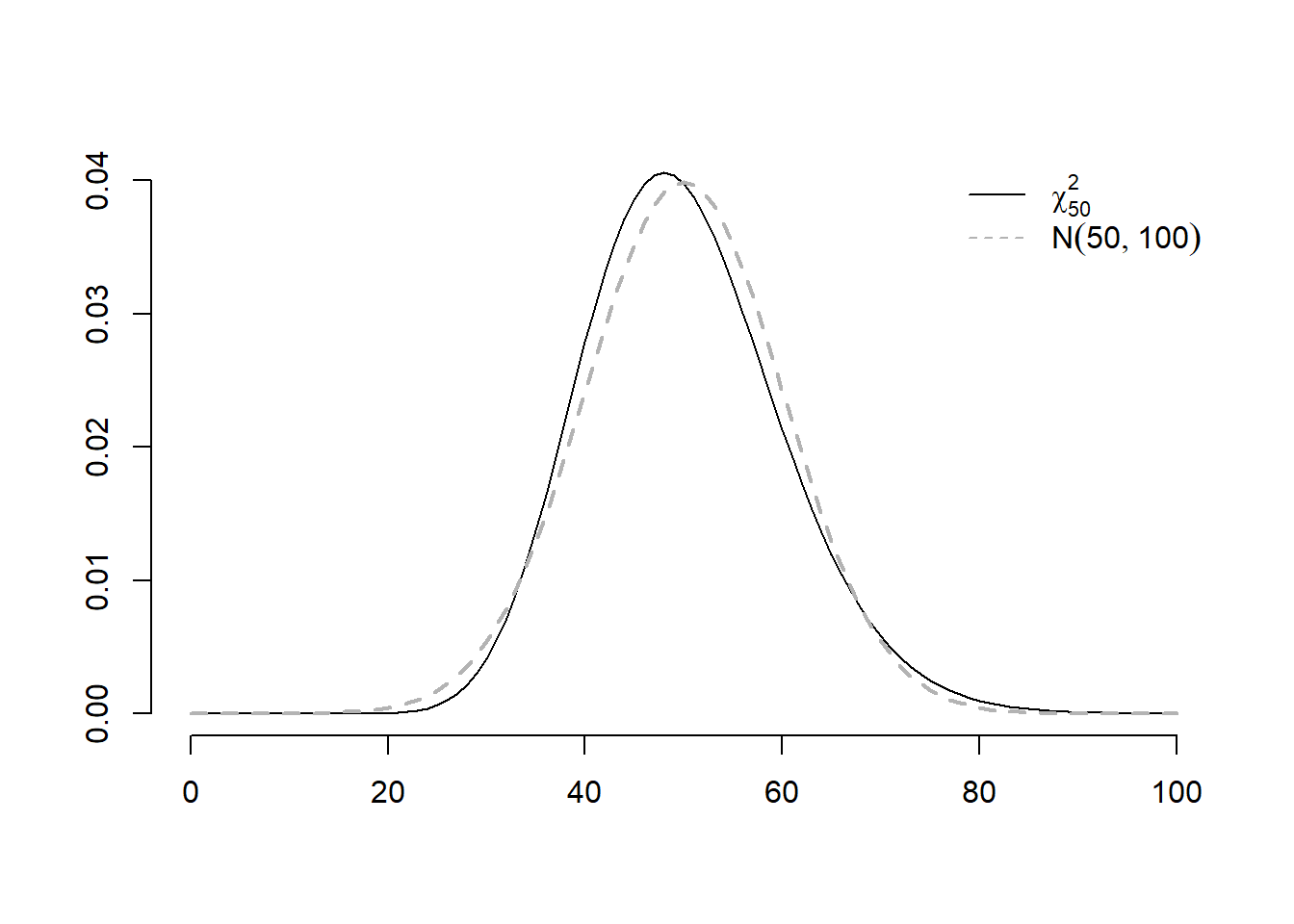
Din Teorema Limită Centrală avem că pentru \(n\) suficient de mare, \(X\approx \mathcal{N}(n, 2n)\) ceea ce sugerează că aproximativ \(95\%\) dintre valori se situează în intervalul \([n - 2\sqrt{2n}, n + 2\sqrt{2n}]\).
Repartiția \(t\)-Student
Repartiția Student sau t-Student este numită după un autor care a publicat în revista Biometrika în anul 1908 un articol care făcea referire la această repartiție sub pseudonimul Student. În realitate, cel care a publicat articolul era William Sealy Gosset.
Definiția 2 (Variabilă aleatoare repartizată Student) Spunem că variabila aleatoare \(T\) este repartizată Student cu \(n\) grade de libertate și notăm cu \(T\sim t_n\) (sau încă \(T\sim t(n)\)) dacă \(T\) admite densitatea de repartiție
\[ f_n(x)=\frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{\pi n}\Gamma\left(\frac{n}{2}\right)}\left(1+\frac{x^{2}}{n}\right)^{-\frac{n+1}{2}},\, x \in \mathbb{R} \]
Avem următorul rezultat:
Propoziția 4 (Rezultat de caracterizare a repartiției Student) Fie \(U\) o variabilă aleatoare repartizată \(\mathcal{N}(0, 1)\) și \(V\) o variabilă repartizată \(\chi^2(n)\), cu \(U\) și \(V\) independente, atunci variabila aleatoare \(T = \frac{U}{\sqrt{\frac{V}{n}}}\) este repartizată Student cu \(n\) grade de libertate.
Demonstrație. Vom determina pentru început repartiția comună a vectorului \((T, V)\) și, plecând de la aceasta, vom găsi repartiția marginală a lui \(T\). În acest sens considerăm transformarea
\[ g:(u, v) \mapsto(t, v)=\left(\frac{u}{\sqrt{v /n}}, v\right) \]
astfel că \((T,V) = g(U, V)\) și a cărei inversă este dată de
\[ g^{-1}:(t, v) \mapsto\left(t \sqrt{\frac{v}{n}}, v\right). \]
Matricea Jacobiană corespunzătoare lui \(g^{-1}\) este
\[ J_{g^{-1}}=\left(\begin{array}{cc} \sqrt{v /n} & t \frac{1}{2 \sqrt{v}\sqrt{n}} \\ 0 & 1 \end{array}\right) \]
de unde găsim determinantul \(\operatorname{det}\left(J_{g^{-1}}(t, v)\right)=\sqrt{\frac{v}{n}}\). Cum \(U\) și \(V\) sunt independente rezultă că densitatea comună a vectorului \((U,V)\) este
\[ f_{U, V}(u, v)=f_U(u) f_V(v)=\frac{1}{\sqrt{2\pi}}e^{-\frac{u^2}{2}}\frac{1}{2^{\frac{n}{2}} \Gamma\left(\frac{n}{2}\right)} v^{\frac{n}{2}-1} e^{-\frac{v}{2}} \]
prin urmare densitatea comună a vectorului \((T,V)\) este
\[ \begin{aligned} f_{T, V}(t, v) & =f_{U, V}\left(g^{-1}(t, v)\right)\left|\operatorname{det}\left(J_{g-1}(t, v)\right)\right|=f_{U, V}\left(t \sqrt{\frac{v}{n}}, v\right) \sqrt{\frac{v}{n}}\\ & =\frac{1}{2^{\frac{n}{2}} \sqrt{2\pi} \Gamma\left(\frac{n}{2}\right)} v^{\frac{n}{2}-1} e^{-\frac{1}{2}\left(v+v \frac{t^2}{n}\right)} \cdot\sqrt{\frac{v}{n}} \\ & =\frac{1}{2^{\frac{n}{2}} \sqrt{2\pi n} \Gamma\left(\frac{n}{2}\right)} \cdot v^{\frac{n+1}{2}-1} e^{-\frac{v}{2}\left(1+\frac{t^2}{n}\right)} . \end{aligned} \]
Densitatea marginală a lui \(T\) este
\[ f_T(t)=\frac{1}{2^{\frac{n}{2}} \sqrt{2\pi n} \Gamma\left(\frac{n}{2}\right)} \int_0^{\infty} e^{-\frac{v}{2}\left(\frac{t^2}{n}+1\right)} v^{\frac{n+1}{2}-1} d v \]
și considerând schimbarea de variabilă \(y = \frac{v}{2}\left(\frac{t^2}{n}+1\right)\) găsim \(v = \frac{2y}{\frac{t^2}{n}+1}\) de unde \(d v = \frac{2}{\frac{t^2}{n}+1} d y\) ceea ce conduce la
\[ \begin{aligned} f_T(t) & =\frac{1}{2^{\frac{n}{2}} \sqrt{2\pi n} \Gamma\left(\frac{n}{2}\right)} \cdot \int_0^{\infty} e^{-y} \cdot\left[(2 y)\left(\frac{t^2}{n}+1\right)^{-1}\right]^{\frac{n+1}{2}-1} \cdot 2\left(\frac{t^2}{n}+1\right)^{-1} d y \\ & =\frac{1}{2^{\frac{n}{2}} \sqrt{2\pi n} \Gamma\left(\frac{n}{2}\right)} \cdot\frac{2^{\frac{n+1}{2}}}{\left(\frac{t^2}{n}+1\right)^{\frac{n+1}{2}}} \cdot \int_0^{\infty} y^{\frac{n+1}{2}-1} e^{-y} d y \\ & =\frac{1}{\sqrt{\pi n} \Gamma\left(\frac{n}{2}\right)} \cdot\frac{1}{\left(\frac{t^2}{n}+1\right)^{\frac{n+1}{2}}}\Gamma\left(\frac{n+1}{2}\right) \\ & =\frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{\pi n} \Gamma\left(\frac{n}{2}\right)} \left(\frac{t^2}{n}+1\right)^{-\frac{n+1}{2}}. \end{aligned} \]
Figura 3 de mai jos ilustrează densitatea și funcția de repartiție a unei variabile aleatoare repartizată \(t_n\) unde \(n\in\{1, 3, 9\}\).
Propoziția 5 Arătați că pentru \(n\) suficient de mare avem că \(T\approx \mathcal{N}(0,1)\) (de exemplu observând că, din Legea Numerelor Mari, numitorul tinde la \(1\) atunci când \(n\to\infty\)). Ilustrați grafic acest fenomen.
Demonstrație. Într-adevăr, dacă în limita
\[ \lim _{n \rightarrow \infty}\left(1+\frac{a}{n}\right)^n=e^a, \]
înlocuim pe \(a = x^2\) găsim că
\[ \lim _{n \rightarrow \infty}\left(1+\frac{x^2}{n}\right)^{\frac{n+1}{2}}=e^{\frac{x^2}{2} \lim _{n \rightarrow \infty}\frac{n+1}{n}}=\mathrm{e}^{\frac{x^2}{2}} . \]
În plus, ținând cont de faptul că (acest rezultat se poate obține imediat prin aplicarea inegalității lui Gautschi)
\[ \lim _{n \rightarrow \infty} \frac{\Gamma\left(\frac{n+1}{2}\right)}{\Gamma\left(\frac{n}{2}\right) \sqrt{n}}=\frac{1}{\sqrt{2}} \]
concluzionăm că
\[ \lim _{n \rightarrow \infty}f_n(x)=\lim _{n \rightarrow \infty}\frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{\pi n} \Gamma\left(\frac{n}{2}\right)}\left(1+\frac{x^{2}}{n}\right)^{-\frac{n+1}{2}} = \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}}. \]
Repartiția Fisher-Snedecor
Definiția 3 (Variabilă aleatoare repartizată Fisher-Snedecor) Spunem că o variabilă aleatoare \(F\) este repartizată Fisher-Snedecor (sau pe scurt are repartiția \(F\) sau Fisher) cu \(n_1\) grade de libertate la numărător și \(n_2\) grade de libertate la numitor și notăm \(F\sim F_{n_1,n_2}\) dacă admite densitatea de repartiție
\[ f_{n_{1}, n_{2}}(x)=\frac{\Gamma\left(\frac{n_{1}+n_{2}}{2}\right)}{\Gamma\left(\frac{n_{1}}{2}\right) \Gamma\left(\frac{n_{2}}{2}\right)}\left(\frac{n_{1}}{n_{2}}\right)^{\frac{n_{1}}{2}} \frac{x^{\frac{n_{1}-2}{2}}}{\left(1+\frac{n_{1}}{n_{2}} x\right)^{\frac{n_{1}+n_{2}}{2}}} \quad \text { dacă } x>0 \quad(0 \text { altfel}). \]
Avem următorul de rezultat:
Propoziția 6 (Rezultat de caracterizare a repartiției Fisher) Fie \(U\) o variabilă aleatoare repartizată \(\chi^2_{n_1}\) și \(V\) o variabilă aleatoare repartizată \(\chi^2_{n_2}\), cu \(U\) și \(V\) independente. Atunci variabila aleatoare \(F = \frac{U/n_1}{V/n_2}\) este repartizată Fisher-Snedecor cu \(n_1\) grade de libertate la numărător și \(n_2\) grade de libertate la numitor.
Demonstrație. Vom determina pentru început repartiția comună a vectorului \((F, V)\) și, plecând de la aceasta, vom găsi repartiția marginală a lui \(F\). În acest sens considerăm transformarea
\[ g:(u, v) \mapsto(f, v)=\left(\frac{u/n_1}{v /n_2}, v\right) \]
astfel că \((F,V) = g(U, V)\) și a cărei inversă este dată de
\[ g^{-1}:(f, v) \mapsto\left(\frac{n_1}{n_2}fv, v\right). \]
Matricea Jacobiană corespunzătoare lui \(g^{-1}\) este
\[ J_{g^{-1}}=\left(\begin{array}{cc} \frac{n_1}{n_2}v & \frac{n_1}{n_2}f \\ 0 & 1 \end{array}\right) \]
de unde găsim determinantul \(\operatorname{det}\left(J_{g^{-1}}(f, v)\right)=\frac{n_1}{n_2}v\). Cum \(U\) și \(V\) sunt independente rezultă că densitatea comună a vectorului \((U,V)\) este egală cu produsul densităților marginale,
\[ f_{U, V}(u, v)=f_U(u) f_V(v)=\frac{1}{2^{\frac{n_1}{2}} \Gamma\left(\frac{n_1}{2}\right)} u^{\frac{n_1}{2}-1} e^{-\frac{u}{2}}\frac{1}{2^{\frac{n_2}{2}} \Gamma\left(\frac{n_2}{2}\right)} v^{\frac{n_2}{2}-1} e^{-\frac{v}{2}} \]
prin urmare densitatea comună a vectorului \((F,V)\) este, pentru \(f, v > 0\),
\[ \begin{aligned} f_{F, V}(f, v) & =f_{U, V}\left(g^{-1}(f, v)\right)\left|\operatorname{det}\left(J_{g-1}(f, v)\right)\right|=f_{U, V}\left(\frac{n_1}{n_2}fv, v\right) \frac{n_1}{n_2}v\\ & =\frac{1}{2^{\frac{n_1+n_2}{2}} \Gamma\left(\frac{n_1}{2}\right)\Gamma\left(\frac{n_2}{2}\right)} \left(\frac{n_1}{n_2}\right)^{\frac{n_1}{2}-1} f^{\frac{n_1}{2}-1} v^{\frac{n_1+n_2}{2}-2} e^{-\frac{v}{2}\left(\frac{n_1}{n_2}f + 1\right)}\frac{n_1}{n_2}v\\ & =\frac{1}{2^{\frac{n_1+n_2}{2}} \Gamma\left(\frac{n_1}{2}\right)\Gamma\left(\frac{n_2}{2}\right)} \left(\frac{n_1}{n_2}\right)^{\frac{n_1}{2}} f^{\frac{n_1}{2}-1} v^{\frac{n_1+n_2}{2}-1} e^{-\frac{v}{2}\left(\frac{n_1}{n_2}f + 1\right)}. \end{aligned} \]
Integrând densitatea comună după \(v\) găsim că densitatea marginală a lui \(F\) este
\[ \begin{aligned} f_F(f) &= \int_0^{\infty} f_{F, V}(f, v) dv \\ &= \frac{1}{2^{\frac{n_1+n_2}{2}} \Gamma\left(\frac{n_1}{2}\right)\Gamma\left(\frac{n_2}{2}\right)} \left(\frac{n_1}{n_2}\right)^{\frac{n_1}{2}} f^{\frac{n_1}{2}-1} \int_0^{\infty} v^{\frac{n_1+n_2}{2}-1} e^{-\frac{v}{2}\left(\frac{n_1}{n_2}f + 1\right)} dv \end{aligned} \]
și considerând schimbarea de variabilă \(y = \frac{v}{2}\left(\frac{n_1}{n_2}f + 1\right)\) găsim \(v = \frac{2y}{\frac{n_1}{n_2}f + 1}\) de unde \(d v = \frac{2}{\frac{n_1}{n_2}f + 1} d y\), \(y\in[0,\infty)\) ceea ce conduce la
\[ \begin{aligned} f_F(f) & =\frac{\left(\frac{n_1}{n_2}\right)^{\frac{n_1}{2}} f^{\frac{n_1}{2}-1}}{2^{\frac{n_1+n_2}{2}} \Gamma\left(\frac{n_1}{2}\right)\Gamma\left(\frac{n_2}{2}\right)} \left(\frac{2}{\frac{n_1}{n_2}f + 1}\right)^{\frac{n_1+n_2}{2}-1}\frac{2}{\frac{n_1}{n_2}f + 1}\int_0^{\infty}y^{\frac{n_1+n_2}{2}-1}e^{-y}dy\\ & = \frac{\left(\frac{n_1}{n_2}\right)^{\frac{n_1}{2}} \Gamma(\frac{n_1 + n_2}{2})}{ \Gamma\left(\frac{n_1}{2}\right)\Gamma\left(\frac{n_2}{2}\right)}\cdot \frac{f^{\frac{n_1}{2}-1}}{\left(\frac{n_1}{n_2}f + 1\right)^{\frac{n_1+n_2}{2}}}. \end{aligned} \]
Ca aplicație fundamentală a acestui rezultat avem:
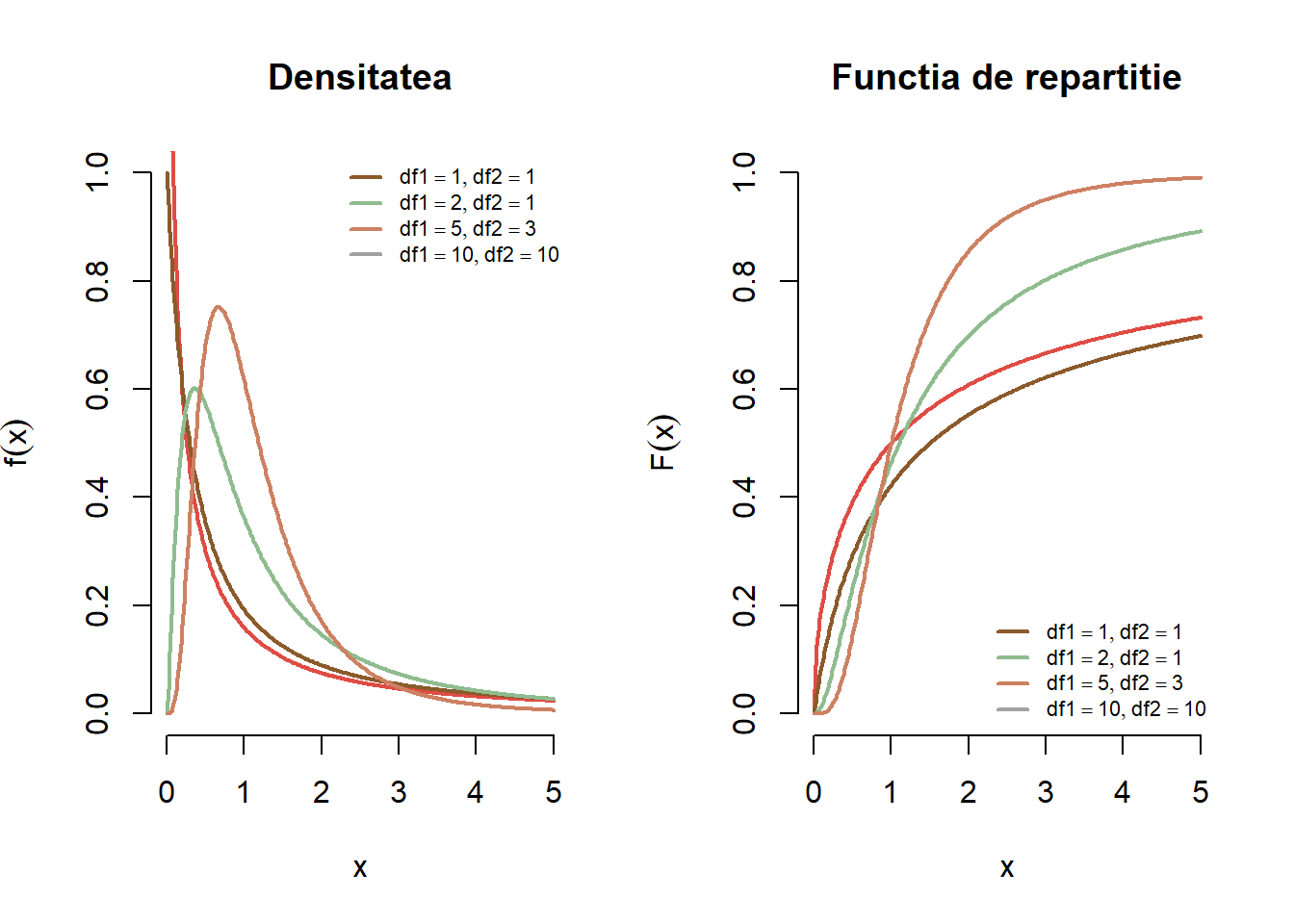
Figura 5 de mai jos ilustrează densitatea și funcția de repartiție a unei variabile aleatoare repartizată \(F_{n_1,n_2}\) pentru fiecare pereche de parametrii \((n_1,n_2)\) din mulțimea \(\{(1,1), (2, 1), (5, 3), (10,10)\}\).
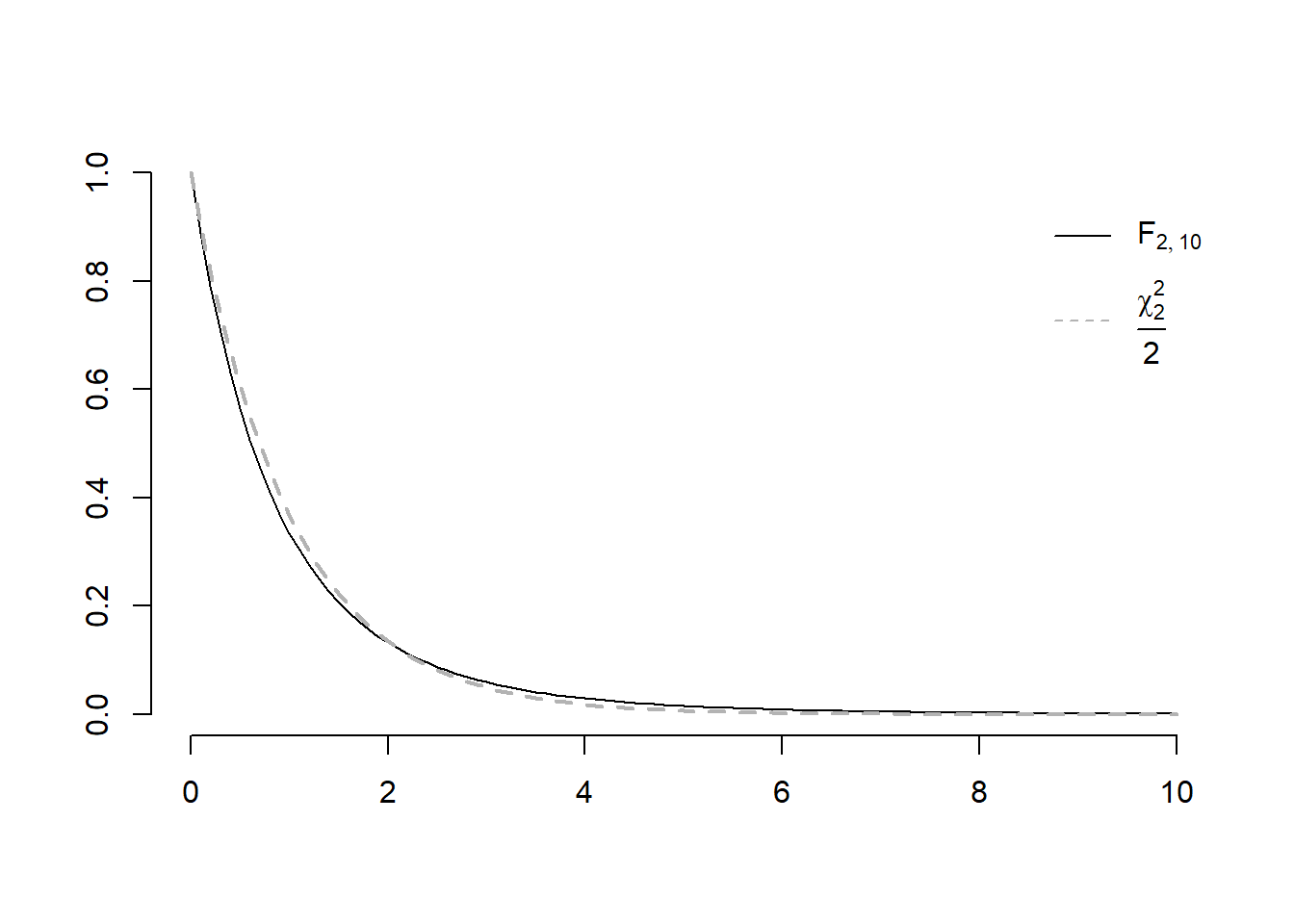
În plus, dacă \(n_2\) este mare atunci putem aproxima repartiția lui \(F\) cu \(F\approx \frac{\chi^2_{n_1}}{n_1}\).