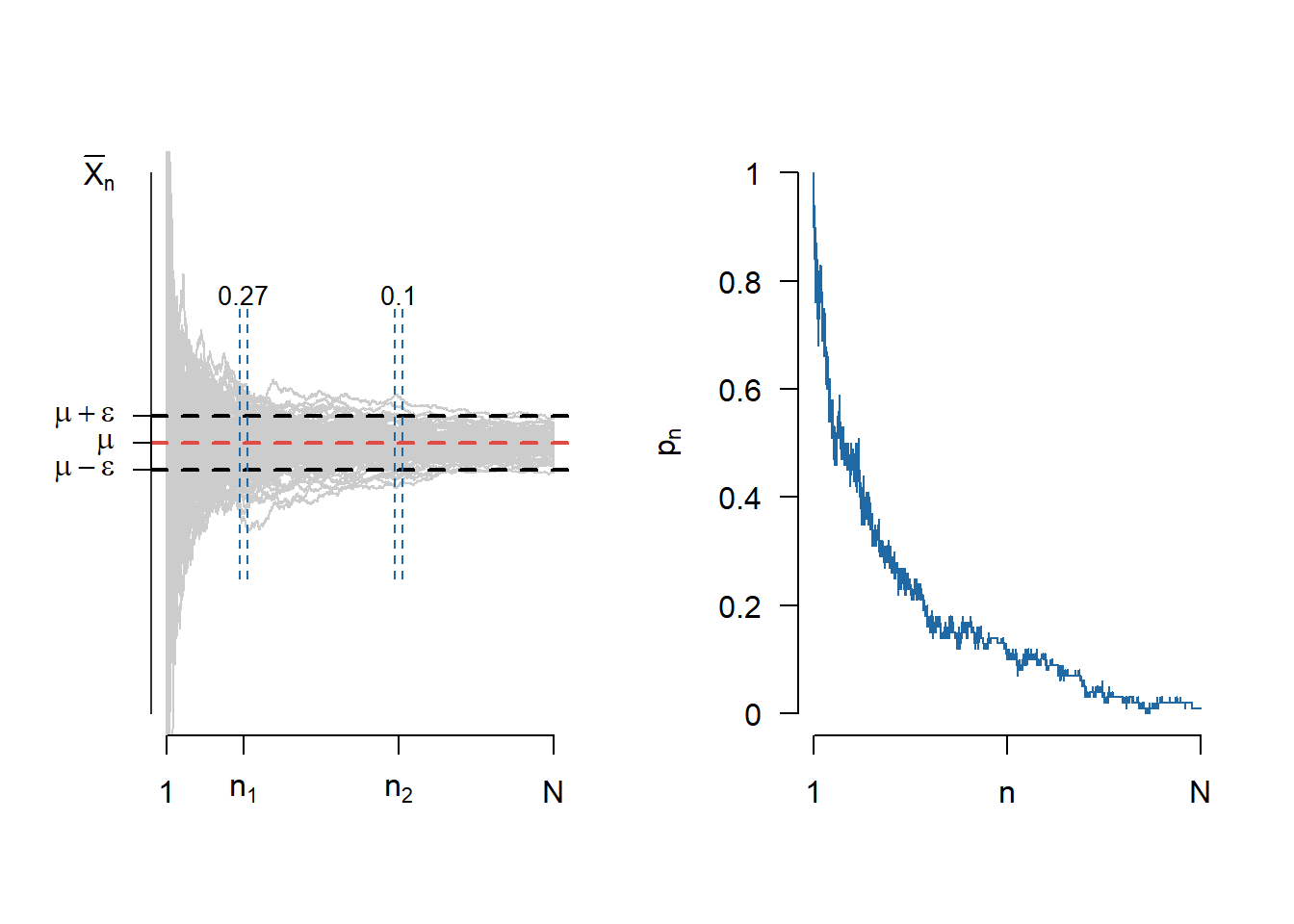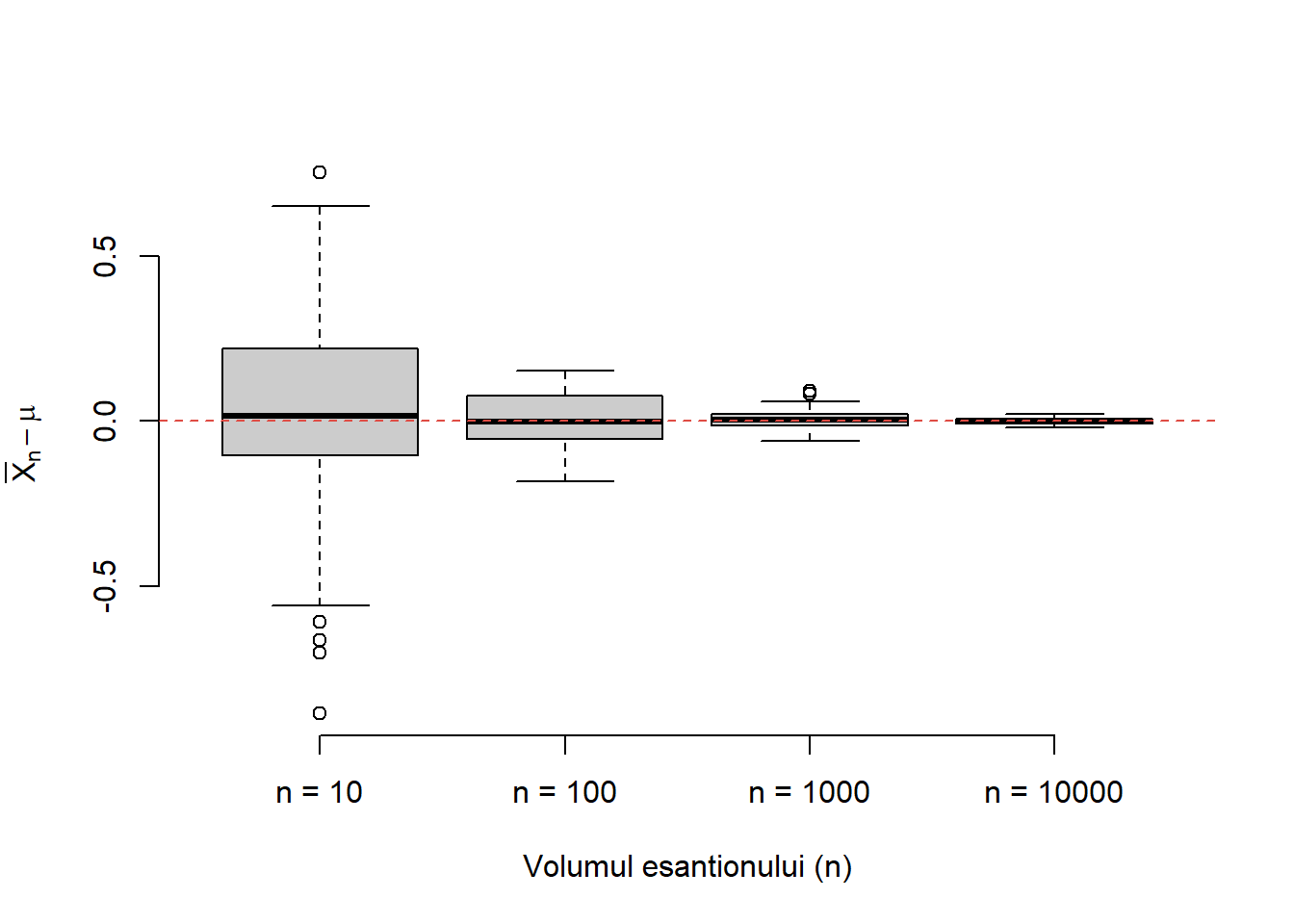În aceste note întroducem două dintre principalele rezultate de probabilități: Legea Numerelor Mari și Teorema Limită Centrală.
1 Legea Numerelor Mari
Înainte de a discuta despre Legea Numerelor Mari este bine să reamintim și să încercăm să înțelegem la nivel intuitiv noțiunea de convergență în probabilitate.
Fie \(X_n, n\geq 1\) și \(X\) variabile aleatoare definite pe câmpul de probabilitate \((\Omega, \mathcal{F}, \mathbb{P})\). Spunem că un șirul de variabile aleatoare \((X_n)_n\) converge în probabilitate la variabila aleatoare \(X\), și notăm \(X_n\overset{\mathbb{P}}{\to}X\), dacă pentru orice \(\epsilon>0\) are loc
\[ \mathbb{P}\left(\left|X_{n} - X\right| > \epsilon\right) \overset{n\to\infty}{\longrightarrow} 0. \]
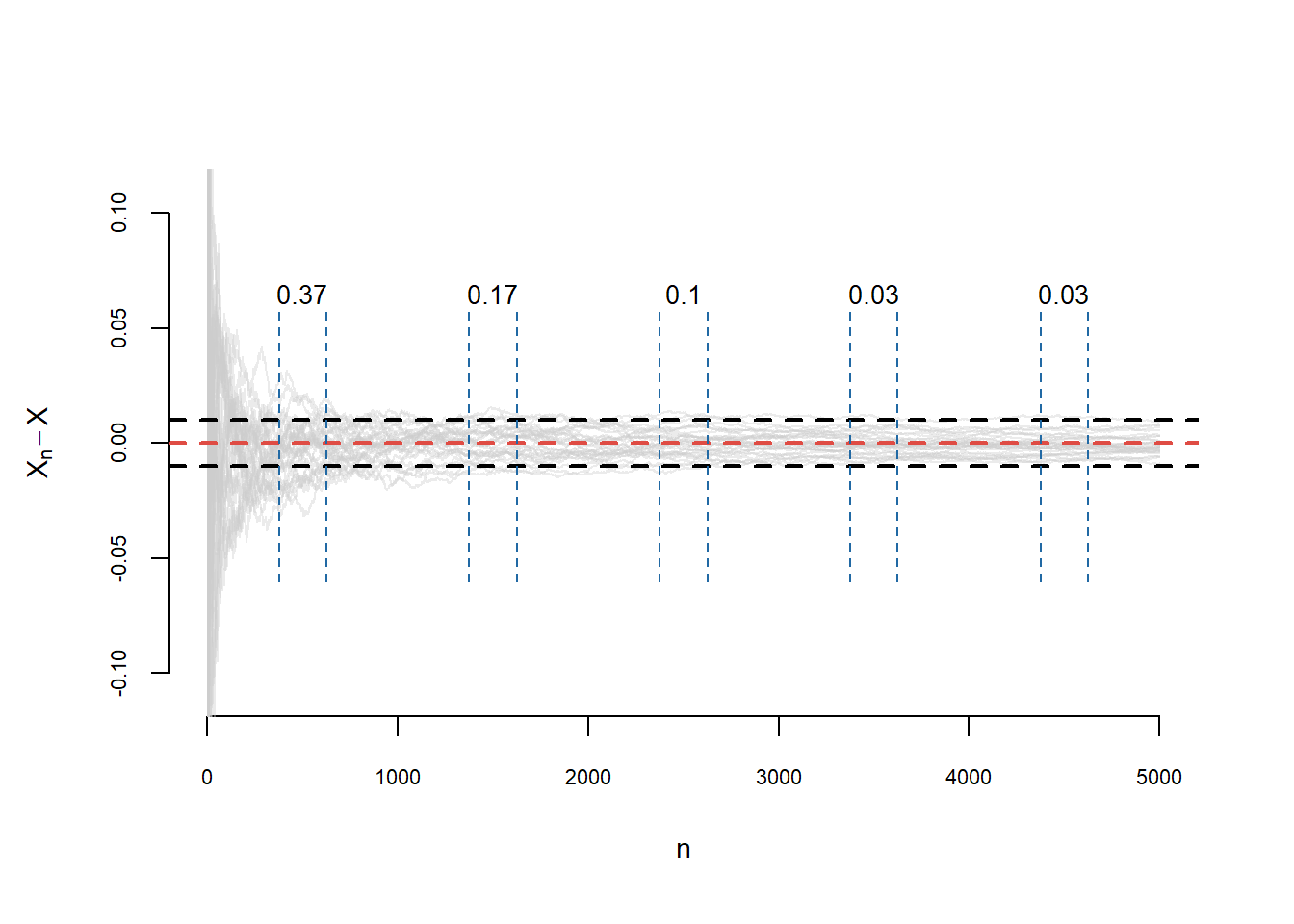
De asemenea putem observa că \(X_n\overset{\mathbb{P}}{\to}X\) dacă și numai dacă \(X_n-X\overset{\mathbb{P}}{\to}0\). Pentru a ilustra grafic acest tip de convergență1 vom aproxima probabilitatea \(\mathbb{P}(A_n)\), unde \(A_n = \{\omega\in\Omega\,|\,\left|X_{n}(\omega) - X(\omega)\right| > \epsilon\}\), folosind abordarea frecvenționistă. Aceasta presupune ca pentru \(n\) dat să considerăm \(\omega_1, \ldots,\omega_M\in\Omega\), \(M\) realizări ale experimentului (repetat în condiții identice) și să folosim aproximarea
\[ \mathbb{P}(A_n) \approx p_n(M) = \frac{\#\left\{j\in\{1,\ldots,M\}\,|\,\left|X_{n}(\omega_j) - X(\omega_j)\right| > \epsilon\right\}}{M}. \]
Concret, în Figura 1.1, considerăm \(M = 30\) de repetiții ale experimentului (avem \(M\) curbe) cu \(n = 5000\) de realizări ale unui șir de variabile aleatoare \(X_k = \frac{Y_1+\cdots+Y_k}{k}\), cu \(Y_i\) independente și repartizate \(\mathcal{U}[0,1]\), \(X = 0.5\) și \(\epsilon = 0.01\). Pentru \(i\in\{500, 1500, 2500, 3500, 4500\}\) am calculat și afișat frecvența de realizarea a evenimentului \(A_i\) (câte din cele \(M\) curbe sunt în afara benzii \([-\epsilon, \epsilon]\) pentru \(i\), fixat). Observăm că \(p_{500}(30) = 0.37\) și \(p_{3500}(30) = 0.03\), convergența lui \(p_n(M)\underset{n\to \infty}{\longrightarrow} 0\) implicând convergența în probabilitate.
Teorema 1.1 (Legea numerelor mari (versiunea slabă)) Fie \(X_1, X_2, \ldots\) un șir de variabile aleatoare independente și identic repartizate, de medie \(\mathbb{E}[X_1] = \mu<\infty\) și varianță \(Var(X_1) = \sigma^2<\infty\). Atunci \(\forall \epsilon>0\) avem
\[ \mathbb{P}\left(\left|\frac{X_1+\cdots+X_n}{n} - \mu\right| > \epsilon\right) \overset{n\to\infty}{\longrightarrow} 0 \]
sau echivalent
\[ \mathbb{P}\left(\left|\frac{X_1+\cdots+X_n}{n} - \mu\right| \leq \epsilon\right) \overset{n\to\infty}{\longrightarrow} 1 \]
Notând media eșantionului cu \(\bar{X}_n = \frac{X_1+\cdots X_n}{n}\), Legea numerelor mari (versiunea slabă) afirmă că \(\bar{X}_n\overset{\mathbb{P}}{\to}\mu\). Figura 1.2 de mai jos ilustrează această convergență pentru \(M = 100\) de traiectorii. În figura din dreapta este ilustrată evoluția probabilității \(p_n\) pentru \(n\in\{1,2,\ldots, N\}\).
Exercițiul 1.1 Să presupunem că primim o monedă și ni se spune că aceasta aterizează pe fața cap în \(48\%\) din cazuri. Vrem să testăm această afirmație. Folosind Legea numerelor mari și știind că vrem să fim siguri în \(95\%\) din cazuri, ne întrebăm de câte ori trebuie să aruncăm moneda pentru a verifica afirmația?
Să presupunem că aruncăm moneda, independent, de \(n\) ori și fie \(X_i\) rezultatul obținut la cea de-a \(i\)-a aruncare: \(X_i=1\) dacă la a \(i\)-a aruncare am obținut cap și \(X_i = 0\) dacă am obținut pajură. Avem că variabilele aleatoare \(X_1, X_2, \ldots, X_n\) sunt independente și repartizare \(\mathcal{B}(p)\), cu \(p=0.48\) din ipoteză.
De asemenea, observăm că \(\mathbb{E}[X_1]= \mu = 0.48\) și \(Var(X_1) = \sigma^2 = p(1-p) = 0.2496\). Pentru testarea monedei permitem o eroare \(\epsilon = 0.02\) ceea ce înseamnă că probabilitatea ca moneda să aterizeze cap se află în intervalul \((0.46, 0.5)\). Din Inegalitatea lui Cebîșev avem că
\[ \mathbb{P}\left(\left|\frac{X_1+\cdots+X_n}{n} - 0.48\right| >0.02\right)\leq \frac{Var(X_1)}{n\times(0.02)^2}, \]
de unde, având un grad de încredere de \(95\%\), vrem să determinăm pe \(n\) pentru care
\[ \frac{0.2496}{n\times(0.02)^2} = 0.05 \]
ceea ce implică \(n = 12480\).
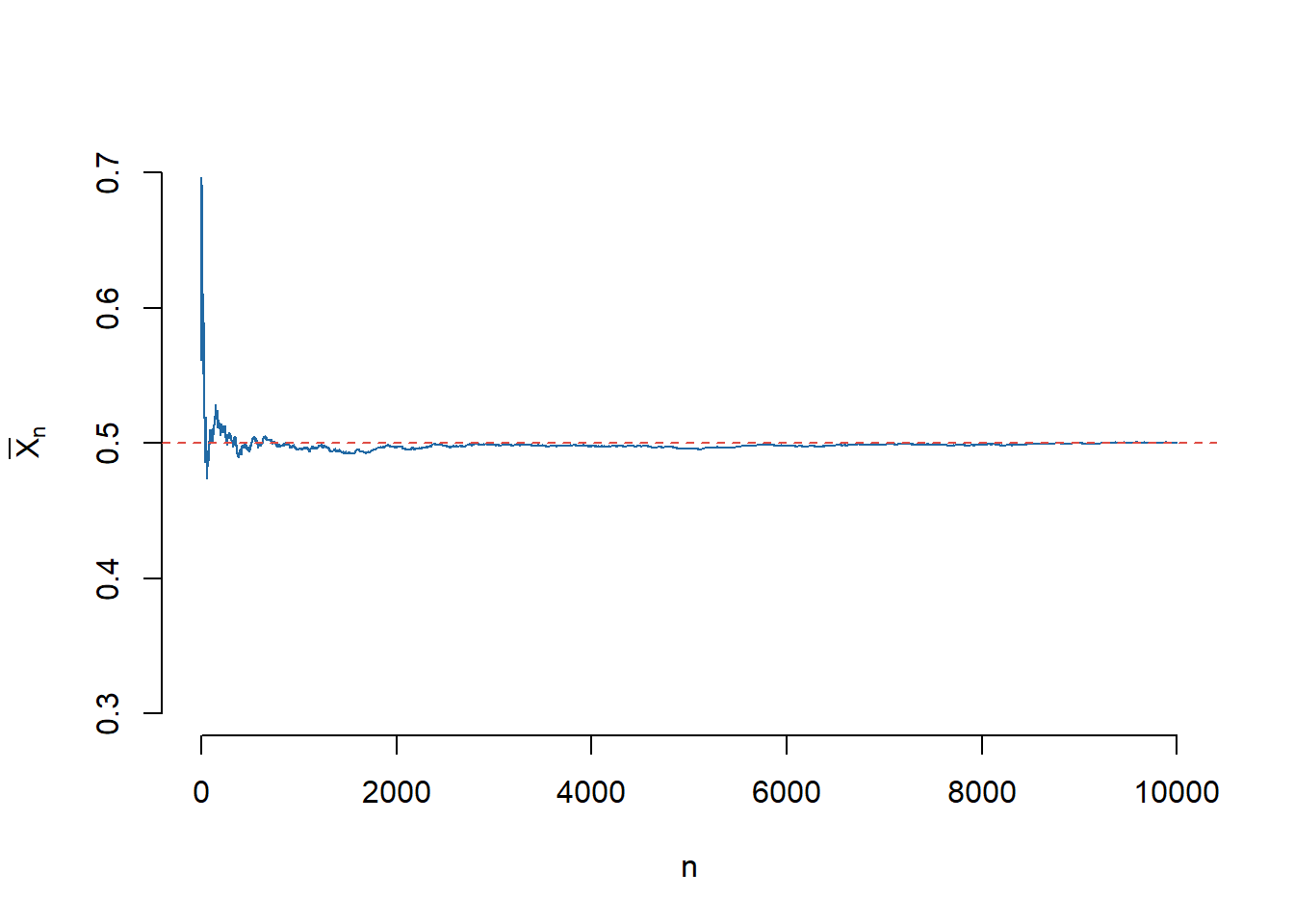
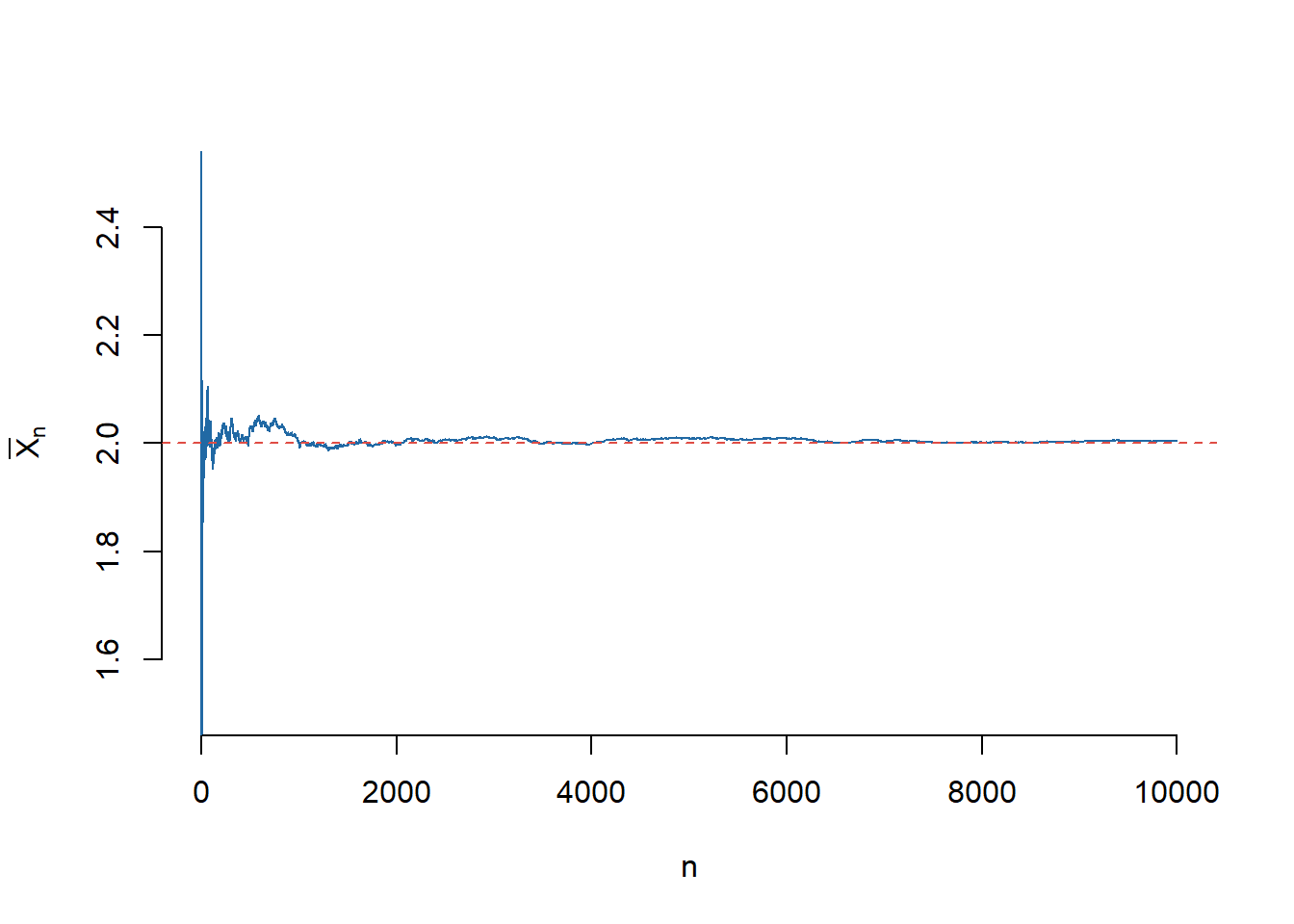
Exercițiul 1.2 (Ilustrarea Legii Numerelor Mari (I)) Fie \(X_1,X_2,\dots,X_N\), \(N\) v.a. i.i.d. de lege \(\mathcal{U}([0,1])\). Pentru \(1\leq n\leq N\), notăm cu \(S_n=X_1+X_2+\cdots X_n\) șirul sumelor parțiale și \(\mu\) media legii \(\mathcal{U}([0,1])\). Trasați pe același grafic funcția \(n\to \bar{X}_n=\frac{S_n}{n}\) pentru \(n=1,\dots,N\) și dreapta de ecuație \(y=\mu\). Faceți același lucru pentru legea normală \(\mathcal{N}(2,1)\).
În cazul în care v.a. \(X_1,X_2,\dots,X_N\) sunt repartizate uniform \(\mathcal{U}([0,1])\) (deci media este \(\mu=\frac{1}{2}\)) avem:
În cazul în care v.a. \(X_1,X_2,\dots,X_N\) sunt normale de parametrii \(\mathcal{N}(2,1)\) (deci media este \(\mu=2\)) avem:
Exercițiul 1.3 (Ilustrarea Legii Numerelor Mari (II)) Construiți o funcție care să vă permită generarea a \(m\) eșantioane de volum \(n\) dintr-o populație normală de medie \(\mu\) și varianță \(\sigma^2\) dată. Ilustrați grafic cu ajutorul unui boxplot cum variază diferența dintre media aritmetică (media eșantionului \(\bar{X}_n\)) și media teoretică pentru \(m = 100\) și diferite volume ale eșantionului \(n\in\{10, 100, 1000, 10000\}\). Se consideră \(\mu = 1\) și \(\sigma^2 = 1\).
Următoarea funcție verifică cerința din problemă (normal.mean = \(\mu\), normal.sd = \(\sigma\), num.samp = m și samp.size = n). Să observăm că am folosit funcția rowMeans pentru a calcula media fiecărui eșantion (media pe liniile matricii de observații).
normalSampleMean <- function(normal.mean, normal.sd, num.samp, samp.size) {
# generam matricea de observatii
x <- matrix(rnorm(n = num.samp * samp.size, mean = normal.mean, sd = normal.sd),
nrow = num.samp, ncol = samp.size)
# calculam media esantionului pentru fiecare esantion
x.mean = rowMeans(x)
return(x.mean)
}Pentru a ilustra grafic să considerăm o populație \(\mathcal{N}(1,1)\) și pentru volumul eșantionului, \(n\in\{10, 100, 1000, 10000\}\), să calculăm \(\bar{X}_n\) corespunzător (aici am folosit funcția sapply).
Din boxplot-ul din Figura 1.5 observăm că pe măsură ce creștem volumul eșantionului media boxplot-ului se duce spre \(0\) ceea ce justifică enunțul Legii Numerelor Mari, și anume că media eșantionului converge la media populației (media teoretică). De asemenea putem observa că și varianța scade (gradul de împrăștiere scade) odată cu creșterea numărului de observații.
Exercițiul 1.4 (Calculul unei integrale (I)) Utilizați Legea Numerelor Mari pentru a aproxima integrala următoare
\[ I = \int_{0}^{1}e^{x}sin(2x)cos(2x)dx. \]
Calculați de asemenea valoarea exactă \(I\) a acesteia și comparați-o cu aproximarea găsită.
Fie \(U_1,U_2,\dots,U_n\) un șir de v.a. i.i.d. repartizare uniform pe \([0,1]\). Cum \(g\) este o funcție continuă atunci \(g(U_1), g(U_2),\ldots, g(U_n)\) sunt variabile aleatoare i.i.d. și aplicând Legea Numerelor Mari obținem
\[ g_n=\frac{1}{n}\sum_{i=1}^{n}g(U_{i}) \overset{\mathbb{P}}{\to} \mathbb{E}[g(U_1)] = \int_{0}^{1}g(x)dx. \]
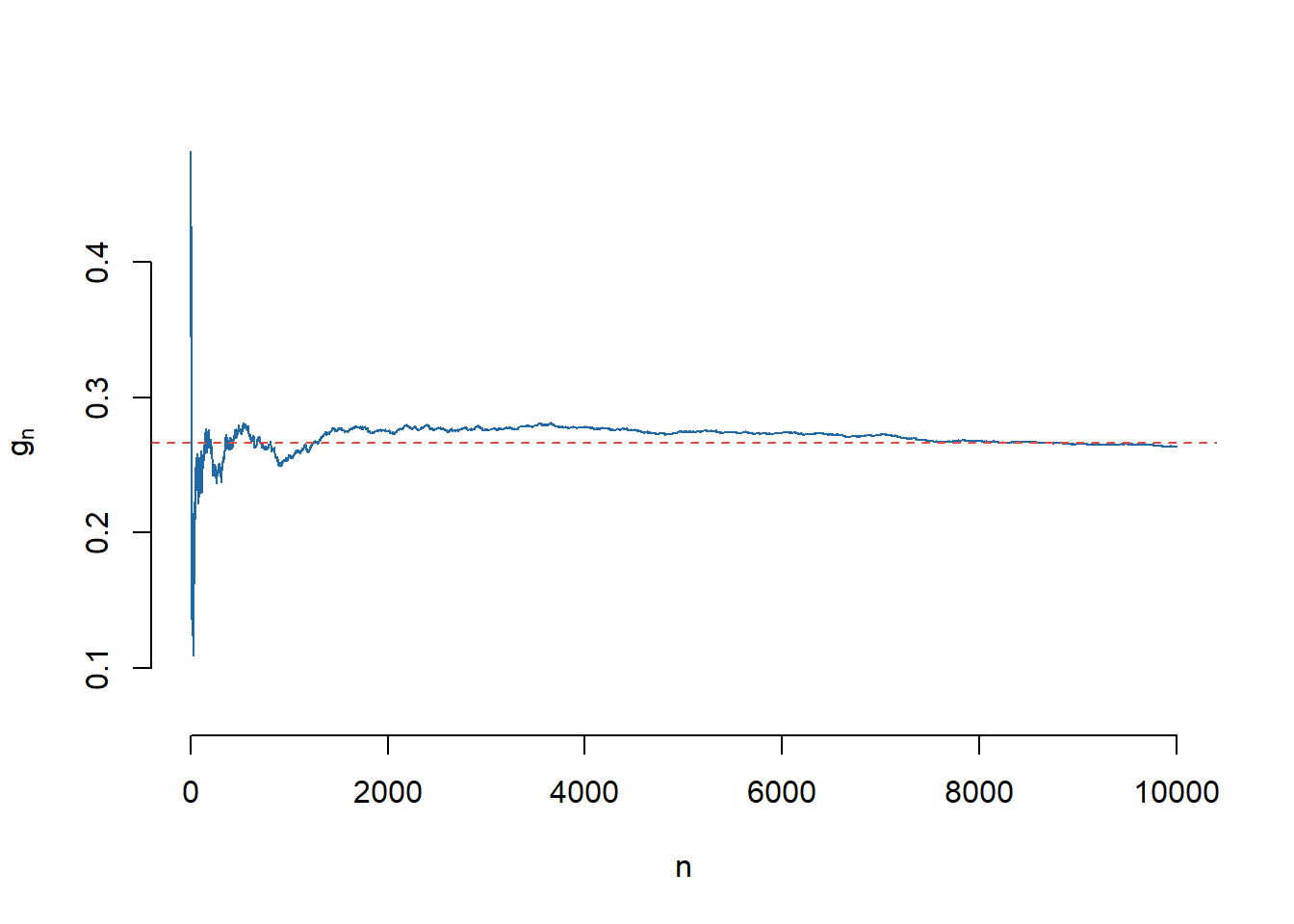
Pentru a calcula integrala numeric vom folosi funcția integrate (trebuie observat că această integrală se poate calcula ușor și exact prin integrare prin părți). Următorul script ne dă valoare numerică și aproximarea obținută cu ajutorul metodei Monte Carlo pentru integrale \(\int_{0}^{1}g(x)dx\):
myfun <- function(x){
y <- exp(x)*sin(2*x)*cos(2*x);
return(y);
}
# calculul integralei cu metode numerice
I <- integrate(myfun,0,1) # raspunsul este o lista si oprim prima valoare
I <- I[[1]]
# calculul integralei cu ajutorul metodei Monte Carlo
n <- 10000
u <- runif(n) # generarea sirului U_n
z <- myfun(u) # calcularea sirului g_n
I2 <- sum(z)/n # aproximarea MCObținem că valoarea numerică a lui \(I\) este 0.2662 iar cea obținută cu ajutorul metodei Monte Carlo este 0.2673.
Avem următoarea ilustrare grafică a convergenței metodei Monte Carlo:
2 Teorema Limită Centrală
Teorema 2.1 (Teorema Limită Centrală) Fie \(X_1, X_2, \ldots\) un șir de variabile aleatoare independente și indentic repartizate, de medie \(\mathbb{E}[X_1] = \mu<\infty\) și varianță \(Var(X_1) = \sigma^2<\infty\). Atunci, notând \(S_n = X_1 + \cdots + X_n\), avem
\[ \mathbb{P}\left(\frac{S_n - \mathbb{E}[S_n]}{\sqrt{Var(S_n)}}\leq x\right) = \mathbb{P}\left(\frac{S_n - n\mu}{\sigma\sqrt{n}}\leq x\right) \overset{n\to\infty}{\longrightarrow} \Phi(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x}e^{-\frac{t^2}{2}}\,dt, \quad \forall x\in\mathbb{R}. \]
Echivalent, dacă notăm media eșantionului cu \(\bar{X}_n = \frac{S_n}{n}\), atunci
\[ \mathbb{P}\left(\sqrt{n}\frac{\bar{X}_n - \mu}{\sigma}\leq x\right) \overset{n\to\infty}{\longrightarrow} \Phi(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x}e^{-\frac{t^2}{2}}\,dt, \quad \forall x\in\mathbb{R}. \]
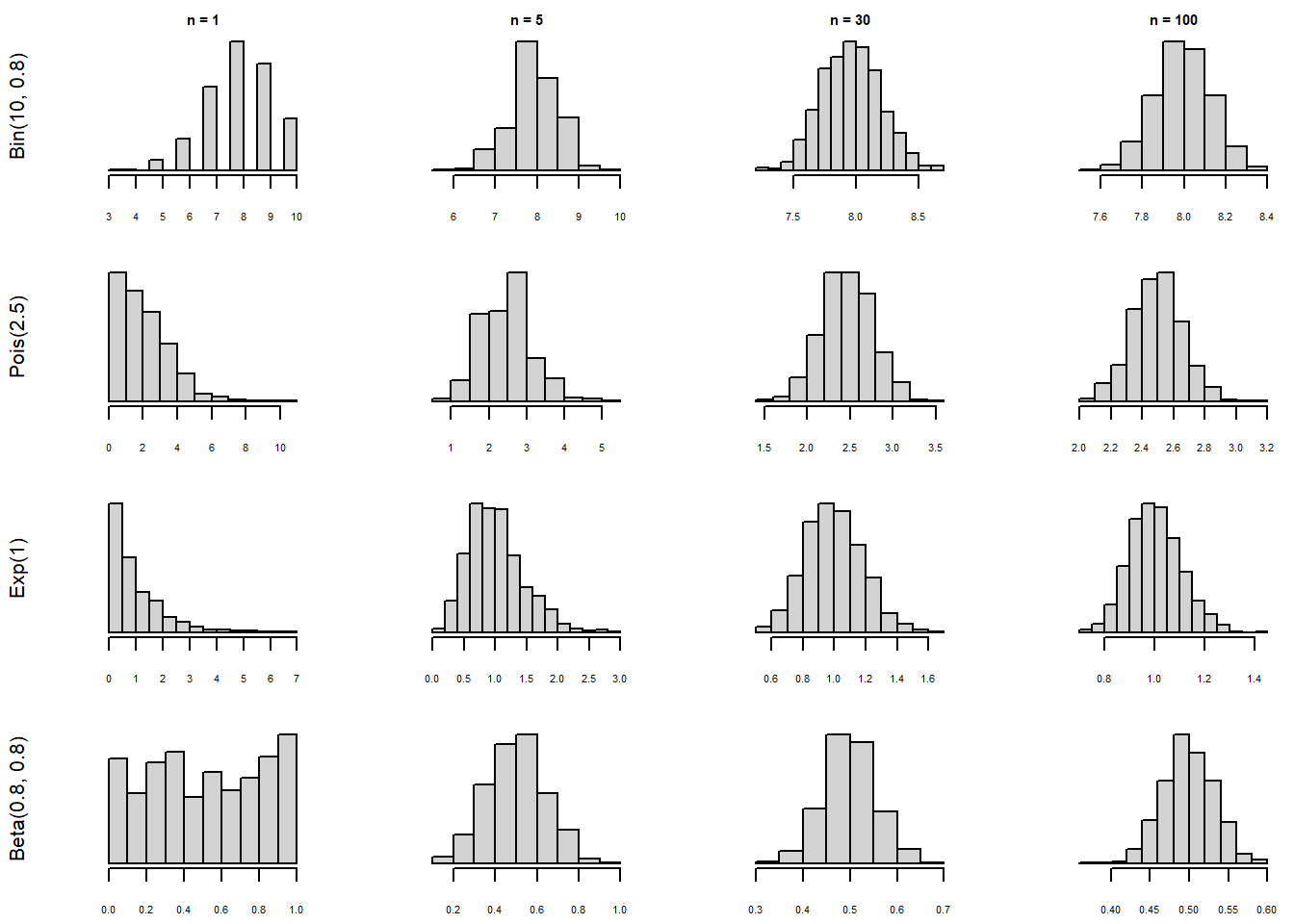
În esență, Teorema Limită Centrală ne spune că, indiferent de repartiția mamă a eșantionului, media eșantionului \(\bar{X}_n\) este aproximativ normal repartizată. În Figura 2.1 de mai jos prezentăm evoluția repartiției lui \(\bar{X}_n\) după volumul eșantionului pentru diferite repartiții inițiale:
O aplicație simplă a Teoremei Limită Centrale este dat de următorul exercițiu:
Exercițiul 2.1 Să presupunem că primim o monedă și ni se spune că aceasta aterizează pe fața cap în \(48\%\) din cazuri. Vrem să testăm această afirmație. Folosind Teorema Limită Centrală și știind că vrem să fim siguri în \(95\%\) din cazuri, ne întrebăm de câte ori trebuie să aruncăm moneda pentru a verifica afirmația? Comparați răspunsul cu cel din exercițiul în care am folosit LNM, de mai sus.
Folosind aceleași notații ca și în exercițiul din secțiunea de mai sus și notând în plus \(S_n = X_1+\cdots+X_n\), avem
\[\begin{align*} \mathbb{P}\left(\frac{S_n}{n}<0.5\right) &= \mathbb{P}\left(\frac{S_n - n\mu}{\sigma\sqrt{n}}<\frac{(0.5-\mu)\sqrt{n}}{\sigma}\right)= \mathbb{P}\left(\frac{S_n - n\mu}{\sigma\sqrt{n}}<\frac{0.02\sqrt{n}}{\sqrt{0.2496}}\right) \\ &= \mathbb{P}\left(\frac{S_n - n\mu}{\sigma\sqrt{n}}<0.04\sqrt{n}\right) \approx\Phi(0.04\sqrt{n})\geq 0.95 \end{align*}\]Prin urmare, \((0.04\sqrt{n}\geq 1.645\) de unde \(n = 1692\). Putem observa că rezultatul obținut prin aplicarea Teoremei Limită Centrală este mai precis decât cel obținut prin aplicarea Legii numerelor mari.
Exercițiul 2.2 Fie \((X_n)_{n\geq1}\) un șir de v.a. i.i.d. de lege \(\mathcal{E}(1)\). Pentru toți \(n\), notăm cu \(S_n=X_1+X_2+\cdots X_n\) șirul sumelor parțiale, \(\mu\) și \(\sigma^2\) reprezentând media și respectiv varianța legii \(\mathcal{E}(1)\). Teorema Limită Centrală afirmă că dacă \(n\) este mare atunci v.a.
\[ \frac{S_n-n\mu}{\sqrt{n}\sigma} \]
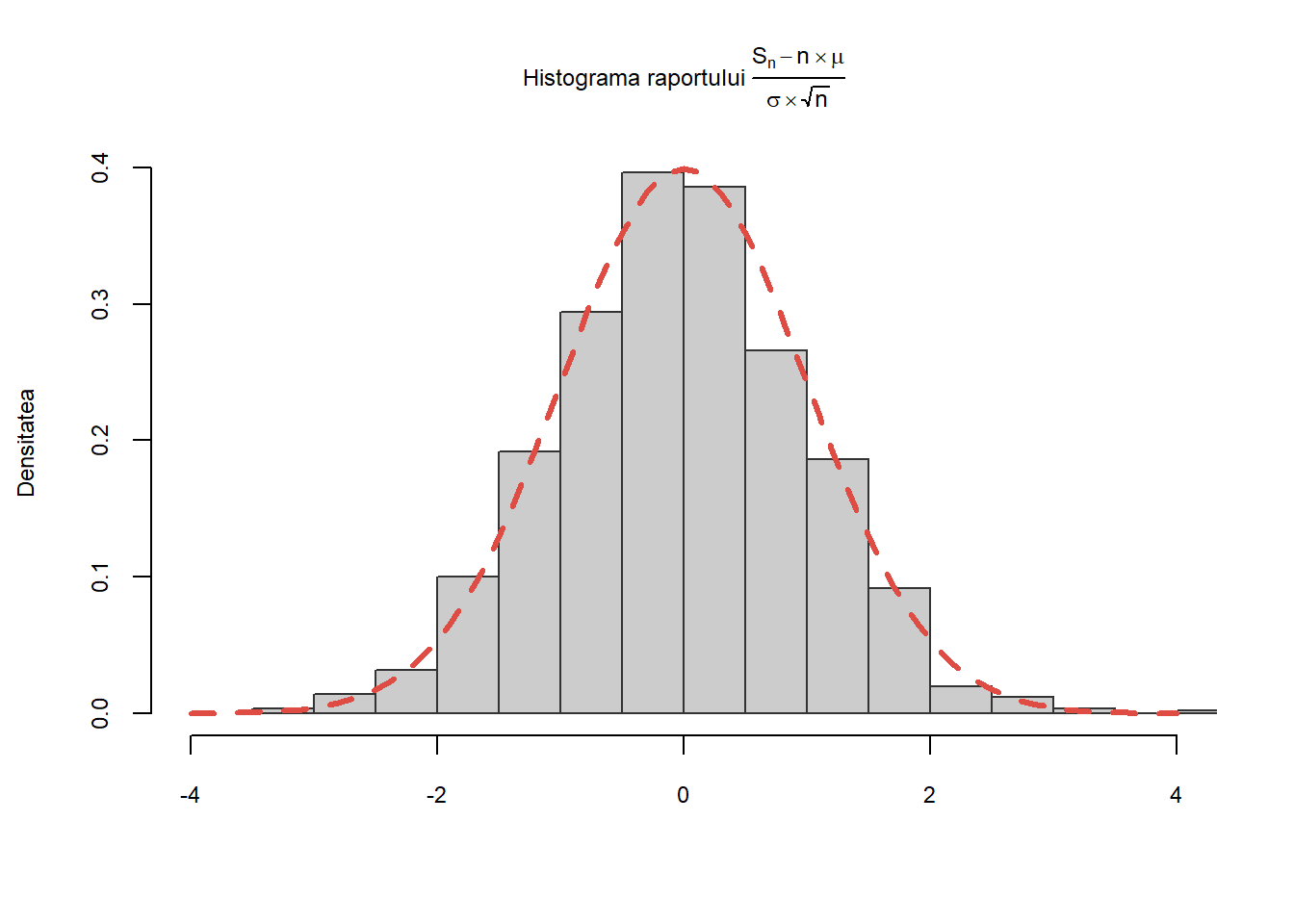
are aproximativ aceeași distribuție ca și legea normală \(\mathcal{N}(0,1)\). Ilustrați această convergență în distribuție cu ajutorul unei histograme. Suprapuneți peste această histogramă densitatea legii \(\mathcal{N}(0,1)\).
Știm că media unei v.a. distribuite exponențial de parametru \(\lambda\), \(\mathcal{E}(\lambda)\) este \(\mu=\frac{1}{\lambda}\) iar varianța acesteia este \(\sigma^2=\frac{1}{\lambda^2}\). Pentru fiecare valoare a lui \(i\) de la \(1\) la \(N\) calculăm raportul \(\frac{S_n-n\mu}{\sigma\sqrt{n}}\) (cu alte cuvinte repetăm experimentul de \(N\) ori):
N <- 1000 # alegem numarul de repetitii ale experimentului
n <- 1000 # alegem n pentru care folosim aproximarea normala
lambda <- 1 # parametrul legii E(1)
mu <- 1/lambda # media
sigma <- 1/lambda # abaterea standard
s <- rep(0,N) # initializam sirul sumelor partiale
for (i in 1:N){
x <- rexp(n, rate = lambda) # generam variabilele exponentiale
s[i] <- (sum(x)-n*mu)/(sigma*sqrt(n)) # calculam raportul
}Continuăm prin trasarea histogramei cerute și adăugăm la grafic densitatea legii normale \(\mathcal{N}(0,1)\):
Note de subsol
Pentru alte moduri de convergență și ilustrarea lor grafică se poate consulta lucrarea: Pierre LAFAYE DE MICHEAUX și Benoit LIQUET Understanding Convergence Concepts: A Visual-Minded and Graphical Simulation-Based Approach, The American Statistician, Vol. 63, No. 2, 2009↩︎